Probing entanglement of Gaussian states
Quantifying entanglement of Gaussian thermal states with 2- and 4-body correlation functions
Related publication: V. Gondret, C. Lamirault,R. Dias, C. Leprince, C.I. Westbrook, D. Clément & D. Boiron. Quantifying two-mode entanglement of bosonic Gaussian states from their full counting statistics. Phys. Rev. Lett. 135, 100201 (2025) PDF or HTML. See also this talk, this poster or the Chapter 2 of my thesis.
Summary
 Quantum entanglement—Einstein’s “spooky action at a distance”—is key to quantum technologies. Measuring it directly tells us how useful a quantum state is for tasks like quantum teleportation. But detecting entanglement typically involves complex and time-consuming measurements, such as mixing modes in an interferometer.
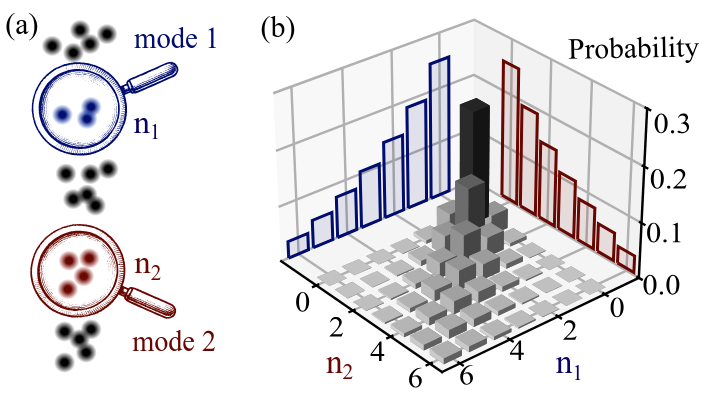
Instead, we use a simpler approach valid for a large class of states known as Gaussian states. For such states, entanglement between two quantum modes can be quantified by simply counting particles to compute the joint probability distribution of particle numbers in each mode—delimited by the lenses on the scheme. This gives the second- and fourth-order correlation functions, which are enough to quantify entanglement.
Quantum entanglement—Einstein’s “spooky action at a distance”—is key to quantum technologies. Measuring it directly tells us how useful a quantum state is for tasks like quantum teleportation. But detecting entanglement typically involves complex and time-consuming measurements, such as mixing modes in an interferometer.
Instead, we use a simpler approach valid for a large class of states known as Gaussian states. For such states, entanglement between two quantum modes can be quantified by simply counting particles to compute the joint probability distribution of particle numbers in each mode—delimited by the lenses on the scheme. This gives the second- and fourth-order correlation functions, which are enough to quantify entanglement.
This method can be applied to two mode Gaussian states of bosons, which are routinely prepared in laboratories. In this scenario, even if the particle number in each mode fluctuates significantly, the difference between the two modes can be surprisingly stable, revealing hidden quantum correlations. This unusual link between entanglement and particle number measurement stems from a special property of Gaussian states: they are entirely described by their first and second statistical moments.
Thanks to advances in single-particle detectors, which can now resolve up to a hundred particles per mode, this result has real experimental impact. To quantify entanglement, experimentalists can simply prepare many realizations of their quantum state and count.
An entanglement criterion for certan kind of two-mode Gaussian states
In general, entanglement cannot be access simply by measuring particle number probability distribution. This only gives access to the diagonal terms of the density matrix while entanglement is typically encoded in the off-diagonal terms. However, some specific states are so constraints that their diagonal gives information about off-diagonal terms. This is the case typically of Gaussian states for example, which are solely defined by their mean value of the field and their two-field correlations (the covariance matrix). This means that two-body correlation functions, which is a four-field correlation function, is expressed as a function of one- and two-field correlation functions.
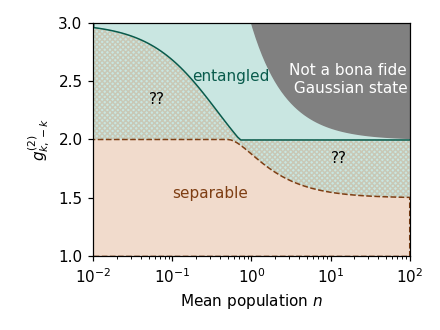
Criterion—In this work, we focus on a subclass of two-mode Gaussian states which are commonly prepared in experiments. We show that for these states, entanglement can be probed by measuring the population in each mode and the cross two- and four body correlation functions. Furthermore, we connect these measurements to logarithm negativity, an entanglement quantifier.
Witness—If instead one only measures the two-body correlation and the population, entanglement can still be assessed. We derive an entanglement threshold above which the state is entangled, no matter the value of the four-body correlation. This threshold is shown as a blue dotted line in the figure. This entanglement witness reveals entanglement in a series of recent experiments.