Along my mathematical carrier I have studied several essentially independent questions; yet these questions share several common features which are related to my mathematical tastes. The title of my Ph.D. thesis, "Some questions in probability theory viewed with a physical twist", sums up these common fetures:
Consider a reversible discrete Markov chain whose transitions must follow the edges of an (unoriented) graph. The motion of this chain is controlled by a Guassian bound due to Carne in 1985:
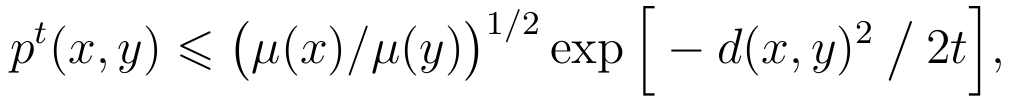
where pt(x,y) is the probability that a chain starting from x will be in y at time t, μ(·) is the equilibrium measure of the reversible chain, and d(·,·) is the graph distance.
As Carne's proof used arguments of spectral theory whose deep meaning was rather unclear, I aimed at getting back his result thanks to a more "natural", probabilistically meaningful method. To do this, I consider an R-valued process depending on the chain's state, and I study that process thanks to martingale theory: my argument is rather close to the forward / backward martingale decomposition of Lyons and Zheng. Using that method, not only one finds Carne's bound again, but also one can generalize the bound to cases where the chain does not necessarily follow the graph's edged —which did not work with spectral theory.
Boltzmann's equation describes the global behaviour of the molecules of a gas, which molecules interact by collisions, when the number of particles becomes infinite. A crucial question consists in knowing to which point that limit is a good approximation of the reality when the number of particles is large, but not infinite. Here we are interested in the spatially homogeneous case —for which the particle model is stochastic. Then, the question is an example of mean field limit problem. Such problems have been studied, among others, by A-S. Sznitman and S. Méléard.
I my work, I put the stress in a uniform, quantitative, non-asymptotic approach. Such an approach is less powerful mathematically, but more relevant as far as physics and simulation are concerned. One of my contributions was to show that it is worth studying the distances between measures in "large" Hilbert spaces rather than e.g. Wasserstein spaces. Indeed, such large Hilbert spaces lead to Gaussian-like convergence results [with a Gaussian control valid up to medium deviations], which is impossible for Wp distances. My method to prove the mean field limit is general and thus likely to apply to other situations.
Ising's model is a model of statistical mechanics modelizing a ferromagnetic material. In this model, in the subcritical regime, two distinct atoms have corelated states, but that correlation decreases (exponentially) with the distance between the atoms. The same phenomenon occurs for a wide range of similar models.
For these models, I got interested in bounding the correlation, not between two individual spins, but between two bunches of spins with possibly infinite sizes. It turns out that in this frame, it is important to know how correlation is measured:
In terms of β-mixing, it is easy enough to prove that there is no decorrelation estimate which would be uniform in the size of the spin bunches. On the other hand, I have shown that it is possible to "tensorize" ρ-mixing to get deccoraltion between infinite bunches of spins. That tensorization result can be stated in a very general framework.
Also, I studied how the idea of tensorization could be applied to get spatial central limit theorems, and also spectral gap for the Glauber dynamics. Though, concerning classical models, my results are not new, they point out a direct Hilbertian approach to these phenomena. An interesting feature of this approach is that it highlights a universal decorrelation hypothesis, which is stated in terms of ρ-mixing.
Besides, I answered a conjecture stated by R. Bradley in 1985 about getting ρ-mixing estimates from decorrelation results on events. The question was the following: let X and Y be two random variables such that, for some ε ∈ (0,1), for all measurable sets A and B:
![P[(X,Y)\in A\times B] - P[X\in A] \times P[Y\in B] \leq \epsilon \times \sqrt{P[X\in A] \times P[Y\in B] \times P[X\notin A] \times P[Y\notin B]}](lambda-mixing.png)
then, is there a bound on the ρ-mixing coefficient between X and Y? It was already known that a bound of the form Cε(|log ε|+1) stood true (with C = 52 in 2010) ; I proved that one could take C = 1 and that then the bound was optimal.
We consider the McKean-Vlasov equation on Rd, which models the evolution of a dense assembly of particles evolving under two kinds of forces (in presence of strong friction):
My aim is to study this phase transition phenomenon beyond its linearized expansion. More precisely, I want to work directly in the space naturally associated to the McKean-Vlasov equation: this space is the nonlinear space of the Wasserstein W2 metric. To do this, I link this space with Sobolev spaces (which are linear indeed). By this method, I prove a nonlocal version of the phase transition in a rather general case. Moreover, I get an explicit lower bound for the activation energy in the supercritical regime.
As I have handled several works involving optimal transportation distances, I have become a kind of (limited!) expert on this topic; so that sometimes some colleagues asked for my help about it. In particular, to answer a question by Xavier Tolsa, I have written a short article in which I state certain non-asymptotic relations that exist between the quadratic Wasserstein distance W2 and the homogeneous Sobolev norm Ḣ−1 (these being known to be formally equivalent for infinitesimally small perturbations), and a way to apply these relations to prove efficiently a &lquo;localisation&rquo; phenomenon for the quadratic Wasserstein distance: namely, if μ and ν are two mass distributions close to each other in the sens of W2 distance, and that φ is a smooth compactly supported function, then one can bound above the W2 distance between (μ · φ) / ||μ · φ|| and (ν · φ) / ||ν · φ|| by some multiple of W2 (μ, ν).
In the &lquo;basic&rquo; model for financial mathematics, no-arbitrage imposes that the assets' prices are semimartingales. Yet one can deal with more general random price processes, including in particular fractional Brownian motion, if there are transaction costs (say, proportional). Walter Schachermayer is one of the mathematicians working on these models with propotional transaction costs; he aims at understanding wht the optimal trading strategy is when your goal is to maximise some expected utility.
I proved that fractional Brownian motion satisfies the &lquo;two-way crossing&dquo; property: namely, you cannot find a stopping time (however cleverly you choose it) after which there would be a positive probability that the fractional Brownian motion would go locally upwards (resp. downwards). By answering this question, which had been open for a few years, we (W. Schachermayer, C. Czichowsky, J. Yang and myself) could show that, when trading a financial asset whose price undergoing a (geometric) fractional Brownian motion, looking for optimising a logarithmic utility, the optimal strategy admits a &lquo;shadow price&dquo;, thanks to which one has a better understanding of that strategy.
→ article on the “two-way crossing” property
→ pre-publication on an application to the existence of a shadow price
Following a question of my colleague Aurélien Moncomble, researcher in chemistry, we found that optimal transportation distances were a relevant way to quantify whether an electronic transition inside a molecule is “charge transfer” or not. To be able to use optimal transportation distances in chemical situations, I had to implement a tool to compute these distances on the data produced by chemists. I named this tool CUBETRANSPORT.