|
Bentley-Otmann Algorithm 2.0
An implementation of Bentley-Ottmann algorithm in order to count the m,n-cubes
|
|
Bentley-Otmann Algorithm 2.0
An implementation of Bentley-Ottmann algorithm in order to count the m,n-cubes
|
This project implements Bentley-Ottmann's algorithm. For a set of segment lines, it computes and returns all the intersections of segment lines of this set. In order to do that, we use the generalized algorithm given in M.de Berg, 0.Cheong, M.van Kreveld and M.Overmars, Computational Geometry: Algorithms and Applications, Third Edition.
This algorithm is based on the principle of sweeping line. We sweep a line from the left to the right (in some papers, it can be found from the top to the bottom) in the 2D plan. At every position of the line, the intersections on the left of the line has been computed and those on the right are waiting to be treated. The interesting positions for the sweeping line are the endpoints of the segment lines of the set and the crossing points. We call those points events.
We treat each event in a natural way :
(Of course, a single event can be of more than one type.)
In order to realize that, we have to maintain two structures : one which gives the presently involved segment (those which are crossing the sweeping line) called the Y-structure and one giving the next event at every time called the X-structure. Since we want to compute all the intersections with a time complexity 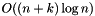 with
with 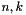 respectively the number of segments and the number of intersections, we have to compute all the actions on the X,Y-structures with a time complexity
respectively the number of segments and the number of intersections, we have to compute all the actions on the X,Y-structures with a time complexity 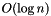 . Naturally, we choose to work with some trees. The X-structure is a priority queue determining the next event at every time. For some algorithmic reasons (we want to be able to know if an object is a member of the X-structure in a logarithmic way), we will use a binary search tree with the lexographic order on the (x,y)-coordinates of the events. For the Y-structure, a binary search tree is a natural choice to order the segment, insert and remove them.
. Naturally, we choose to work with some trees. The X-structure is a priority queue determining the next event at every time. For some algorithmic reasons (we want to be able to know if an object is a member of the X-structure in a logarithmic way), we will use a binary search tree with the lexographic order on the (x,y)-coordinates of the events. For the Y-structure, a binary search tree is a natural choice to order the segment, insert and remove them.
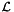 the set of segment having the current event as left endpoints. (We suppose that this set is stored with the event to keep our time complexity.)
the set of segment having the current event as left endpoints. (We suppose that this set is stored with the event to keep our time complexity.) 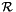 , which is the set of the segment lines having the event point as right endpoint, and
, which is the set of the segment lines having the event point as right endpoint, and 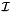 , which is the set of those strictly containing the event point.
, which is the set of those strictly containing the event point. 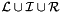 contains strictly more than one element, we can report one intersection.
contains strictly more than one element, we can report one intersection. 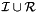 (those from
(those from 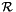 because we does not need them anymore ; those from
because we does not need them anymore ; those from 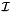 to exchange the order on them when re-inserting)
to exchange the order on them when re-inserting)  :
: 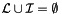 (i.e. the event point was just a right endpoint of some segment lines, but was no left endpoint nor crossing point), then we find s and s' the segment immediately above and below the event point and check for any intersection between them ; if there is one greather than the current event and not already in the events's queue, then we push it.
(i.e. the event point was just a right endpoint of some segment lines, but was no left endpoint nor crossing point), then we find s and s' the segment immediately above and below the event point and check for any intersection between them ; if there is one greather than the current event and not already in the events's queue, then we push it. 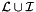 s and the upper one s' ; searching for the below neighboor r of s and the above one r' of s', we check and insert if necessary any new intersection between r and r'.
s and the upper one s' ; searching for the below neighboor r of s and the above one r' of s', we check and insert if necessary any new intersection between r and r'. (Of course, the several researches for neighboors depend of the existence of those neighboors. If they don't, we just have nothing to do relatively to it.)
The files bentley_ottmann.hpp and bentley_ottmann.cpp implement this algorithm. structures.hpp deals with the X,Y-structures using the STL and some customizations. All of that depends of a representation of some geometric objects, what is done in geometry.hpp and geometry.cpp.
 1.7.4
1.7.4