Implementation of Bentley-Ottmann's algorithm. More...

#include "structures.hpp"
#include "geometry.hpp"
#include "bentley_ottmann.hpp"
#include <iostream>
#include <utility>
#include <iterator>
#include <algorithm>

Include dependency graph for bentley_ottmann.cpp:

Go to the source code of this file.

Functions
map_event	bentley_ottmann (std::vector< Segment > &set)
	Computes all the intersections between segment lines of set.
void	find_neighboors (const Point &p, BST< Segment, Point >::Type &btree, Segment &above, Segment &below)
	Find the two neighboors of a point.
Segment *	find_leftmost (vector_seg &v, const Point &p)
	Finds the lower segment.
Segment *	find_rightmost (vector_seg &v, const Point &p)
	Finds the upper segment.
Segment *	find_left_neighboor (Segment *s, BST< Segment, Point >::Type &btree)
	Finds the lower neighboor of a segment in a BST.
Segment *	find_right_neighboor (Segment *s, BST< Segment, Point >::Type &btree)
	Finds the upper neighboor of a segment in a BST.
std::pair< vector_seg, vector_seg >	get_sets (const Point &p, BST< Segment, Point >::Type &btree)
	All segment lines containing a given point.
void	compute_new_events (Segment s0, Segment s1, const Event &p, PriorityQueue< Event, Segment * > &q)
	Compute new events.

Detailed Description

Implementation of Bentley-Ottmann's algorithm.

Author:: Pierre Cagne

Date:: 07/11/2011

This file presents an implementation of Bentley-Ottmann algorithm as shown here.

Definition in file bentley_ottmann.cpp.

Function Documentation

map_event bentley_ottmann ( std::vector< Segment > & set )

Computes all the intersections between segment lines of set.

Parameters:

set	Set of segment lines (implemented as Segment instances)

Returns:: A map_event containing all the event crossing points

Remark : the only Segment instances used are those in set ; to compute the algorithm, we use pointers on Segment-s in order no to copy all those data.

Definition at line 118 of file bentley_ottmann.cpp.

void compute_new_events	(	Segment *	s0,
		Segment *	s1,
		const Event &	p,
		PriorityQueue< Event, Segment * > &	q
	)

Compute new events.

Parameters:

s0,s1	Pointers on segment lines potentially introducing new events.
p	Current event : only events on the right of this one are relevant.
q	Priority queue which into the new events are pushed.

First are checked s0 and s1 for equality to NULL. Next, lazily, s0 and s1 are checked for intersection. Next, lazily again, is checked the intersection to be relevant or not. Finally, the event are pushed into the queue.

Definition at line 357 of file bentley_ottmann.cpp.

Segment* find_left_neighboor	(	Segment *	s,
		BST< Segment, Point >::Type &	btree
	)

Finds the lower neighboor of a segment in a BST.

Parameters:

s	Pointer on the segment whose lower neighboor is wanted.
btree	BST ordering the segment at the given time.

Returns:: Pointer on the lower neighboor of s (if exists, else NULL).

Definition at line 278 of file bentley_ottmann.cpp.

Segment* find_leftmost	(	vector_seg &	v,
		const Point &	p
	)

Finds the lower segment.

Parameters:

v	Non empty vector which for the lower segment is wanted.
p	Point setting the order on segment

Returns:: Pointer on the lower segment in the set.

This is just a classical 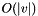$ O(|v|) $ search for minimum in a vector v.

Definition at line 240 of file bentley_ottmann.cpp.

void find_neighboors	(	const Point &	p,
		BST< Segment, Point >::Type &	btree,
		Segment *&	above,
		Segment *&	below
	)

Find the two neighboors of a point.

Parameters:

p	Point that neighboors are searched for.
btree	Binary search tree used to order segments.
above,below	Two pointers use two store the potential neighboors.

This function create a segment of length 0, so a point, anchored in p. In the tree, we search for the upper bound of the segment, getting this way the upper neighboor (if exists). The lower neighboor is now (if exists) the one just before the upper neighboor. That's what this function strictely does.

Definition at line 213 of file bentley_ottmann.cpp.

Segment* find_right_neighboor	(	Segment *	s,
		BST< Segment, Point >::Type &	btree
	)

Finds the upper neighboor of a segment in a BST.

Parameters:

s	Pointer on the segment whose upper neighboor is wanted.
btree	BST ordering the segment at the given time.

Returns:: Pointer on the upper neighboor of s (if exists, else NULL).

Definition at line 292 of file bentley_ottmann.cpp.

Segment* find_rightmost	(	vector_seg &	v,
		const Point &	p
	)

Finds the upper segment.

Parameters:

v	Non empty vector which for the upper segment is wanted.
p	Point setting the order on segment

Returns:: Pointer on the upper segment in the set.

This is just a classical 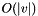$ O(|v|) $ search for maximum in a vector v.

Definition at line 260 of file bentley_ottmann.cpp.

std::pair<vector_seg, vector_seg> get_sets	(	const Point &	p,
		BST< Segment, Point >::Type &	btree
	)

All segment lines containing a given point.

Parameters:

p	Point contained in the wanted segment lines.
btree	BST ordering the segment at the given time.

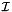Returns:: A pair of vector of segment lines : the first is $\mathcal I$ , the second $\mathcal R$ defined here.

We use here the following trick : we first create a vertical segment line of length 0 anchored in p ; this segment line have a slope of value infinity and so is greather than any segment line going through p except maybe some other vertical segment line containing p ; that kind of vertical segment line is limited to a single element because we do not accept overlapping segment (undefined comportement of the algorithm) ; so having the upper bound of the segment line with length 0 assure us to point on the greatest segment line containing p ; it just remains to back browsing the BST structure because all the segment containing p are adjacent in the tree.

Definition at line 320 of file bentley_ottmann.cpp.

Functions

Detailed Description

Function Documentation