Au cours de ma carrière mathématique, j’ai étudié plusieurs questions essentiellement indépendantes, mais partageant néanmoins plusieurs thèmes fédérateurs liés à ma sensibilité mathématique. Le titre de ma thèse de doctorat, "Quelques problèmes d’inspiration physique en théorie des probabilités", donne une idée de ces thèmes communs :
Soit une chaîne de Markov discrète réversible dont les transitions doivent suivre les arêtes d’un graphe (non orienté). Les déplacements de cette chaîne sont contrôlés par une borne gaussienne établie par Carne en 1985:
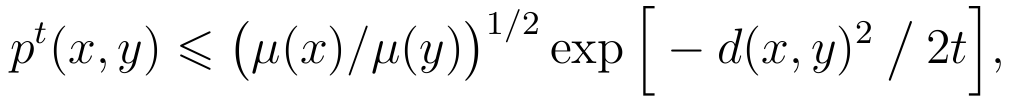
où pt(x,y) est la probabilité que la chaîne issue du point x soit en y au temps t, μ(·) est la mesure d’équilibre de la chaîne réversible, et d(·,·) est la distance du graphe.
Comme la démonstration de Carne utilisait des arguments de théorie spectrale d’interprétation assez mystérieuse, j’ai voulu retrouver son résultat à l’aide d’une méthode plus "naturelle" ayant une signification probabiliste. Pour ce faire, j’ai introduit un processus à valeurs dans R fonction de l’état de la chaîne, que j’ai étudié à l’aide de martingales par un argument assez similaire à la décomposition en martingales forward / backward due à Lyons et Zheng. Ce faisant, non seulement on retrouve la borne de Carne, mais en outre on en montre des généralisations au cas où la chaîne ne suit plus forcément les arêtes du graphe, chose que la théorie spectrale était incapable de faire.
L’équation de Boltzmann décrit le comportement global des molécules d’un gaz interagissant par collisions lorsque le nombre de particules tend vers l’infini. Une question essentielle est de savoir à quel point cette limite approche bien la réalité quand le nombre de particules est grand mais pas infini. On s’intéresse ici au cas de l’équation spatialement homogène : dans ce cas, il s’agit d’un problème de limite de champ moyen, avec un modèle particulaire stochastique. Ce genre de problèmes a été étudié notamment par A-S. Sznitman et par S. Méléard.
Dans mon travail, j’ai mis l’accent sur une approche uniforme, quantitative et non-asymptotique, moins puissante mathématiquement mais plus pertinente pour les questions liées aux situations physiques et à la simulation. Une de mes contributions a été de montrer l’intérêt d’étudier les distances entre mesures dans des espaces de Hilbert « assez gros » plutôt que, par exemple, dans les espaces de Wasserstein, car cela permet d’obtenir une vitesse de convergence de type théorème-limite central [le contrôle gaussien va même jusqu’aux moyennes déviations], chose impossible avec les distances Wp. La méthode que j’ai mise au point pour démontrer la limite de champ moyen dans ce paradigme est générale et susceptible de s’appliquer à d’autres situations.
Le modèle d’Ising est un modèle de physique statistique représentant un matériau ferromagnétique. Dans ce modèle, en régime sous-critique, les états de deux atomes distincts sont corrélés, mais cette corrélation décroît (exponentiellement) avec la distance. Le même phénomène se produit pour un grand nombre de modèles du même genre.
Pour ces modèles, la question que je me suis posée est de borner la corrélation, non pas entre deux spins individuels, mais entre deux groupes de spins de tailles éventuellement infinies. Il s’avère que dans ce cadre, le choix de la façon de mesurer la corrélation a son importance :
En termes de β-mélange, on montre assez facilement qu’il ne peut pas y avoir d’estimation de décorrélation uniforme en la taille des groupes de spins. J’ai démontré que par contre il est possible, dans un cadre très général, de « tensoriser » le ρ-mélange pour obtenir ainsi la décorrélation entre des groupes des spins infinis.
J’ai aussi montré comment l’idée de tensorisation pouvait être appliquée à l’étude du théorème-limite central, et du trou spectral de la dynamique de Glauber. Bien que ces derniers résultats ne disent rien de nouveau concernant les modèles classiques, ils ont le mérite d’indiquer une approche directement hilbertienne de ces phénomènes, par laquelle apparaît une hypothèse universelle de décorrélation qui s’exprime en termes de ρ-mélange.
J’ai par ailleurs résolu une conjecture formulée par R. Bradley en 1985 sur l’obtention d’estimations de ρ-mélange à partir de décorrélations sur les événements. La question était : soient deux v.a. X et Y telles que, pour un ε ∈ (0,1), pour tous ensembles mesurables A et B :
![P[(X,Y)\in A\times B] - P[X\in A] \times P[Y\in B] \leq \epsilon \times \sqrt{P[X\in A] \times P[Y\in B] \times P[X\notin A] \times P[Y\notin B]}](lambda-mixing.png)
comment peut-on alors majorer le ρ-mélange entre X et Y ? Il était connu qu’une borne de la forme Cε(|log ε|+1) convenait (avec C = 52 jusqu’ici) ; j’ai démontré qu’on pouvait prendre C = 1 et que la borne obtenue était alors optimale.
On s’intéresse à l’équation de McKean-Vlasov sur Rd : cette équation modélise l’évolution d’une assemblée dense de particules qui sont soumises, d’une part à un potentiel d’interaction attractif à courte portée qui tend à les regrouper en petits tas, d’autre part à un terme de diffusion qui tend à homogénéiser leur densité (le tout en présence de forts frottements). Sous cette évolution, une transition de phase se produit en fonction de la température : à basse température la distribution homogène est un équilibre instable, alors qu’à haute température cet équilibre devient stable.
Mon objectif est d’étudier ce phénomène de transition de phase au-delà de l’équation linéarisée, en travaillant directement dans l’espace naturellement associé à l’équation de McKean-Vlasov, lequel est l’espace non linéaire de la métrique de Wasserstein W2. Pour ce faire, j’établis des liens entre cet espace et des espaces de Sobolev (qui eux sont linéaires). Je parviens ainsi à démontrer une version non locale de la transition de phase dans un cadre assez général. En outre, je minore explicitement l’énergie d’activation dans le régime où l’équilibre homogène est stable.
Ayant régulièrement été confronté aux distances de transport optimal au cours de mes travaux, j'ai fini par développer une certaine expertise (partielle !) sur ces distances, et il m'est arrivé que des collègues me sollicitent à ce sujet. C'est ainsi que, suite à une sollicitation de Xavier Tolsa, j'ai produit un court article décrivant les relations non asymptotiques qu'on peut établir entre la distance de Wasserstein quadratique W2 et la norme de Sobolev homogène Ḣ−1 (dont on savait qu'elles sont formellement équivalentes pour des perturbations infinitésimales), ainsi que la façon dont on peut utiliser cette connexion pour montrer la &lquo;localisation&rquo; de la distance de Wasserstein quadratique: à savoir, si μ et ν sont deux mesures proches au sens de la distance W2 et que φ est une fonction régulière à support compact, alors on peut borner la distance W2 entre (μ · φ) / ||μ · φ|| et (ν · φ) / ||ν · φ|| par un certain multiple de W2 (μ, ν).
Dans le modèle de référence des mathématiques financières, le contrainte de non-arbitrage impose que les prix des actifs suivent des semimartingales. Il est cependant possible d'appréhender des modèles de prix suivant des processus aléatoires plus généraux, incluant en particulier le mouvement brownien fractionnaire, dès lors qu'on prend en compte des frais de transaction (p. ex. proportionnels). Walter Schachermayer, notamment, étudie beaucoup ces modèles à frais de transaction proportionnels, et cherche en particulier à caractériser la stratégie de trading optimale (optimale au sens de la maximisation d'une fonction d'utilité).
J'ai montré que le mouvement brownien fractionnaire vérifiait la propriété dit de “two-way crossing”: il est impossible de trouver un temps d'arrêt, si malin soit-il, juste après lequel le mouvement brownien fractionnaire aurait une probabilité strictement positive de repartir localement à la hausse (resp. à la baisse). La réponse à cette question, qui était ouverte depuis quelques années, a notamment permis de montrer (dans un travail mené par W. Schachermayer, C. Czichowsky, J. Yang et moi-même) que, lorsqu'on trade un actif suivant un mouvement brownien fractionnaire (géométrique) selon une fonction d'utilité logarithmique, la stratégie optimale est caractérisée par l'existence d'un « prix fantôme » qui permet de mieux comprendre ce que l'on fait.
→ article sur la propriété de “two-way crossing”
→ prépublication sur l'application à l'existence d'un prix fantôme
Contacté par mon collègue chimiste Aurélien Moncomble qui cherchait une façon pertinente de quantifier le caractère à tranfert de charge d'une transition électronique au sein d'une molécule, il nous est apparu que les distances de transport optimal offraient à cette question une réponse adéquate. Afin d'utiliser cet outil pour l'analyse chimique, il m'a fallu implémenter un outil de calcul numérique des distances de transport optimal utilisable sur les jeux de données produits par les chimistes. Cet outil a été mis au point sous le nom de CUBETRANSPORT.