Tutorial 1: Pairwise invasibility plots¶

Biological problem¶

It has been observed that animals seems to present morphological characteristics that seems adapted to their foraging technique. Observing fishes we see deep body shape in the littoral zone and when preying on sedentary benthic prey, predicted to be adaptive since it allows a higher precision in maneuverability (Webb 1984; Domenici 2003). In contrast, a body shape, allowing rapid accelaration is predicted to be beneficial when foraging on planktonic prey (Webb 1984; Domenici 2003).

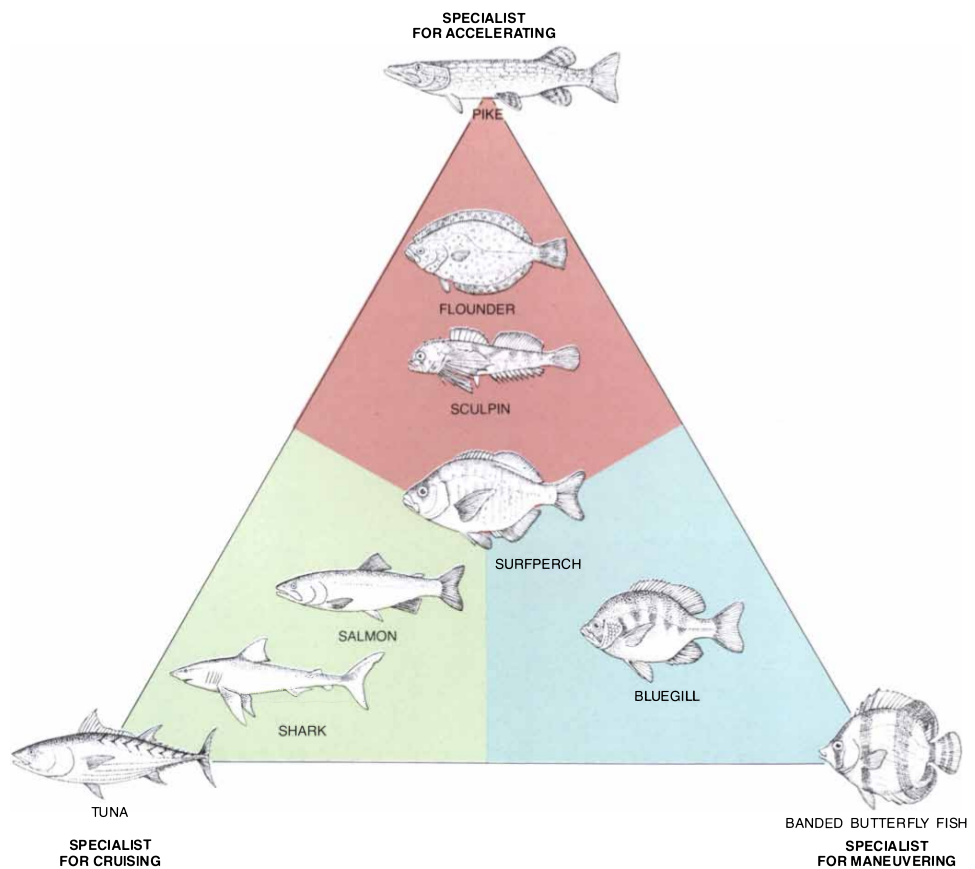
Figure: Functional Morphology Plane (from Webb 1984) Fishes in the corner are specialized for one swimming function.

What are the evolutionary consequence of such a partition of ressource ? Will we see pure strategies evolve (only hunting benthic prey or foraging plankton) or mixed ? Under which conditions ? Could it lead to speciation ?

What will we use to solve this ? Adaptive dynamics ! (of course this is the title of the tutorial).

Reminder of the main hypothesis of adaptive dynamics (Geritz 1992):

We separate ecological and evolutionary timescale by considering that mutations are rare enough so they appear in a monomorphic resident mutation. From there they can either invade or disappear. We are just interested in their ability to invade (measured by invasion fitness, i.e. the exponential growth rate of a rare mutant).

Two important assumptions:

• The resident is at ecological equilibrium.
• The mutant is at low initial density.

Modeling the problem¶

Population dynamics¶

Let us start by modeling the population dynamics. Here is the list of assumptions...

• There is a consumer $N$, and two ressources ($F_1$ and $F_2$) occuring in two habitats.
• Population are unstructered, asexual, big enough to be modeled in $\mathbb R \to \mathbb{R}^3$, $t \mapsto (N(t), F_1(t), F_2(t))$ (continuous time, continuous population, no explicit spacialization).
• Ressource $1$ (resp $2$) follow a Chemostat dynamics with dilution rate $\delta_1$ (resp. $\delta_2$) and carrying capacity $K_1$ (resp. $K_2$). It has been argued (Persson 1998) that it was a realistic model of resources if (1) the resource has a physical refuge, (2) the resource has adult class size that are too small to be eaten (invulnerable) and then grow into vulnerable class size. (Here, doing a rough sketch of $\frac{dN}{dt} = f(N)$ can give a good idea of the qualitative differences between this and the logistic model you are probably more used to).
• Consumers have a per capita birth rate $\beta$ and per capita death $\mu$ rate.

We get to:

\begin{equation*} \begin{cases} \frac{dF_1}{dt} = \delta_1 (K_1 - F_1(t)) & \text{Density of prey in env. 1} \\ \frac{dF_2}{dt} = \delta_2 (K_2 - F_2(t)) & \text{Density of prey in env. 2} \\ \frac{dN}{dt} = (\beta - \mu) N(t) & \text{Density of fish} \end{cases} \end{equation*}

Predator-prey interactions¶

Let us walk through the hypothesis behind the interactions...

• Spacialization is implicit in the interaction terms. No direct interaction between $F_1$ and $F_2$. Consumer have a heritable trait (denoted by $u$) which measure the specialisation for foraging $F_1$.
• Holling Functional response of type 1 (per capita consumption is linear with the prey density). "$- \alpha F_1(t)N(t)$"
• The value of the consumption rate is given by a search-succes rate in a given environment multiplied by the time spent in the environment: $u A_1$ and $(1-u)A_2$
• Empirical evidence suggest that $A_2: u \mapsto A_2(u) = a_2$ is constant (Andersson 2003). We assume that $A_1$ is an afine function of $u$: $u \mapsto A_1(u) = a_1+b_1u$.
• The consumer per capita birth rate is proportional to the consumption rate.

The full model is: \begin{equation*} \begin{cases} \frac{dF_1}{dt} = \delta_1 (K_1 - F_1(t)) - F_1(t)N(t)uA_1(u) & \text{Density of prey in env. 1} \\ \frac{dF_2}{dt} = \delta_2 (K_2 - F_2(t)) - F_2(t)N(t)(1-u)A_2(u) & \text{Density of prey in env. 2} \\ \frac{dN}{dt} = (\beta(u) - \mu) N(t) & \text{Density of fish} \end{cases} \end{equation*}

\begin{equation} \beta(u) = \underbrace{F_1(t)}_{\text{(prey density)}} \underbrace{A_1(u)}_{\text{(search rate)}} \underbrace{u}_{\text{(time spent)}} + \underbrace{F_2(t)}_{\text{(prey density)}} \underbrace{A_2(u)}_{\text{(search rate)}} \underbrace{(1-u)}_{\text{(time spent)}} \end{equation}

Adaptive dynamics framework¶

Now we want to apply our Adaptive dynamics method on the heritable trait $u$. Remember that we need a rare mutant in a stable monomorphic resident population.

We start by adding an equation to the system to add a mutant type. We denote $r$ the resident trait and $m$ the mutant trait.

\begin{align} \begin{cases} \frac{dN_r}{dt} &= (\beta(r) - \mu) N_r(t)\\ \frac{dN_m}{dt} &= (\beta(m) - \mu) N_m(t)\\ \frac{dF_1}{dt} &= \delta_1 (K_1 - F_1(t)) - F_1(t)[ N_r(t)rA_1(r) + N_m(t)mA_1(m) ]\\ \frac{dF_2}{dt} &= \delta_2 (K_1 - F_2(t)) - F_2(t)[ N_r(t)(1-r)A_2(r) + N_m(t)(1-m)A_2(m) ] \end{cases} \end{align}

We can simplify this cumbersome system by eliminating the ressource dynamics with a QSS (Quasy Steady State) approximation (which is coherent with our biological assumption that ressources follow a chemostat dynamics with a faster dynamics than the predator):

\begin{align*} \frac{dF_1}{dt} = \frac{dF_2}{dt} =& 0 \\ \Leftrightarrow& \begin{cases} F_1^*(N_r, N_m) = \frac{\delta_1 K_1}{\delta_1 + N_r(t)rA_1(r) + N_m(t)mA_1(m)} \\ F_2^*(N_r, N_m) = \frac{\delta_2 K_2}{\delta_2 + N_r(t)(1-r)A_2(r) + N_m(t)(1-m)A_2(m)} \\ \end{cases} \end{align*}

Thus the system becomes:

\begin{align} \begin{cases} \frac{dN_r}{dt} &= [\beta(r, N_r(t), N_m(t)) - \mu] N_r(t)\\ \frac{dN_m}{dt} &= [\beta(m, N_r(t), N_m(t)) - \mu] N_m(t)\\ \end{cases} \end{align}

Our goal is to compute the invasion growth rate of a mutant (with trait $m$) in an environment set by a resident (with trait value $r$). We denote this quantity $s_r(m)$.

Now we factor in the assumptions of Adaptive Dynamics (Geritz 1998):

1. The resident is at ecological equilibrium: $\frac{dN_r}{dt} = 0;   N~r~(t) = N^*$;

2. The mutant is at low density: $N_m \approx 0$

$N^*$ is given by solving $\beta(r, N_r(t), N_m(t)) - \mu = 0$ for $N(t)$ with $N_m(t) = 0$.

The invasion fitness $s_r(m)$ is given by:

\begin{align*} s_r(m) =& \beta(m, N^*, 0) - \mu \\ =& F_1(N^*, 0)mA_1(m) + F_2(N^*, 0)(1-m)A_2(1-m)\\ \end{align*}

Note that $s_r(r)=0$ this is an important feature of adaptive dynamics and checking this is a good test to do when you are trying to apply it.

Finding $N^*$ is not trivial, we'll do it numerically. Nevertheless we can have a ballpark estimation by considering that $\delta_1<< A_1(r)N^*$ and $\delta_1<< A_2(r)N^*$:

\begin{align*} \beta(r, N_r(t), N_m(t)) - \mu &= 0\\ \frac{\delta_1 K_1 A_1(r) r}{A_1(r)rN^*+\delta_1} + \frac{\delta_2 K_2 A_2(r) r}{A_2(r)rN^*+\delta_2} - \mu &= 0\\ \frac{\delta_1 K_1 A_1(r) r}{A_1(r)rN^*} + \frac{\delta_2 K_2 A_2(r) r}{A_2(r)rN^*} &\approx \mu\\ \frac{\delta_1 K_1 + \delta_2 K_2}{N^*} &\approx \mu\\\ \frac{\delta_1 K_1 + \delta_2 K_2}{\mu} &\approx N^* \end{align*}

Numerical Pairwise invasibility plot¶

We want to plot the subset of $[0,1]^2$ where:

\begin{equation} s_r(m) > 0 \;\; \text{for} \;\; s,r \in [0,1]^2 \end{equation}

You will need the following functions: scipy.optimize.fsolve, Use the doc to check what they are doing.

Here is a function to get you started.

Exercise Complete the following functions:

Here are some functions to display the pairwise invasibility plot. Re-writing them on your own is a good exercise.

They make use of:

• numpy.linspace,
• numpy.meshgrid,
• matplotlib.pyplot.contourf.
• numpy.frompyfunc

How to read a pip¶

Try to draw the pip for the three example parameter sets.

What do you conclude for the stability of the evolutionary strategy in each case ?

2. Exploring the trade-off¶

How could we explain this ? Here is a clue: it is a trade-off problem. How can we check that mixed strategy fair better or worse than other ? Plotting $(\text{Search rate}) \times (\text{time spent})$ of one environment against the other could be a good idea, try it !

Exploring the branching¶

The case p_strong leads to a singular point which is convergence stable but not evolutionary stable. We predict that this might cause a branching in the population.

Remember how the PIP is interested in how a rare mutant can invade a resident population ? We considered that if the rare mutant per capita growth rate was positive ($s_r(m)$), the mutant would invade. We completely disregard the rest of the invasion dynamics.

There is something easy we can look at though: the end of the invasion dynamics. If a mutant somehow managed to be in high enough proportion so that it is the one at equilibrium, and the resident is in rare proportion, is the mutant able to drive the resident to extinction ?

The answer of course is to look at $s_m(r)$. This can be done by just flipping the PIP along the diagonal (red in the figure).

Now if we superimpose the PIP with its flipped version, we get 3 kinds of zone:

• The mutant increases if rare, the resident decreases if rare (blue).
• The mutant decreases if rare, the resident increases if rare (red).
• Both mutant and resident increase if rare (green).

This last situation is called a protected polymorphism. In this region we predict that the mutant can invade but not exclude the resident leading to a dimorphic population.

One may add the isoclines zero of the polymorphic invasion fitness (cf. main lecture) to find the final position of the branches.