rote_generation.cpp File Reference

Generation of the Rote sequences representing the m,n-cubes of the discrete plans through (0,0,0). More...

#include <iostream>
#include <cstdlib>
#include <CGAL/Cartesian.h>
#include <CGAL/Arr_segment_traits_2.h>
#include <CGAL/Arr_extended_dcel.h>
#include <CGAL/Arrangement_2.h>
#include <CGAL/Gmpz.h>
#include <CGAL/Gmpq.h>
#include <boost/math/common_factor_rt.hpp>
#include <stack>

Go to the source code of this file.

Classes
struct	VertexData
struct	EdgeData
struct	FaceData
Typedefs
typedef CGAL::Gmpz	Integer
typedef CGAL::Gmpq	rat
typedef CGAL::Cartesian< rat >	Kernel
typedef CGAL::Arr_segment_traits_2 < Kernel >	Traits_2
typedef Traits_2::Point_2	Point_2
typedef Traits_2::X_monotone_curve_2	Segment_2
typedef CGAL::Arr_extended_dcel < Traits_2, VertexData, EdgeData, FaceData >	Dcel
typedef CGAL::Arrangement_2 < Traits_2, Dcel >	Arrangement_2
typedef Arrangement_2::Face_handle	Face_ptr
Functions
ostream &	operator<< (ostream &stream, char **matrix)
void	flip (int const &i, int const &j, char **matrix_src, char **matrix_dest)
std::list< Face_ptr >	dfs (Arrangement_2 const &graph, Face_ptr f)
int	main (int argc, char **argv)
Variables
int	m
int	n

---

Detailed Description

Generation of the Rote sequences representing the m,n-cubes of the discrete plans through (0,0,0).

Author:

Pierre Cagne

Date:

08/04/2011

Definition in file rote_generation.cpp.

---

Typedef Documentation

typedef CGAL::Arrangement_2<Traits_2, Dcel> Arrangement_2

Defining the arrangement type.

Definition at line 198 of file rote_generation.cpp.

typedef CGAL::Arr_extended_dcel<Traits_2, VertexData, EdgeData, FaceData> Dcel

DCEL extended : graph with data on his components (vertices, edges, faces).

Definition at line 195 of file rote_generation.cpp.

typedef Arrangement_2::Face_handle Face_ptr

Handle a face. Facility for handling dual graphs.

Definition at line 204 of file rote_generation.cpp.

typedef CGAL::Gmpz Integer

CGAL's arrangements require an exact integer type.

Definition at line 180 of file rote_generation.cpp.

typedef CGAL::Cartesian<rat> Kernel

Compute a geometric kernel for CGAL's facilities.

Definition at line 186 of file rote_generation.cpp.

typedef CGAL::Gmpq rat

All intersections and endpoints are known to be rational.

Definition at line 183 of file rote_generation.cpp.

---

Function Documentation

std::list<Face_ptr> dfs	(	Arrangement_2 const &	graph,
		Face_ptr	f
	)

Depth-first search on the dual graph

graph Primal graph

f Handle for the root face

Returns:

List of Face_ptr performing a depth-first search (and so a spanning tree).

This will compute a depth-first search on the dual graph of graph. This way we visit all the faces (so all the Rote sequence) of the graph only once. Handling a face with some Rote sequence, we can update all its still unvisited neighboor faces. This is the core of the computation, everything else is either purely technical or cosmetic.

Definition at line 244 of file rote_generation.cpp.

void flip	(	int const &	i,
		int const &	j,
		char **	matrix_src,
		char **	matrix_dest
	)

Flip on m,n-cubes

i,j Parametrizing the flip.

matrix_src Source matrix (Rote sequence of a m,n-cube) ; start

for the flip.

matrix_dest Initially full with 0s. Will contain the flip from

matrix_src.

Going from a face to another through an edge with (standing line of) equation 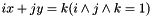will change from 0 to 1 or from 1 to 0 every position 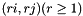of the Rote sequence representing the m,n-cube of the source face.

Definition at line 220 of file rote_generation.cpp.

int main	(	int	argc,
		char **	argv
	)

Main function

int main(int argc, char** argv)

Parameters:

argc,argv

Classic paramters.

Precondition:

argc = 3

argv contains 2 strings, each containing an int.

Violating one of the conditions will exit with a error message.

Might be implement as a function to call in a larger program.

Todo:

Try to set data on edges while inserting segment lines. This would avoid to cover them all after.

Definition at line 286 of file rote_generation.cpp.

ostream& operator<<	(	ostream &	stream,
		char **	matrix
	)

Pretty-print for matrices.

Precondition:

matrix has to be of size .

Returns:

Updated stream.

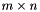Definition at line 169 of file rote_generation.cpp.