m,n-cubes Generator: Main Page

Algorithm

Considering the graph presented in [DJVV08], one can fast generate all the Rote sequences for m,n-cubes of plans through (0,0,0). Here are presented the way to do it.

First, each faces correpond to one and only one such m,n-cube. So, to reach our goal, one have to visite each face at least once (and for more efficiency only once).

Secondly, knowing the Rote sequence of a given face, it is easy to compute the Rote sequence of a neighboor face (i.e. a face sharing an edge with the given one). It is a usefull property. Indeed, randomly scanning the graph's faces, it is really not efficient to track the corresponding m,n-cube per se. So, having this property, the problem is to travel over all the faces, only once, and through the edges : it is the search of a spanning tree. Knowing that the lower most left face corresponds to the flat m,n-cube (i.e. of the Rote sequence the matrix full of 0s), one can perform a depth-first search (or a breadth-first one) to solve the problem. That is indeed what it is done here.

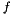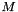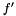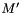Last but not least, let's explain the computing of a new Rote sequence going from a known face to a neighboor other through an edge. Let $ f $ be the known face (i.e. the Rote sequence if the m,n-cube representing by this face is known) and $ M $ the matrix representation of the known Rote sequence. Let $ f' $ and $ M' $ be the homologous unknown ones. Finally, let 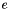$ e $ be the sharing edge (our graph is such that only one edge can be shared by two given bounded faces). 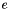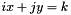Let also the equation of the standing line of $ e $ be : $ ix+jy = k $ .
Then, by construction of the graph, for a plan 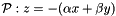$\mathcal P : z = -(\alpha x + \beta y)$ whose dual point is in 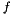$ f $ (let's say 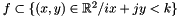$f \subset \{(x,y)\in \mathbb R^2 / ix+jy < k\}$ ), and a plan 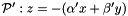$\mathcal P' : z = -(\alpha' x + \beta' y)$ whose dual point is in 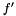$ f' $ (so is 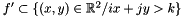$f' \subset \{(x,y)\in \mathbb R^2 / ix+jy > k \}$ ), we have

$\begin{aligned} \forall (p,q) \notin i\mathbb Z \times j\mathbb Z,\ &-\lfloor \alpha p + \beta q \rfloor = -\lfloor \alpha' p + \beta' q \rfloor\\ \forall r \geq 1,\ &-(\lfloor \alpha ri + \beta rj \rfloor +1) = -rk = -\lfloor \alpha' ri + \beta' rj \rfloor \end{aligned}$

So, translating this modulo 2, we have

$\begin{aligned} \forall (p,q) \notin i\mathbb Z \times j\mathbb Z,\ & M_{p,q} = M'_{p,q}\\ \forall r \geq 1,\ & M_{ri,rj} = \overline{M'_{ri,rj}} \end{aligned}$

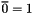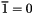where $\overline{0} = 1$ and $\overline{1} = 0$ .

And so, computing a Rote sequence from another going through an edge with equation 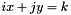$ix+jy=k$ is done by flipping the values in position 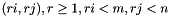$(ri,rj), r \geq 1, ri < m, rj < n$ in the known Rote sequence.

Implementation

In order to implement this algorithm, one have to maintain the structure of the graph while inserting the segment lines. We will here use CGAL (Computational Geometry Algorithms Library) and its module Arrangement_2.
CGAL requires a kernel to do some geometric statements : we will work in the 2D plan with rational (based on GMP) cartesian coordinates. That the meaning of the three first typedef. We then have to deal with the arrangements : the initial structure of arrangement in CGAL is not helpfull in the sense that the vertices, edgesand faces can not contains data (other that the graph's structure). Hopefully, CGAL offers a way to extend them called DCEL extended (Double-Connected Edge List extended). Data in the vertices are irrelevant for us. Data in the edges will be i and j from the equation (see above). Data in the faces will be a Rote sequence (a double entry array of char), and a boolean used in the depth-first search.
We will construct the graph by incremental insertions (that avoids a preliminary stock of the segment lines), then set the data on the edges and finally perform the depth-first search.

The depth-first search is computed on Face_handle (that is kind of a pointer on a face) and does as follows :

Create an empty list of face handlers to return at the end.
Create an empty stack of face handlers, push the root face into it and mark th root face as discovered.
While the stack isn't empty :
- Pop the head, mark it as discovered, and push it into the list.
- For every neighboor face of the head : if not discovered and if bounded, mark as discovered, push it into the stack and flip its Rote sequence from the head's Rote sequence (as shown here).

The dfs function will return a list cointaining the face handlers in a depth-first order.

Let's go : rote_generation.cpp