Jérémie Bettinelli École polytechnique Laboratoire d'informatique (LIX) 91128 Palaiseau Cedex FRANCE E-mail : prenom « . » nom « at » normalesup « . » org Bureau : 2023 Téléphone : (+33) (0)1 77 57 80 61

Sorry, no English version

Passons à l'ordre 4. On cherche les polyèdres du type (3, a, b, c), puisque des considérations immédiates d'angles montrent qu'un des quatre nombres est nécessairement 3 (en effet quatre carrés forment une figure plane).

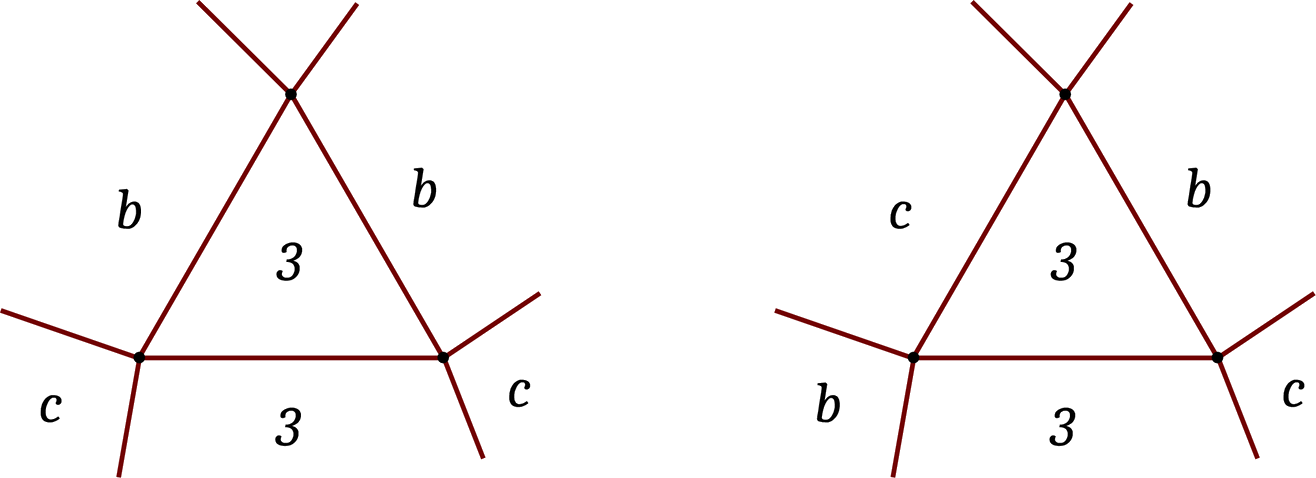Si a＝3, alors on peut supposer que b ≤ c et on obtient que b＝3. En effet, en regardant les deux possibilités pour les sommets du bas sur l'image à droite ci-contre, on obtient ce résultat puisque, parmi les 4 faces incidentes au sommet du haut, au moins 2 doivent être de degré 3.

On obtient ainsi une seconde famille infinie, la famille des antiprismes (3,3,3, n), où n ≥ 3, dont l'octaèdre fait partie.

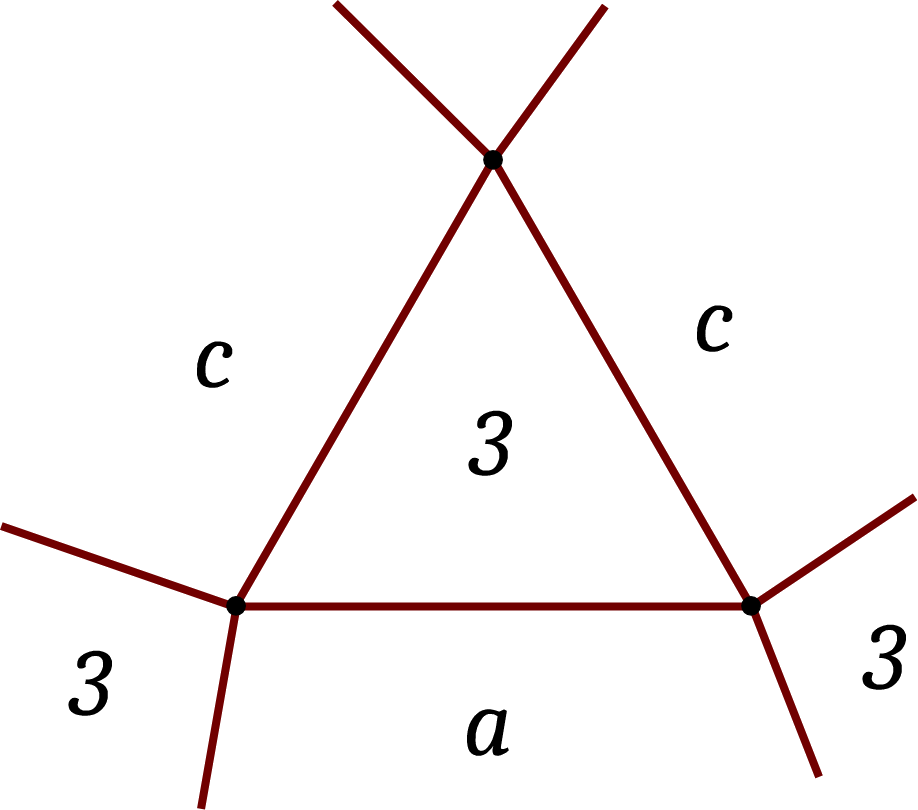
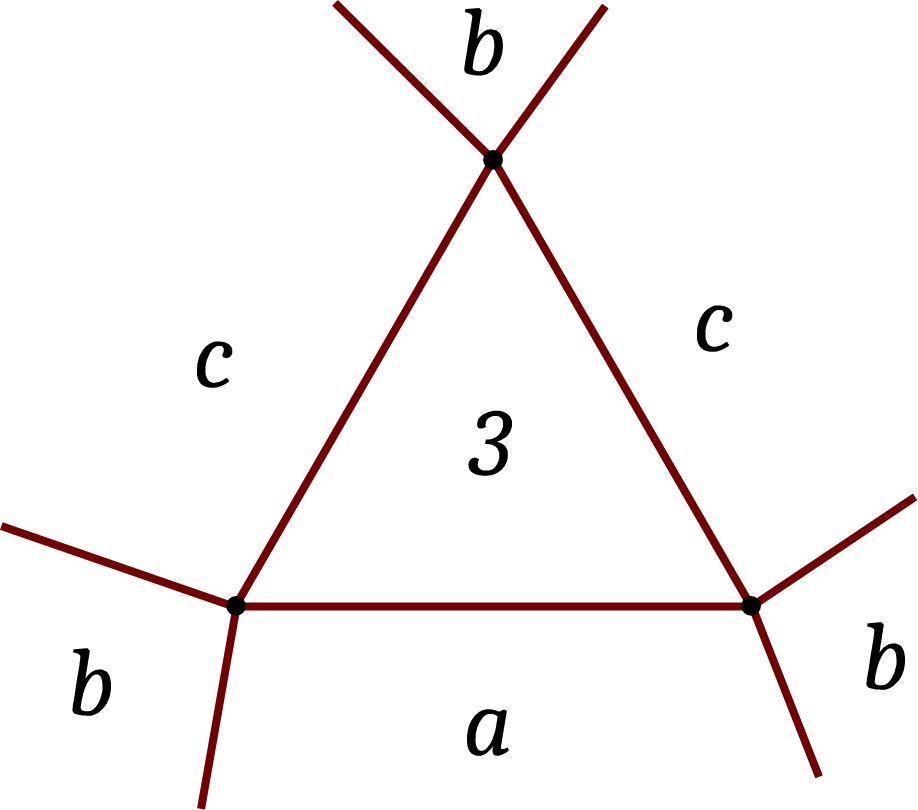
Si a ≥ 4 et b＝3, alors on est dans le cas représenté à gauche ci-dessous, et a＝c. On obtient deux polyèdres, le cuboctaèdre (3,4,3,4) et l'icosidodécaèdre (3,5,3,5). Enfin, si a, b et c sont supérieurs ou égaux à 4, alors a＝c, comme on peut le voir à droite ci-dessous. On obtient le rhombicuboctaèdre (3,4,4,4) et le rhombicosidodécaèdre (3,4,5,4).

Antiprismes (3,3,3, n) où n ≥ 3

Cuboctaèdre (3,4,3,4)

Sur les trois derinières photos, on voit le cube, l'octaèdre, ainsi que les deux ensembles dont l'intersection donne le cuboctaèdre.

Icosidodécaèdre (3,5,3,5)

Sur les deux dernières photos, on peut voir l'icosaèdre complété, ainsi que le dodécaèdre complété.

Rhombicuboctaèdre (3,4,4,4)

C'est presque une troncature du cuboctaèdre, comme on peut le voir sur les trois dernières photos.

Rhombicosidodécaèdre (3,4,5,4)

Là encore, on retrouve le même phénomène qu'avec le polyèdre précédent.

---

page précédente

🏡 polyèdres aimantés

page suivante