Approche informatique
de l'analyse stemmatique
[La première version de cette page a été mise en ligne en 2006. Pour une approche plus poussée des algorithmes permettant d'aider le philologue dans la construction d'un stemma, on pourra se reporter aux travaux du groupe Studia stemmatologica (voir en particulier la bibliographie proposée), ainsi qu'au chapitre 5 du Handbook of Stemmatology paru en 2020 chez De Gruyter sous la direction de Ph. Roelli.]
La critique textuelle, et en particulier la mise au point d'un stemma des témoins manuscrits d'un texte, repose sur l'évaluation de distances plus ou moins grandes entre ces différents textes manuscrits. Or, dans le cas d'une tradition manuscrite importante (comme celle de Martianus Capella), il est extrêmement difficile de se faire une idée rapide des parentés possibles entre les textes. J'ai donc essayé d'appliquer à ce problème un certain nombre de méthodes informatiques qui, si elles ne permettent pas d'établir un stemma assuré (tâche que seule une approche historique et philologique de la tradition manuscrite peut assurer véritablement), fournissent néanmoins un support utile à ce type de réflexion.
L'idée de recourir à des méthodes informatiques, et plus particulièrement bio-informatiques (utilisées notamment en génétique), pour établir les liens de « parenté » entre différents textes descendant de près ou de loin d'un même modèle a déjà été exploitée et évaluée (voir par exemple l'article de P. V. Baret, C. Macé et P. Robinson intitulé « Testing methods on an artificially created textual tradition », ou encore l'article de P. Canettieri, V. Loreto, M. Rovetta et G. Santini, « Ecdotics and information theory », Rivista di filologia cognitiva, décembre 2005, disponible en ligne sur http://filologiacognitiva.let.uniroma1.it/ecdotica.html. Mon objectif était donc de construire un programme informatique incluant certains de ces algorithmes de biologie, et permettant d'obtenir assez simplement un arbre à partir d'un ensemble de fichiers de collation. Il s'agit d'une approche « artisanale » dont l'objectif est de mettre à disposition un logiciel simple ; certaines méthodes utilisées pourraient certainement être largement améliorées.
Les programmes présentés sur cette page sont tous open-source : ils peuvent être librement utilisés, étudiés, copiés et modifiés. Le projet étant encore à l'état expérimental, toutes les remarques, corrections ou suggestions sont les bienvenues (jean-baptiste.guillaumin AT normalesup.org). Enfin, une interface web permettant de tester ce programme est disponible ici.
Sommaire de la page :
- Établissement d'une distance entre des textes
- Détermination d'un arbre à partir d'une matrice de distances
- Fonctionnement du programme
- Évaluation de la validité du procédé
- Utilisation du programme en ligne
Aller à la page de téléchargement
Établissement d'une distance entre les textes
Plutôt que de raisonner sur un « coefficient de proximité » entre les textes (en calculant par exemple le pourcentage de leçons sur lesquels deux manuscrits concordent), il nous a paru intéressant d'établir une distance entre chaque couple de textes à tester, de façon à pouvoir construire et exploiter une matrice des distances sur l'ensemble des textes.
En pratique, il s'agit de collationner, pour un même passage du texte dont on étudie la tradition, le plus grand nombre possible de témoins manuscrits: on place ainsi chaque texte collationné dans un simple fichier texte. On peut ensuite travailler sur l'ensemble de ces fichiers textes pour mettre au point la matrice des distances.
Pour évaluer la distance entre deux fichiers textes, nous utilisons la distance de Levenshtein, qui calcule le nombre minimal de suppressions, d'additions ou de substitutions nécessaires pour passer d'une chaîne de caractères à une autre (on peut bien évidemment ne tenir compte que de certains caractères, c'est-à-dire exclure du calcul toute ponctuation ou plus généralement tout caractère qui n'est pas une lettre de l'alphabet). Ainsi, si l'on considère le premier vers du poème final du De Nuptiis Philologiae et Mercurii de Martianus Capella, et si on appelle R le manuscrit contenant le texte « Habes sanile Marciane fabulam » et E le manuscrit contenant « Habes senilem Martiane fabulam », la distance de Levenshtein entre ces deux textes E et R vaut 3 (substitution de e à a et addition de m pour passer de sanile à senilem, substitution de t à c pour passer de Marciane à Martiane).
Voici le détail de l'algorithme de Levenshtein, que nous nous proposons d'utiliser pour établir la distance:
entier DistanceDeLevenshtein(caractere chaine1[1..longueurChaine1],
caractere chaine2[1..longueurChaine2])
// d est un tableau de longueurChaine1+1 rangées
// et longueurChaine2+1 colonnes
declarer entier d[0..longueurChaine1, 0..longueurChaine2]
// i et j itèrent sur chaine1 et chaine2
declarer entier i, j, coût
pour i de 0 à longueurChaine1
d[i, 0] := i
pour j de 0 à longueurChaine2
d[0, j] := j
pour i de 1 à longueurChaine1
pour j de 1 à longueurChaine2
si chaine1[i] = chaine2[j] alors coût := 0
sinon coût := 1 //on pourra affiner ce coût
//en distinguant différents cas
d[i, j] := minimum(
d[i-1, j ] + 1, // effacement
d[i , j-1] + 1, // insertion
d[i-1, j-1] + coût // substitution
)
retourner d[longueurChaine1, longueurChaine2]
Ainsi, par exemple, lorsque l'on teste la distance entre la chaîne
sanile et la chaîne senilem, les calculs sont les
suivants:
- On définit pour
commencer les valeurs
longueurChaine1=6,
longueurChaine2=7,
chaine1[1..6] (s,a,n,i,l,e)
et chaine2[1..7] (s,e,n,i,l,e,m).
- Ce qui permet d'effectuer les deux premières
boucles de l'algorithme,
et d'obtenir ainsi les premières valeurs de la matrice de dimension 7× 8
(longueurChaine1+1× longueurChaine2+1):
S A N I L E 0 1 2 3 4 5 6 S 1 E 2 N 3 I 4 L 5 E 6 M 7
- On « remplit » ensuite la matrice en
suivant la troisième boucle
présentée plus haut; par exemple, pour remplir la première colonne (« pour
i=1 »), on teste toutes les valeurs de j (de 1 à 7):
-
pour j=1, on a chaine1[1]=S et
chaine2[1]=S donc cout=0
⎧
⎨
⎩d[i−1,j]+1=d[0,1]+1=1+1=2 d[i,j−1]+1=d[1,0]+1=1+1=2 d[i−1,j−1]+cout=d[0,0]+cout=0+0=0
d'où d[1,1]=min(d[i−1,j]+1;d[i,j−1]+1;d[i−1,j−1]+cout)= min(2;2;0)=0
- pour j=2, on a chaine1[1]=S et
chaine2[2]=E donc cout=1
⎧
⎨
⎩d[i−1,j]+1=d[0,2]+1=2+1=3 d[i,j−1]+1=d[1,1]+1=0+1=1 d[i−1,j−1]+cout=d[0,1]+cout=1+1=2
d'où d[1,1]=min(d[i−1,j]+1;d[i,j−1]+1;d[i−1,j−1]+cout)= min(3;1;2)=1
- pour j=3, on a chaine1[1]=S et
chaine2[3]=N donc cout=1
⎧
⎨
⎩d[i−1,j]+1=d[0,3]+1=3+1=4 d[i,j−1]+1=d[1,2]+1=1+1=2 d[i−1,j−1]+cout=d[0,2]+cout=2+1=3
d'où d[1,1]=min(d[i−1,j]+1;d[i,j−1]+1;d[i−1,j−1]+cout)= min(4;2;3)=2
- etc., jusqu'à j+7, ce qui permet d'obtenir,
pour i=1, la colonne
suivante:
S A N I L E 0 1 2 3 4 5 6 S 1 0 E 2 1 N 3 2 I 4 3 L 5 4 E 6 5 M 7 6
-
pour j=1, on a chaine1[1]=S et
chaine2[1]=S donc cout=0
- Pour i=2, on teste à nouveau toutes les
valeurs de j; ce qui
donne:
- pour j=1, on a
chaine1[2]=E et chaine2[1]=S, donc
cout=1
⎧
⎨
⎩d[i−1,j]+1=d[1,1]+1=0+1=1 d[i,j−1]+1=d[2,0]+1=2+1=3 d[i−1,j−1]+cout=d[1,0]+cout=1+1=2
d'où d[2,1]=min(d[i−1,j]+1;d[i,j−1]+1;d[i−1,j−1]+cout)= min(1;3;2)=1
- pour j=2, on a chaine1[2]=E et
chaine2[2]=A, donc cout=1
⎧
⎨
⎩d[i−1,j]+1=d[1,2]+1=1+1=2 d[i,j−1]+1=d[2,1]+1=1+1=2 d[i−1,j−1]+cout=d[1,1]+cout=0+1=1
d'où d[2,2]=min(d[i−1,j]+1;d[i,j−1]+1;d[i−1,j−1]+cout)= min(2;2;1)=1
- Et ainsi de suite, jusqu'à j=7, ce qui donne
la deuxième colonne:
S A N I L E 0 1 2 3 4 5 6 S 1 0 1 E 2 1 1 N 3 2 2 I 4 3 3 L 5 4 4 E 6 5 5 M 7 6 6
- pour j=1, on a
chaine1[2]=E et chaine2[1]=S, donc
cout=1
- Et ainsi de suite, jusqu'à i=6. A la fin
des itérations, on obtient
la matrice suivante:
S A N I L E 0 1 2 3 4 5 6 S 1 0 1 2 3 4 5 E 2 1 1 2 3 4 4 N 3 2 2 1 2 3 4 I 4 3 3 2 1 2 3 L 5 4 4 3 2 1 2 E 6 5 5 4 3 2 1 M 7 6 6 5 4 3 2La distance de Levenshtein entre les deux chaînes testées correspond à d[longueurChaine1,longueurChaine2], c'est-à-dire au nombre « en bas, à droite », qui ici vaut 2.
On a donc l'algorithme suivant:
entier DistanceDeLevenshtein(tableau texte1[1..longueurTexte1],
tableau texte2[1..longueurTexte2])
// d est un tableau de longueurTexte1+1 rangées
// (et longueurTexte1 correspond au nombre d'éléments dans le tableau
// que constitue le texte)
// et longueurTexte2+1 colonnes
declarer entier d[0..longueurTexte1, 0..longueurTexte2]
// i et j itèrent sur texte1 et texte2
declarer entier i, j, coût, poids
poser d[0, 0] = 0
pour i de 1 à longueurTexte1
d[i, 0] := d[i-1, 0] + poids(Texte1[i])
pour j de 1 à longueurTexte2
d[0, j] := d[j-1, 0] + poids(Texte2[j])
pour i de 1 à longueurTexte1
pour j de 1 à longueurTexte2
coût := DistanceDeLevenshtein(texte1[i], texte2[j])
d[i, j] := minimum(
d[i-1, j ] + poids(Texte1[i]),
d[i , j-1] + poids(Texte2[j]),
d[i-1, j-1] + coût
)
retourner d[longueurTexte1, longueurTexte2]
Par exemple, pour texte1 = {habes;senilem;martiane} et texte2
=
{habes;sanile;marciane}, on a:| ⎧ ⎪ ⎪ ⎨ ⎪ ⎪ ⎩ |
|
On construit ainsi la matrice suivante:
habes senilem martiane
0 5 12 20
habes 5
sanile 11
marciane 19
On réalise ensuite les itérations, en commençant par calculer
d[1,1]=min(d[0,1]+poids(texte1[1]);
d[1,0]+poids(texte2[1]);
d[0,0]+coût):| ⎧ ⎨ ⎩ |
|
D'où d[1,1]=0
Puis d[1,2]=min(d[0,2]+poids(texte1[1]); d[1,1]+poids(texte2[2]); d[0,1]+coût):
| ⎧ ⎨ ⎩ |
|
D'où d[1,2]=6
Après avoir réalisé toutes les itérations, on obtient la matrice:
habes senilem martiane
0 5 12 20
habes 5 0 7 15
sanile 11 6 2 10
marciane 19 14 10 3
Ce résultat se vérifie très facilement empiriquement (on a besoin de trois
modifications
pour passer du premier texte au second); l'intérêt de cette méthode
est de pouvoir travailler sur des textes de plusieurs centaines de mots en
un temps raisonnable.Le programme distances.ml (écrit en objective caml, voir la version 1, la version 2.1, la version 2.2, ou la version 3.1) permet de faire ce type de calcul sur les fichiers de collation. La distance ne tient compte ni de la ponctuation, ni des espaces blancs, ni des passages à la ligne, ni, plus généralement, de tous les signes qui ne sont pas des caractères de l'alphabet, sauf de l'astérisque qui sert à représenter les lettres effacées ou illisibles (la distance de * à n'importe quelle lettre valant alors la moitié d'une distance entre deux lettres différentes, de manière à en tenir compte sans lui donner une influence trop importante). Par ailleurs, on pose que la distance d'une majuscule à une minuscule, d'un u à un v ou encore d'un i à un j vaut 0 (ces lettres n'étant pas distinctes en latin). Enfin, la version 2.2 du programme travaille sur des « coûts » de substitution différents en fonction des lettres comparées (ainsi le « coût » du passage de m à n est moindre que celui du passage de m à r par exemple). Dans la version 2.2, on peut également transcrire par « - » l'abréviation marquant une nasale. Ainsi u- sera compté comme très proche de un et de um. La distance de e à æ (en un seul caractère) vaut la moitié d'une distance normale. D'une manière générale, ces raffinements de détail n'influent guère sur le calcul d'ensemble.
Une fois le calcul fait pour chaque paire de textes, on obtient un tableau de la forme suivante (les valeurs numériques qui suivent ont été obtenues à partir du texte du poème qui ouvre le livre IX de Martianus) :
A B C D E G H K M P R T W
A 0.0 47.0 59.5 42.5 49.0 58.0 60.5 70.0 50.0 51.0 47.0 58.5 52.0
B 47.0 0.0 40.0 15.5 31.0 44.0 53.5 59.0 34.0 31.0 35.0 43.0 43.0
C 59.5 40.0 0.0 37.5 26.5 44.5 69.5 59.5 41.5 33.5 56.5 49.0 60.5
D 42.5 15.5 37.5 0.0 25.5 36.5 46.0 51.5 26.5 25.5 33.5 36.5 39.5
E 49.0 31.0 26.5 25.5 0.0 35.0 58.0 50.0 27.0 26.0 44.0 35.0 41.0
G 58.0 44.0 44.5 36.5 35.0 0.0 71.0 56.0 34.0 39.0 57.0 44.5 55.0
H 60.5 53.5 69.5 46.0 58.0 71.0 0.0 84.5 57.0 55.0 51.5 70.0 61.5
K 70.0 59.0 59.5 51.5 50.0 56.0 84.5 0.0 42.0 51.0 74.0 60.0 71.0
M 50.0 34.0 41.5 26.5 27.0 34.0 57.0 42.0 0.0 25.0 47.0 36.0 50.0
P 51.0 31.0 33.5 25.5 26.0 39.0 55.0 51.0 25.0 0.0 46.0 41.0 45.0
R 47.0 35.0 56.5 33.5 44.0 57.0 51.5 74.0 47.0 46.0 0.0 59.0 50.0
T 58.5 43.0 49.0 36.5 35.0 44.5 70.0 60.0 36.0 41.0 59.0 0.0 56.5
W 52.0 43.0 60.5 39.5 41.0 55.0 61.5 71.0 50.0 45.0 50.0 56.5 0.0
Détermination d'un arbre à partir de la matrice
Des algorithmes utilisés en biologie pour établir des arbres phylogénétiques peuvent alors être appliqués à cette matrice, afin de faire émerger un arbre (non enraciné) matérialisant les rapprochements possibles entre ces textes, à partir des distances fournies. Il convient cependant de rester prudent face au résultat obtenu, qui bien entendu ne peut pas tenir compte d'une éventuelle contamination entre les textes, et qui ne prend pas en compte la dimension temporelle de la transmission. L'arbre obtenu constitue ainsi une modélisation des distances mathématiques entre les textes, et ne saurait donc en aucun cas être considéré comme un stemma à part entière; il peut toutefois être utile pour montrer l'« agglomération » de certains textes que l'on peut alors considérer comme proches.
L’algorithme neighbor-joining
L’objectif général de cet algorithme est de construire un arbre phylogénétique à partir d’une matrice des distances, tout en conservant la représentation des distances dans l’arbre obtenu.
Vocabulaire
On appelle OTU (Operational Taxonomic Unit) une « feuille » de l’arbre (c’est-à-dire, en phylogénie, une espèce, et dans notre cas un texte). La matrice des distances est donc établie sur l’ensemble des paires d’OTU.
Une paire de « voisins » (neighbors) est une paire d’OTU connectés par un seul nœud intermédiaire dans un arbre non enraciné. Par exemple, les OTU 1 et 2 de l’exemple suivant sont voisins (ils sont connectés par l’intermédiaire d’un seul nœud, A), de même que 5 et 6 (par E) ou encore 7 et 8 (par F):
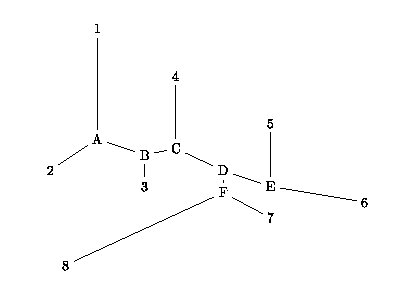
Fig. 1
Si, dans cette même figure, on combine les OTU 1 et 2, alors les OTU (1-2)=A
et 3 sont voisins. De même, l’OTU ((1–2)–3)=B
sera voisin de 4. Il est donc possible de définir la topologie de l’arbre
en regroupant les OTU par paires successives de « voisins ».
Principes généraux de l’algorithme
On appelle Dij la distance entre les OTU i et j, Lab la longueur de la branche reliant les nœuds a et b, et N le nombre général d’OTU.
Si on considère un arbre en étoile (dans lequel tous les OTU sont équidistants), on peut calculer la somme des longueurs des branches (S0) grâce à la formule suivante:
| S0 = |
| LiX = |
|
| Dij |
(on divise par N−1 car chaque branche est comptée N−1 fois dans la somme.)
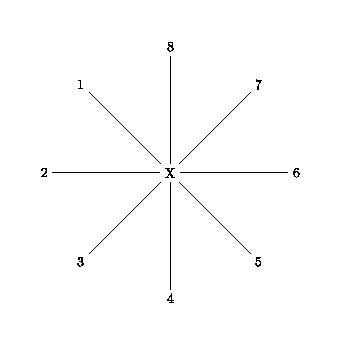
Fig. 2
Si l’on regroupe deux OTU « voisins » (par exemple 1 et 2), on obtient alors une figure de ce type:
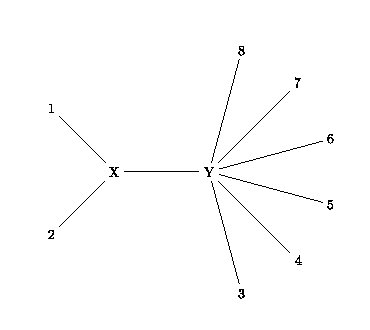
Fig. 3
On peut alors calculer la longueur de la branche entre X et Y (LXY) de la manière suivante:
| LXY = |
| [ |
| (D1k+D2k)−(N−2)(L1X+L2X)−2 |
| LiY] |
En effet, ∑k=3N(D1k+D2k) correspond à la
somme de toutes les distances qui incluent LXY: on soustrait à cette
somme toutes les branches comptées « en trop ».
On a alors les égalités suivantes:
| ⎧ ⎪ ⎪ ⎨ ⎪ ⎪ ⎩ |
|
La somme de toutes les longueurs des branches de cette figure (S12) est alors obtenue de la manière suivante:
| S12=LXY+(L1X+L2X)+ |
|
En remplaçant ces diverses expressions par les égalités obtenues précédemment, on obtient finalement
(sans lien avec X ni avec Y):
| S12 = |
|
| + |
| D12+ |
|
|
On a ici choisi arbitrairement de regrouper 1 et 2. Mais en général,
face à la matrice des distances, on ne sait pas a priori quels sont les
« voisins ». Le principe de l’algorithme « neighbor-joining » est donc de
calculer, dans une matrice des distances donnée, tous les Sij, afin de
choisir le plus petit (c’est-à-dire la paire de distances qui minimise la
longueur globale des branches de l’arbre).
Après avoir trouvé ces deux OTU voisins qui minimisent la longueur totale
des branches de l’arbre, on leur substitue un seul OTU, qui représente le
nœud entre ces deux OTU. On recalcule alors toutes les distances entre
ce nœud et les OTU restants. Dans notre
exemple, on aura ainsi l’OTU (1−2), dont on peut calculer la distance par
rapport à tous les autres OTU de la façon suivante:
| D(1−2)j= |
| (3≤ j < N) |
Ces N−1 distances définissent une nouvelle matrice à laquelle on
applique le même algorithme.
On calcule par ailleurs la distance des OTU 1 et 2 à ce nœud X
selon la formule de Fitch et Margoliash:
| ⎧ ⎪ ⎪ ⎪ ⎨ ⎪ ⎪ ⎪ ⎩ |
|
avec D1Z=1/N−2∑i=3ND1i et D2Z=1/N−2∑i=3ND2i (Z représentant donc le groupe de tous les OTU du début sauf 1 et 2).
Si, dans une itération ultérieure de l’algorithme, l’un des éléments qui
minimisent la longueur totale est lui-même un nœud, on soustrait à la distance ainsi obtenue la moitié de la
distance entre les OTU connectés par l’intermédiaire de ce nœud: dans notre exemple, si le
nœud 1−2 est choisi dans une itération de l’algorithme, on soustraira
D12/2 à la distance obtenue selon la formule ci-dessus. En
d’autres termes, sur la figure ci-dessus (fig. 3), LAB=L(1−2)B−D12/2.
Pour résumer, l’algorithme « neighbor-joining » répète, pour N
décroissant de la dimension initiale de la matrice à 3, les étapes suivantes:
-
Choix de la paire de distances (i,j) qui minimise
Sij= 1 2(N−2) N ∑ k≠ i, k≠ j (Dik+Djk) + 1 2 Dij+ 1 N−2 ∑ a,b≠ i, a,b≠ j Dab - Calcul d’une nouvelle matrice de dimension N−1 en considérant (i,j) comme un seul OTU.
- Calcul de la distance de i et de j à leur nœud commun.
Exemple concret
Soit la matrice suivante (qui équivaut aux distances — arrondies pour simplifier — entre les 5 premiers manuscrits de notre exemple, donc N=5):
A B C D E
A 0 47 59 42 49
B 47 0 40 15 31
C 59 40 0 37 26
D 42 15 37 0 25
E 49 31 26 25 0
L’algorithme calcule tout d’abord la somme totale des longueurs des branches pour
chaque paire d’OTU, selon la formule explicitée plus haut:
| ⎧ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎨ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎩ |
|
D’où, avec les valeurs numériques:
| ⎧ ⎪ ⎪ ⎪ ⎪ ⎪ ⎨ ⎪ ⎪ ⎪ ⎪ ⎪ ⎩ |
|
C’est donc la paire (C,E) qui minimise la longueur totale de l’arbre. On
appelle (CE) le nœud entre C et E, et on calcule les longueurs
C(CE) et E(CE):
| ⎧ ⎪ ⎪ ⎪ ⎨ ⎪ ⎪ ⎪ ⎩ |
|
Soit, avec les valeurs chiffrées:
| ⎧ ⎨ ⎩ |
|
C est donc à une distance de 18.17 du nœud, et E à une distance
de 7.83. On peut noter cela de la façon suivante: (C:18.166,E:7.833), ce
qui permet de décrire mathématiquement le nœud (CE).
On calcule alors la distance de (CE) à chacun des OTU restants:
| ⎧ ⎪ ⎪ ⎪ ⎪ ⎪ ⎨ ⎪ ⎪ ⎪ ⎪ ⎪ ⎩ |
|
Ce qui donne la nouvelle matrice:
A B (CE) D A 0.0 47.0 54.0 42.0 B 47.0 0.0 35.5 15.0 (CE) 54.0 35.5 0.0 31.0 D 42.0 15.0 31.0 0.0
On reprend alors l’algorithme au début, avec N=4. Ainsi, on calcule:
| ⎧ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎨ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎩ |
|
On trouve donc deux paires qui minimisent la longueur totale: (A,(CE)) et
(B,D). Si l’on choisit comme voisins A et (CE), on appelle (ACE) le
nœud entre A et (CE), et on calcule les longueurs A(ACE) et (CE)(ACE):
| ⎧ ⎪ ⎪ ⎪ ⎨ ⎪ ⎪ ⎪ ⎩ |
|
Dans la seconde de ces distances, on soustrait la moitié de la distance de
C à E car (CE) est déjà un nœud formé de deux OTU.
On a ainsi: (A:32.625,(C:18.166,E:7.833)).
On calcule à nouveau la distance de (ACE) à chacun des OTU restants:
| ⎧ ⎪ ⎪ ⎪ ⎨ ⎪ ⎪ ⎪ ⎩ |
|
Ce qui donne la nouvelle matrice (avec N=3, donc on arrêtera l’algorithme à la fin de cette itération):
(ACE) B D
(ACE) 0.0 41.25 36.5
B 41.25 0.0 15.0
D 36.5 15.0 0.0
Alors S(ACE)B=S(ACE)D=SBD = 46.375. On choisit (arbitrairement
puisque les trois longueurs sont égales) la paire (ACE)B et on appelle le
nœud (ACEB). Alors:
| ⎧ ⎪ ⎪ ⎪ ⎨ ⎪ ⎪ ⎪ ⎩ |
|
Ce qui donne les « coordonnées »: ((A:32.625,(C:18.166,E:7.833)):4.375,B:9.875).
Il nous reste alors la longueur de la branche reliant (ACEB) à D:
D(ACE)D+DBD/2=36.5+15/2=25.75. On en déduit la
distance de (ACEB) à D:
D(ACEB)D−D(ACE)B/2=5.125.
On obtient ainsi la description mathématique de l’ensemble de l’arbre:
((A:32.625,(C:18.166,E:7.833):8.375):4.375,B:9.875,D:5.125), ce qui
correspond au résultat graphique suivant:
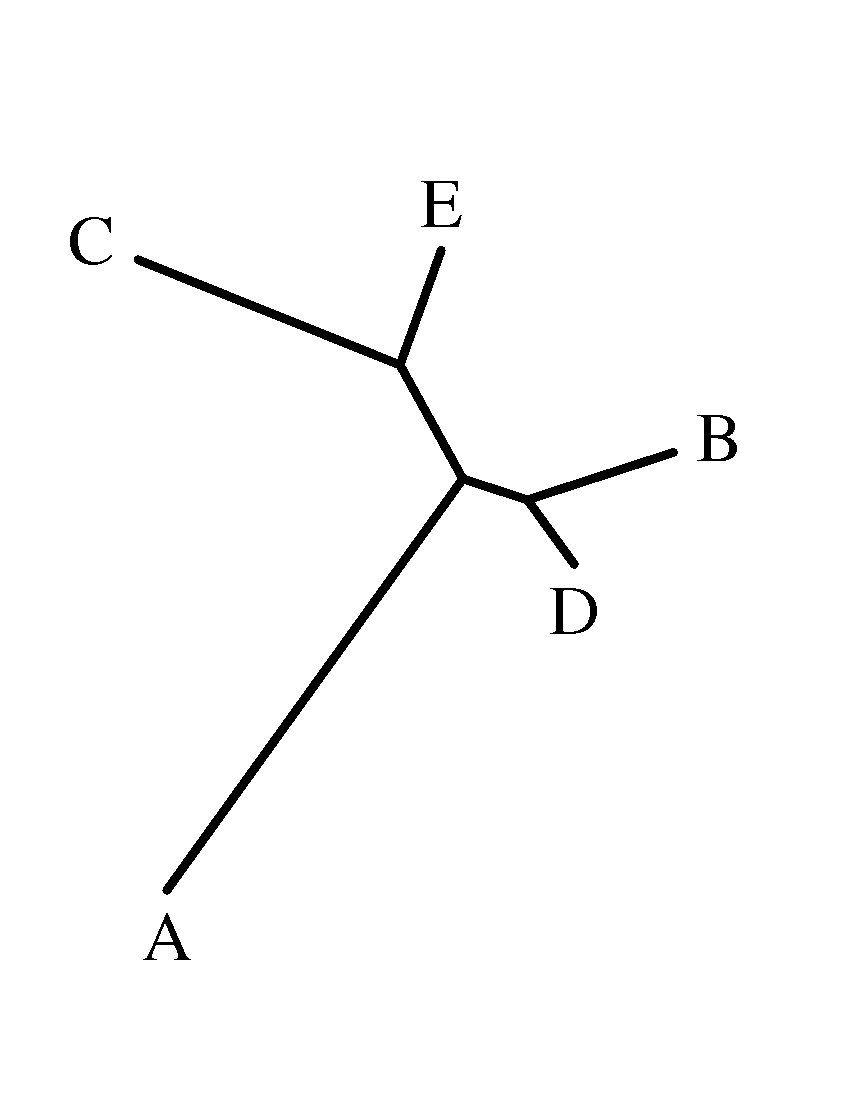
L’intérêt de l’algorithme est donc non seulement de proposer
les embranchements la plus probables, mais également de conserver au maximum les
distances de la matrice (il est en général impossible — sauf cas
particulier peu probable — de les conserver
parfaitement puisqu’on se situe au départ dans un espace métrique à N
dimensions). En effet, si l’on reconstitue les distances à partir de
l’arbre obtenu, on arrive à un résultat très proche de la matrice
de départ:
- DAB=32.625+4.375+9.875=46.875 (47 dans la matrice)
- DAC=32.625+8.375+18.166=59.166 (59 dans la matrice)
- DAD=32.625+4.375+5.125=42.125 (42 dans la matrice)
- DAE=32.625+8.325+7.833=48.784 (49 dans la matrice)
- DBC=9.875+4.375+8.375+18.166=40.791 (40 dans la matrice)
- DBD=9.875+5.125=15 (15 dans la matrice)
- DBE=9.875+4.375+8.375+7.833=30.458 (31 dans la matrice)
- DCD=18.166+8.375+4.375+5.125=36.041 (36 dans la matrice)
- DCE=18.166+7.833=26 (26 dans la matrice)
- DDE=5.125+4.375+8.375+7.833=25.708 (25 dans la matrice)
Implémentation de l'algorithme neighbor-joining
Dans la dernière version du paquet calculs_philologiques, l'algorithme neighbor-joining est implémenté dans le programme distances.ml : ainsi, le même programme calcule les distances et les interprète. Le programme distances.ml affiche en sortie la représentation de l'arbre dans un format « LISP-like », avec les nœuds parenthésés et les distances qui correspondent. En copiant ce résultat dans un fichier intree, on peut lancer le programme drawtree du package phylip, qui permet d'obtenir un arbre au format ps. Toutes ces opérations sont réalisées automatiquement par le script calcul du paquet calculs_philologiques.
Utilisation du programme neighbor (version 1 du package calculs_philologiques seulement)
Le programme neighbor du package Phylip permet de lancer cet algorithme sur un fichier infile contenant la matrice, ainsi que l'indication du nombre de manuscrits (ici 18) sur la première ligne: ce fichier est automatiquement généré par distances.ml.
Le programme neighbor génère deux fichiers:
- outtree, qui contient la description mathématique de l'arbre.
- outfile, qui donne une représentation graphique sommaire de l'arbre et précise les distances entre les différents nœuds.
Représentation graphique
Le programme drawtree utilise le fichier intree (représentation « LISP-like » de l'arbre) pour générer une image de l'arbre au format postscript (convertie ci-dessous en jpg), en prenant en compte les distances entre les différents textes:
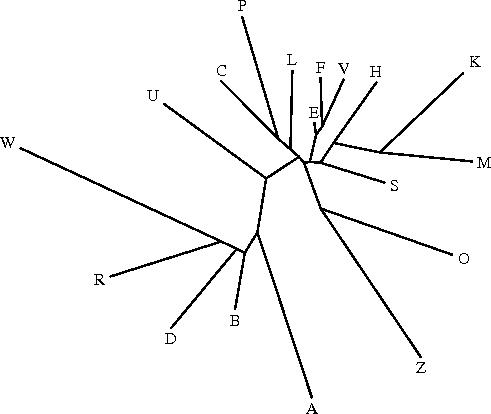
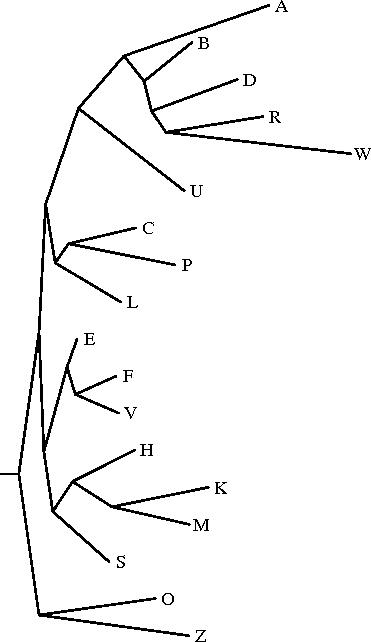
Le programme drawgram permet d'obtenir un dendrogramme (enraciné) à partir du même fichier intree; mais seul le philologue peut décider de l'endroit où il convient de placer l'archétype (c'est-à-dire la racine du dendrogramme): il faut donc toujours vérifier que la représentation fournie par drawtree est valide d'un point de vue philologique. Ce programme permet d'obtenir différents styles de dendrogrammes, en particulier (cf. ci-dessous) des phénogrammes (exemple n°1), des curvogrammes (exemple n°2), ou encore des arbres circulaires (exemple n°3).
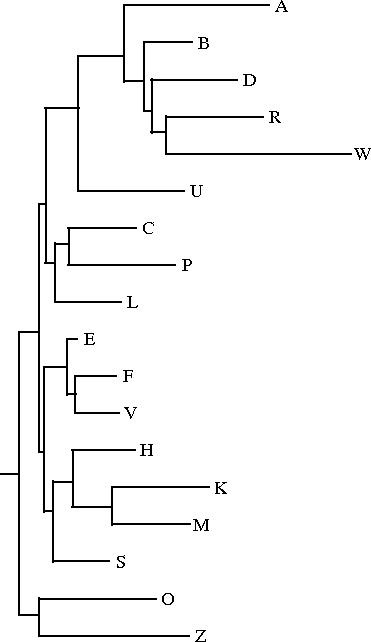 | 
|
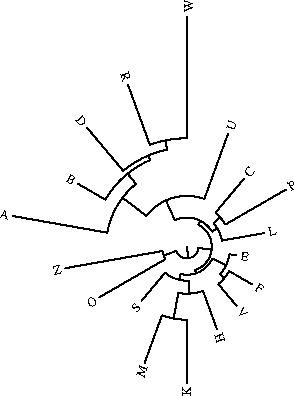
Fonctionnement du programme
Le programme permettant d'obtenir un arbre au format ps à partir d'un répertoire de fichiers de collation fonctionne sur les systèmes Unix (y compris Mac OSX en ligne de commande): l'interface entre les différents programmes utilise des commandes shell unix, le programme calculant les distances est écrit en ocaml (assurez-vous d'avoir un compilateur ocaml installé), et les programmes du package phylip sont écrits en C.
Voici la liste des fichiers contenus dans le paquet calculs_philologiques_3.1 (dernière version) :
- distances.ml: calcule la distance de Levenshtein entre les différents fichiers textes fournis et applique l'algorithme neighbor-joining sur cette matrice.
- install.sh (shell UNIX): compile les utilitaires; rien n'est installé en dehors du répertoire.
- calcul: utilitaire (en shell) qui constitue l'interface entre les différents programmes. La commande ./calcul REPERTOIRE/ lance le calcul des distances et la génération d'un arbre à partir des fichiers de collation contenus dans le répertoire REPERTOIRE/ . GNU-GPL.
- utilitaires.tar.gz: contient les utilitaires des packages phylip utiles pour notre programme (l'archive est décompactée, et les programmes sont compilés automatiquement par install.sh).
Voici la liste des fichiers contenus dans le paquet calculs_philologiques_2.2 :
- distances.ml: calcule la distance de Levenshtein entre les différents fichiers textes fournis et applique l'algorithme neighbor-joining sur cette matrice.
- install.sh (shell UNIX): compile les utilitaires; rien n'est installé en dehors du répertoire.
- calcul: utilitaire (en shell) qui constitue l'interface entre les différents programmes. La commande ./calcul REPERTOIRE/ lance le calcul des distances et la génération d'un arbre à partir des fichiers de collation contenus dans le répertoire REPERTOIRE/ .
- HOWTO: manuel sommaire.
- gpl.txt: licence GNU-GPL.
- utilitaires.tar.gz: contient les utilitaires des packages phylip utiles pour notre programme (l'archive est décompactée, et les programmes sont compilés automatiquement par install.sh).
Voici la liste des fichiers contenus dans le paquet calculs_philologiques_2 :
- distances.ml: calcule la distance de Levenshtein entre les différents fichiers textes fournis et applique l'algorithme neighbor-joining sur cette matrice.
- install.sh (shell UNIX): compile les utilitaires; rien n'est installé en dehors du répertoire.
- calcul: utilitaire (en shell) qui constitue l'interface entre les différents programmes. La commande ./calcul REPERTOIRE/ lance le calcul des distances et la génération d'un arbre à partir des fichiers de collation contenus dans le répertoire REPERTOIRE/ .
- HOWTO: manuel sommaire.
- gpl.txt: licence GNU-GPL.
- utilitaires.tar.gz: contient les utilitaires des packages phylip utiles pour notre programme (l'archive est décompactée, et les programmes sont compilés automatiquement par install.sh).
Voici la liste des fichiers contenus dans le paquet calculs_philologiques (ancienne version) :
- distances.ml: calcule la distance de Levenshtein entre les différents fichiers textes fournis.
- install.sh (écrit en shell): compile les utilitaires; rien n'est installé en dehors du répertoire.
- calcul: utilisaire (en shell) qui constitue l'interface entre les différents programmes. La commande ./calcul REPERTOIRE/ lance le calcul des distances et la génération d'un arbre à partir des fichiers de collation contenus dans le répertoire REPERTOIRE/ .
- HOWTO: manuel sommaire.
- gpl.txt: licence GNU-GPL.
- utilitaires.tar.gz: contient les utilitaires du package phylip utiles pour notre programme (l'archive est décompactée, et les programmes sont compilés automatiquement par install.sh). Les fichiers contenus dans ce répertoire d'utilitaires sont les suivants:
- dist.c
- dist.h
- draw.c
- draw.h
- draw2.c
- drawgram.c
- drawtree.c
- fontfile (fichier de police postscript qui permet à drawtree de construire l'arbre)
- neighbor.c
- phylip.c
- phylip.h
Évaluation de la validité du procédé
Les fichiers d'exemple fournis dans le répertoire EXEMPLE correspondent à la collation du poème final du De Nuptiis Philologiae et Mercurii de Martianus Capella; cependant, pour des raisons liées aux aléas de la transmission du texte, ce poème final ne donne pas une vue très exacte des rapports entre les manuscrits essentiels (certains manuscrits importants ont perdu la fin du texte, qui est parfois rajoutée de seconde main, comme dans le manuscrit H). Nous nous proposons donc de tester la validité philologique du procédé en nous appuyant sur le poème qui ouvre le livre IX du De Nuptiis Philologiae et Mercurii, et qui est présent de première main dans tous les manuscrits les plus importants. Nous disposons par ailleurs d'un stemma des 12 manuscrits les plus importants, élaboré selon des arguments philologiques par Danuta Shanzer (« Felix Capella : minus sensus quam nominis pecudalis », Classical Philology, 1986) :
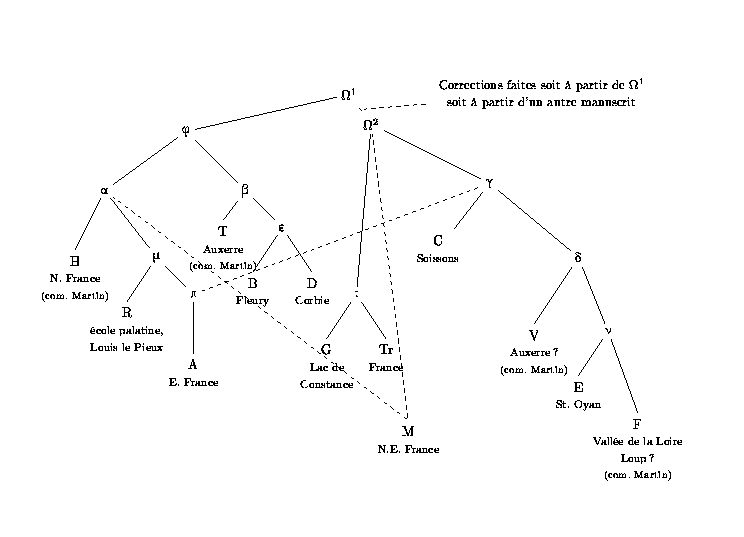
Collationnons alors le texte des mêmes manuscrits :
- A : Londres, Brit. Lib. Harley 2685
- B : Bamberg, class. 39
- C : Paris, B. N. lat. 8669
- D : Paris, B. N. lat. 8670
- E : Besançon, Bibl. mun. 594
- F : Oxford, Bodl. Lib. Laud. lat. 118
- G : Bruxelles, B. R. 9565-9566
- H : Vatican, Reg. lat. 1987
- M : Paris, B. N. lat. 8671
- R : Karlsruhe, Reichenau LXXIII
- T : Vatican, Reg. lat. 1535
- V : Leyde, Voss. lat. F. 48
- (le manuscrit Tr, Trèves, Priest. 100, ne contient pas le livre IX)
Un test automatique sur l'ensemble de ces fichiers de collation, en minimisant les différences orthographiques (pour éviter par exemple que la différence entre les graphies e et ae ne prenne trop d'importance), donne l'arbre suivant :
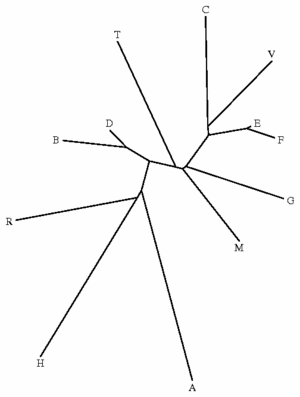
On voit donc que le procédé automatique donne une bonne approximation des relations de proximité, et éventuellement de parenté, entre les manuscrits, puisqu'on retrouve les principaux nœuds du stemma de D. Shanzer. Seul le manuscrit T est un peu décalé par rapport à sa place dans le stemma de D. Shanzer (on l'attendrait plus proche de B et D), mais cela peut être dû à la relative brièveté du passage collationné, qui ne permet pas toujours d'établir des distances vraiment significatives. Par ailleurs, ce procédé ne permet pas de tenir compte d'une éventuelle contamination, que seule une étude philologique plus poussée peut établir.
Utilisation du programme en ligne
Pour avoir une idée du fonctionnement du programme et des résultats obtenus, vous pouvez tester cette interface en ligne, en entrant au moins trois textes différents. Vous pouvez par exemple utiliser les textes donnés ci-dessus en exemple, c'est-à-dire les différentes versions du poème liminaire du livre IX des Noces de Philologie et de Mercure, ou encore les différentes versions du poème final.