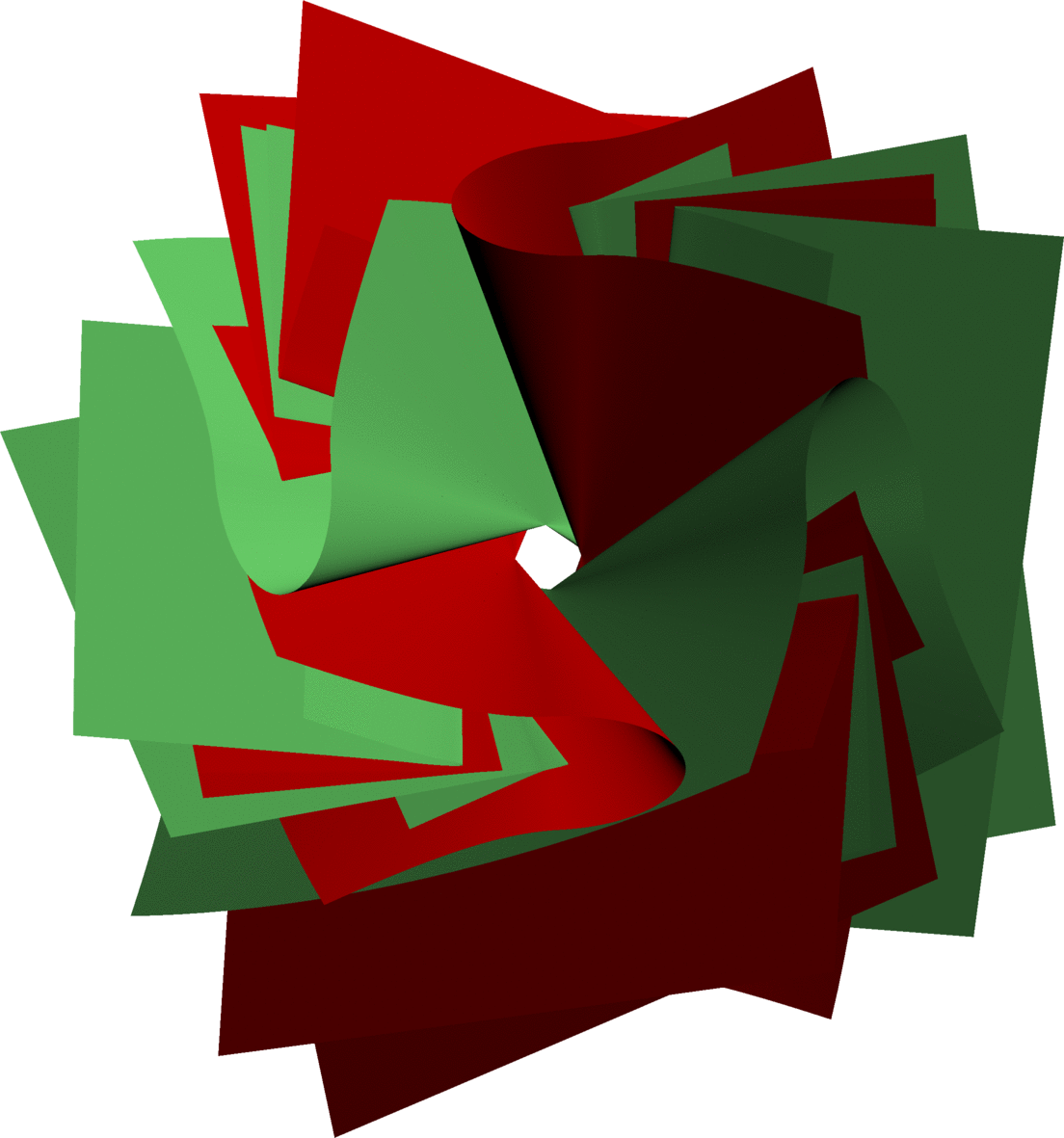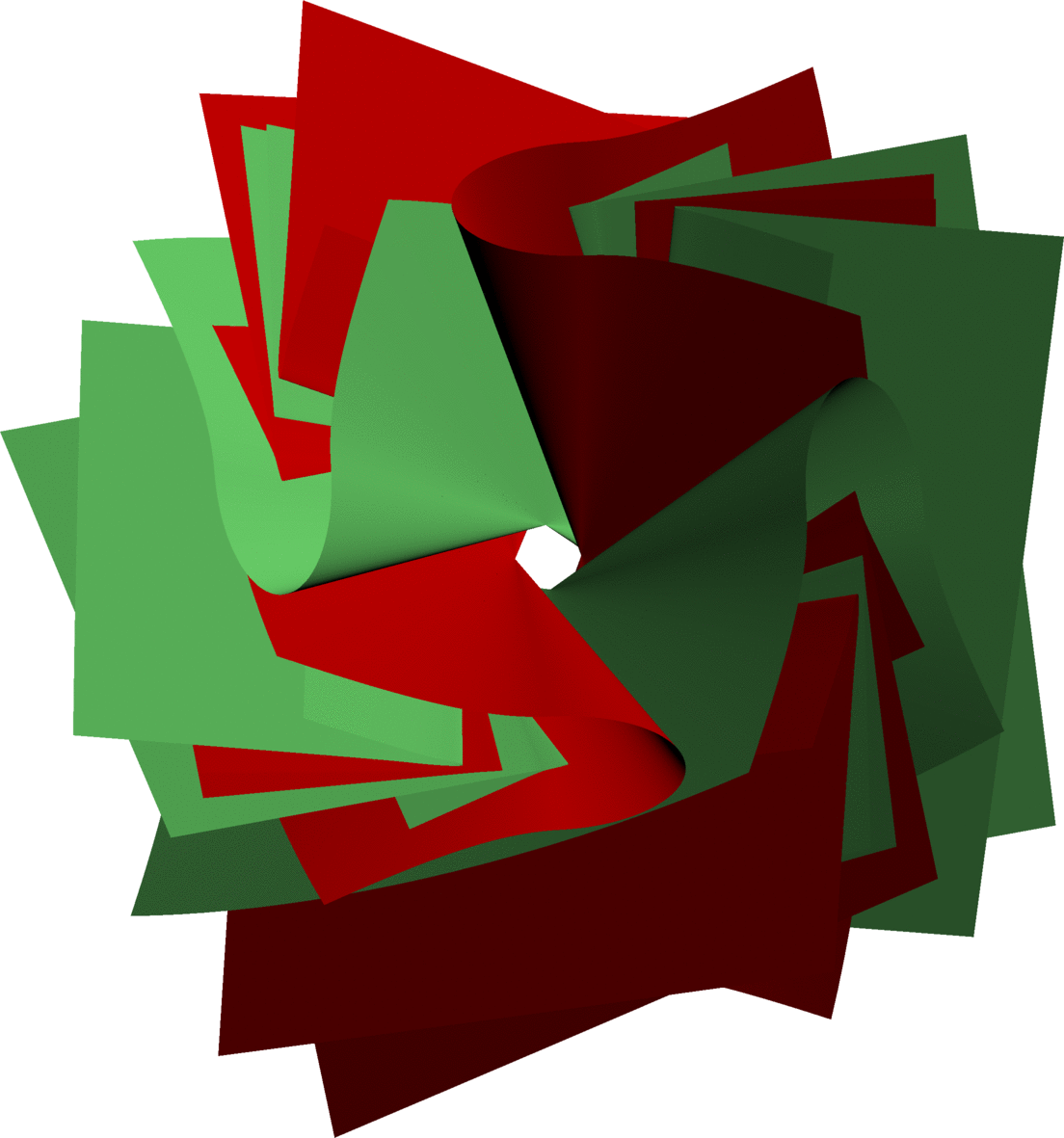Ilia Smilga : Introduction rapide aux groupes libres de transformations affines agissant proprement

Considérons une transformation affine g de R³ définie de la façon suivante :

elle multiplie toutes les longueurs dans la direction z par une certaine constante λ>>1;
elle divise toutes les longueurs dans la direction y par la même constante λ;
et elle translate par une certaine longueur fixée le long de la direction x.

Voici l'action de cette transformation g sur un pavé :

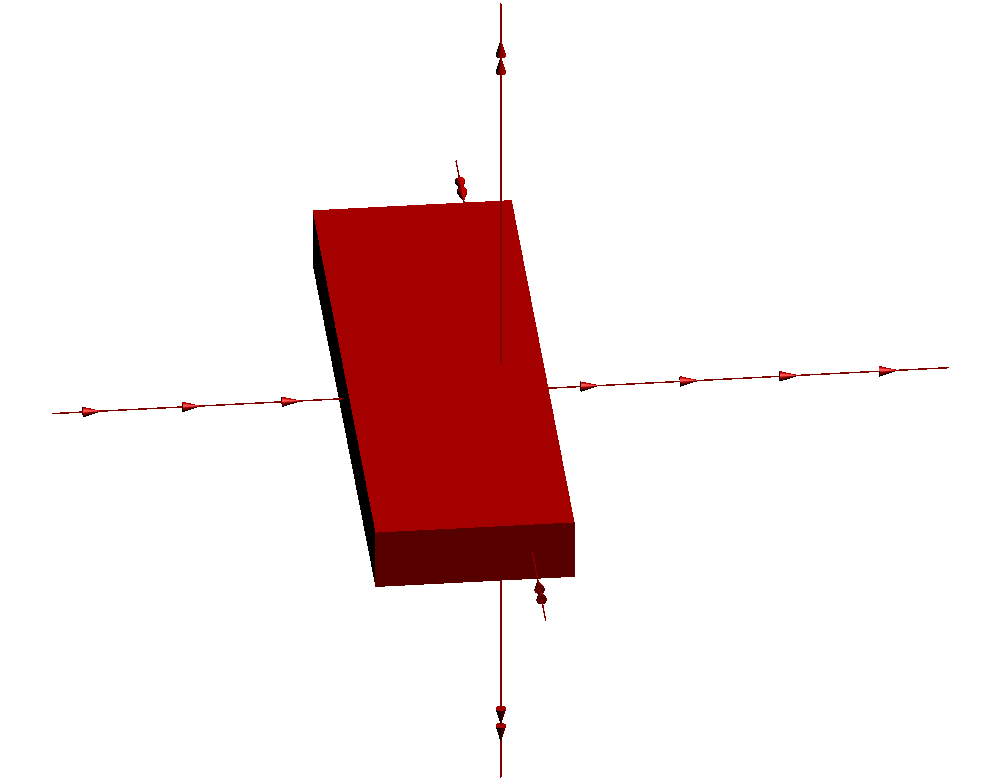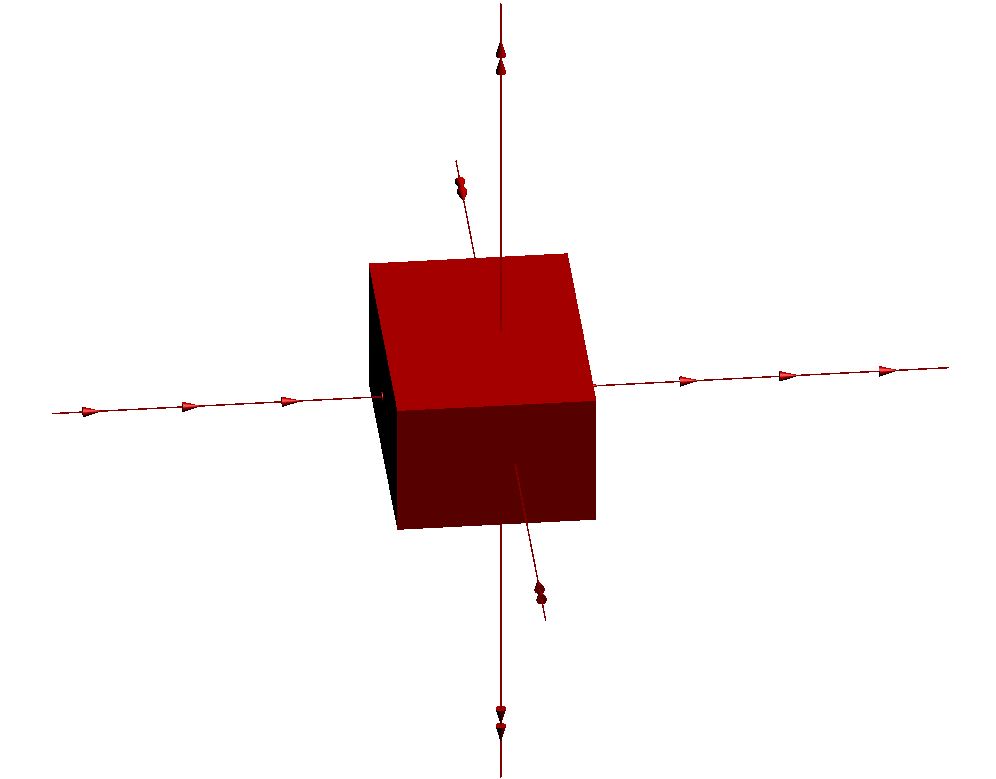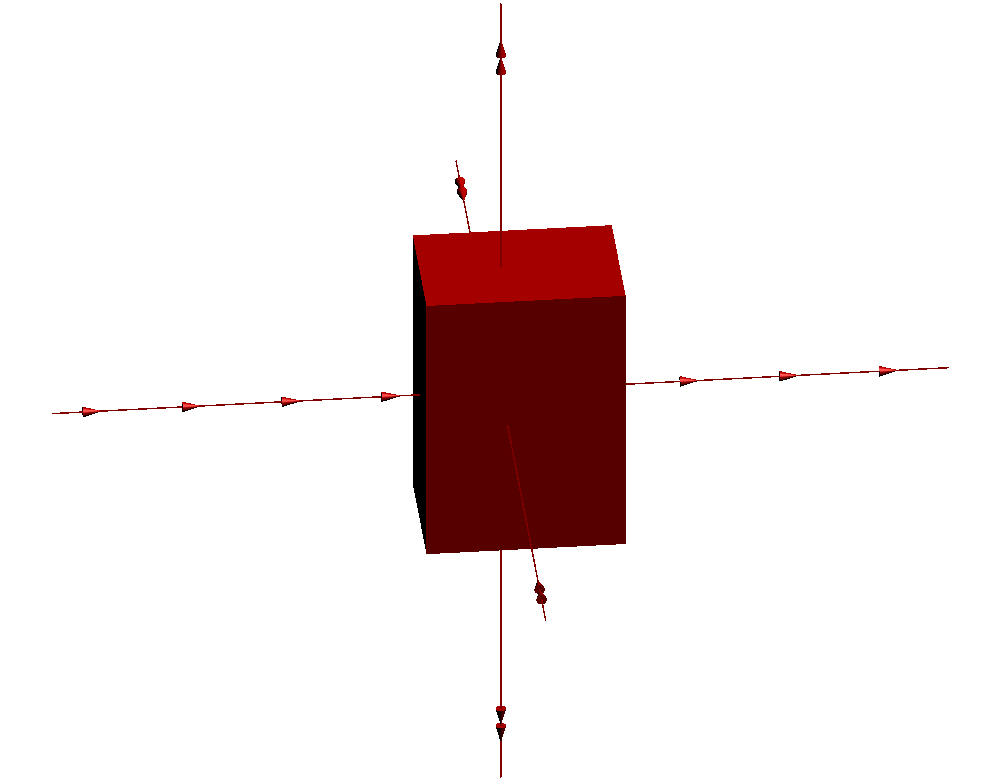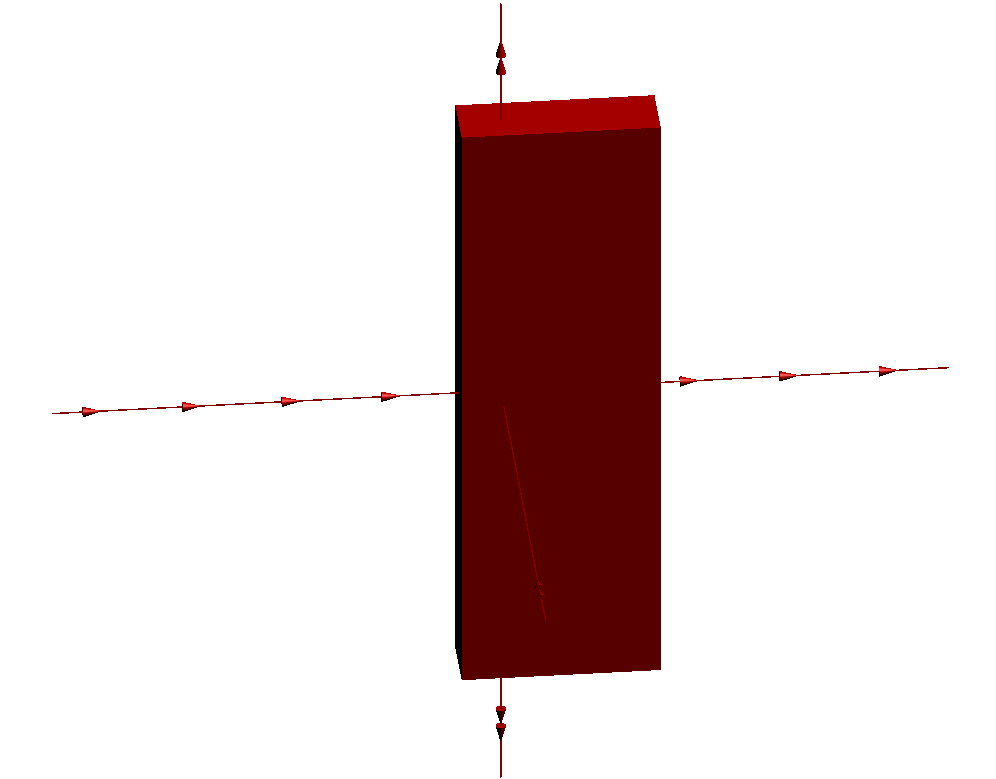
Maintenant au lieu d'utiliser un pavé, considérons la surface suivante en forme d'éventail, obtenue en assemblant deux demi-cônes "longs et fins" et deux demi-cônes "larges et plats", selon une configuration de "balle de tennis" :

(Pour rendre l'animation suivante plus symétrique, j'ai en fait utilisé ici des cônes elliptiques plutôt que des cônes circulaires.) Lorsque g agit sur cette surface, elle aplatit les demi-cônes longs et fins, et les rend larges et plats ; et elle étire au contraire les demi-cônes larges et plats, les rendants longs et fins :

Remarquez aussi qu'au passage, aussi incroyable que cela puisse paraître étant donné que g est une application affine, elle retourne la surface comme une chaussette ; elle envoie toute la région de l'espace qui se trouve a l'extérieur de la surface originelle dans la région de l'espace qui est renfermée par la surface image :

(Bien sûr ce comportement contre-intuitif est rendu possible par le fait que la surface n'est pas convexe.)

Considérons maintenant une deuxième application affine h, qui est définie d'une façon similaire à g mais en utilisant une autre base. On peut alors schématiser la situation de la façon suivante ; tandis que g envoie la surface rouge sur la surface rouge, h envoie la surface verte sur la surface verte :

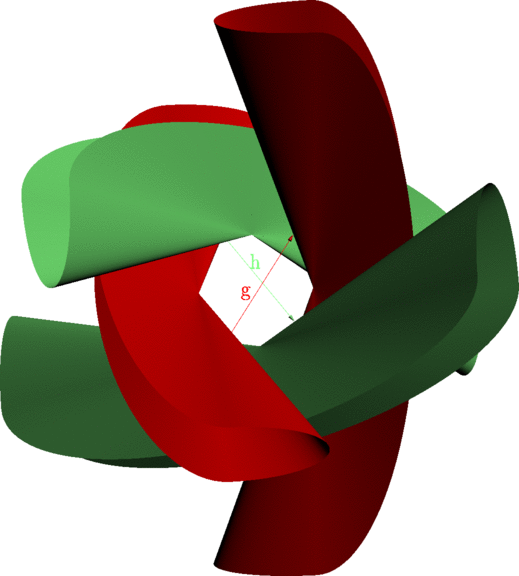
Observons maintenat (c'est là un point clé) que les quatre surfaces sont disjointes. Cela montre que le groupe engendré par g et h vérifie le lemme du ping-pong ; il est donc libre et agit proprement sur R³, avec pour domaine fondamental le complément des quatres régions "renfermées" par les quatre surfaces. La situation est assez similaire à celle d'un groupe de Schottky classique. En appliquant successivement tous les éléments du groupe au domaine fondamental, on obtient un pavage affine de R³, dont le graphe dual est un arbre (le graphe de Cayley du groupe libre en deux générateurs). Voici le début de ce pavage, comprenant cinq tuiles (la tuile "centrale" et ses images par les deux générateurs et leurs inverses) :