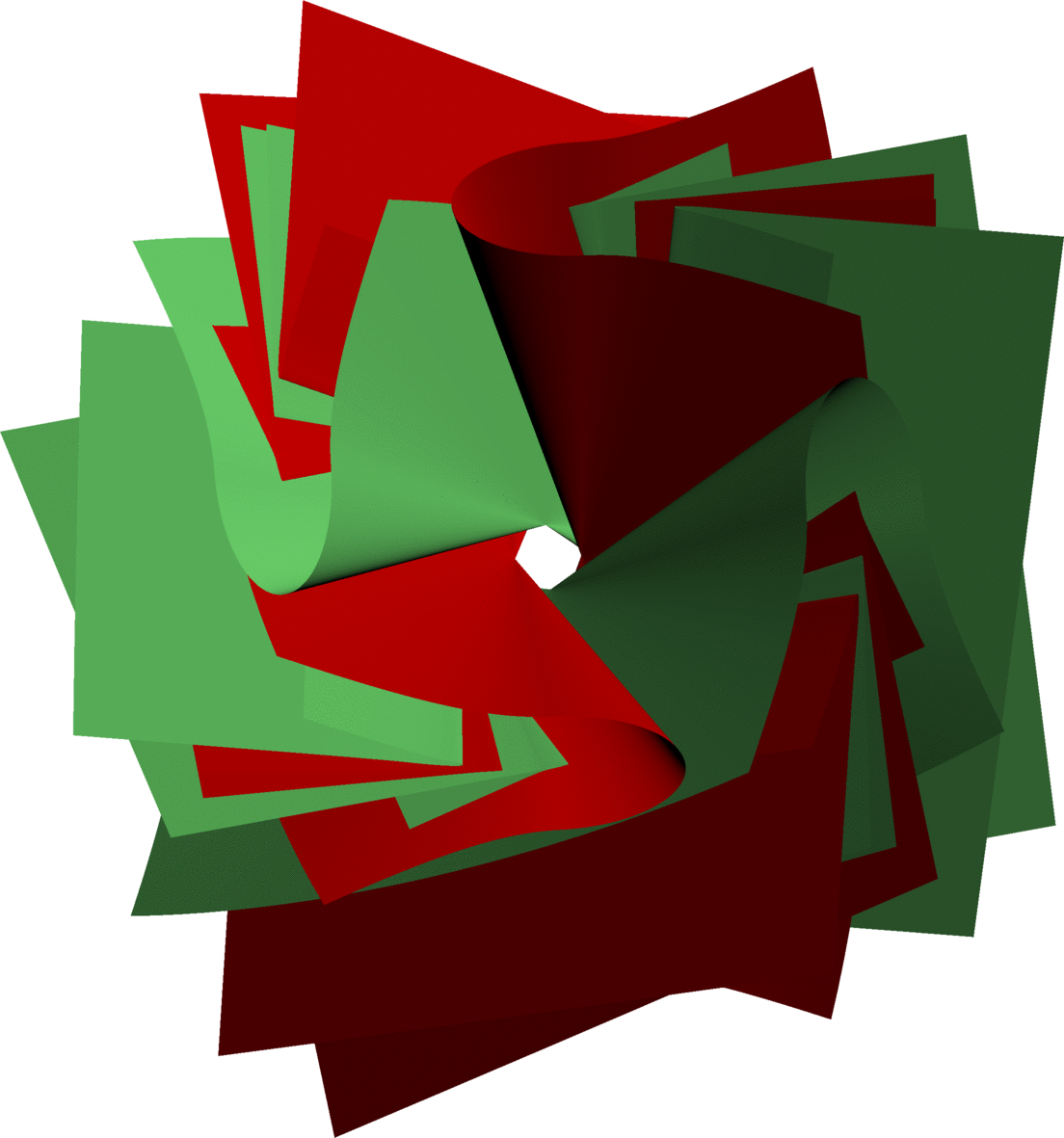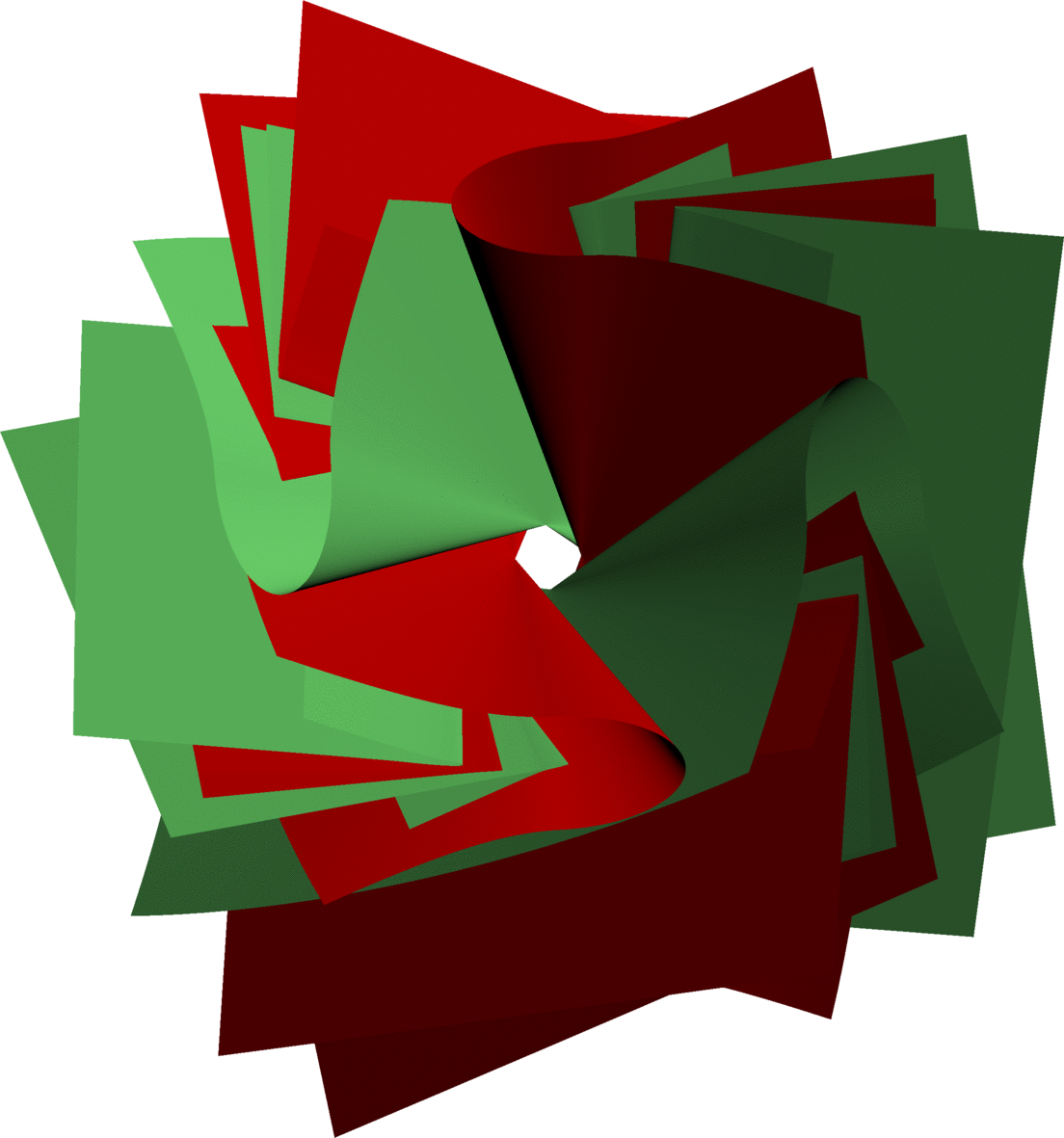Ilia Smilga: Quick introduction to free groups of affine transformations acting properly
 Homepage
Homepage  Page d'accueil
Page d'accueil
Consider an affine transformation g of R3 defined as follows:
- it multiplies all lengths in the z direction by some constant λ>>1;
- it divides all lengths the y direction by the same constant λ;
- and it translates by some fixed length along the x direction.
Here is the action of this transformation g on a parallelepiped:
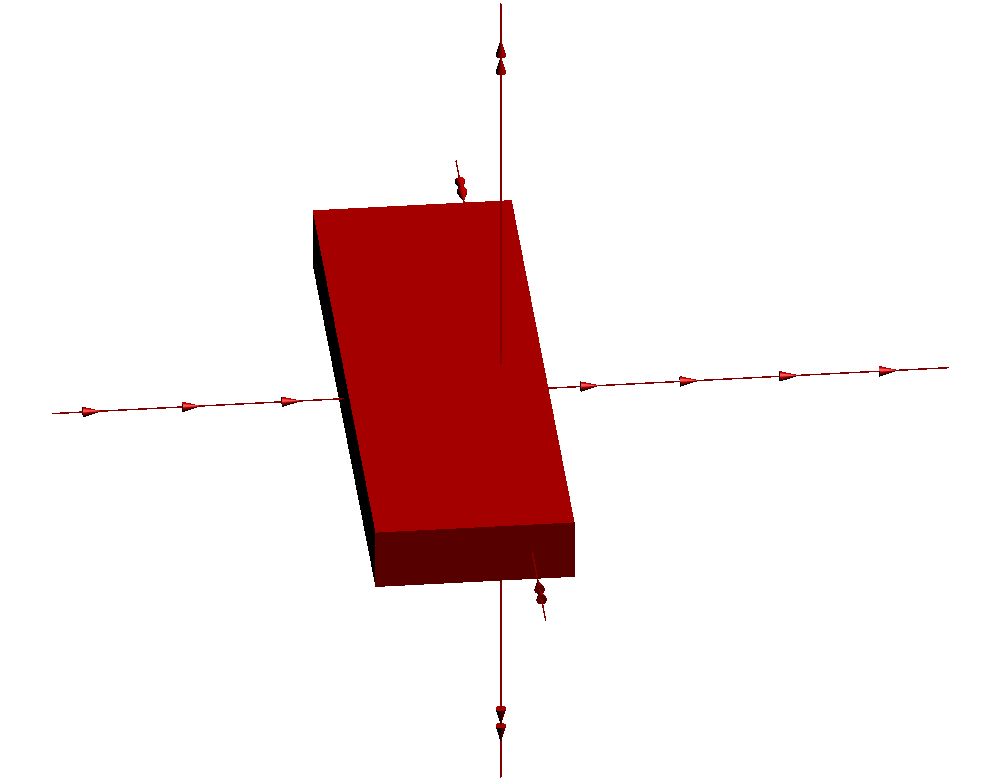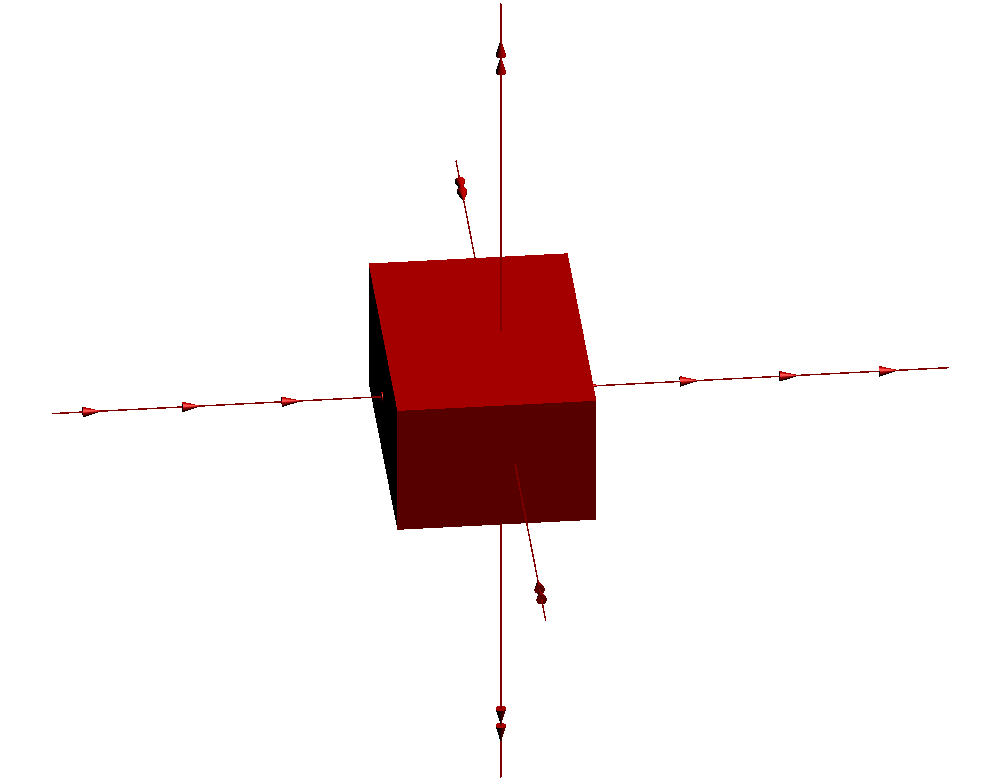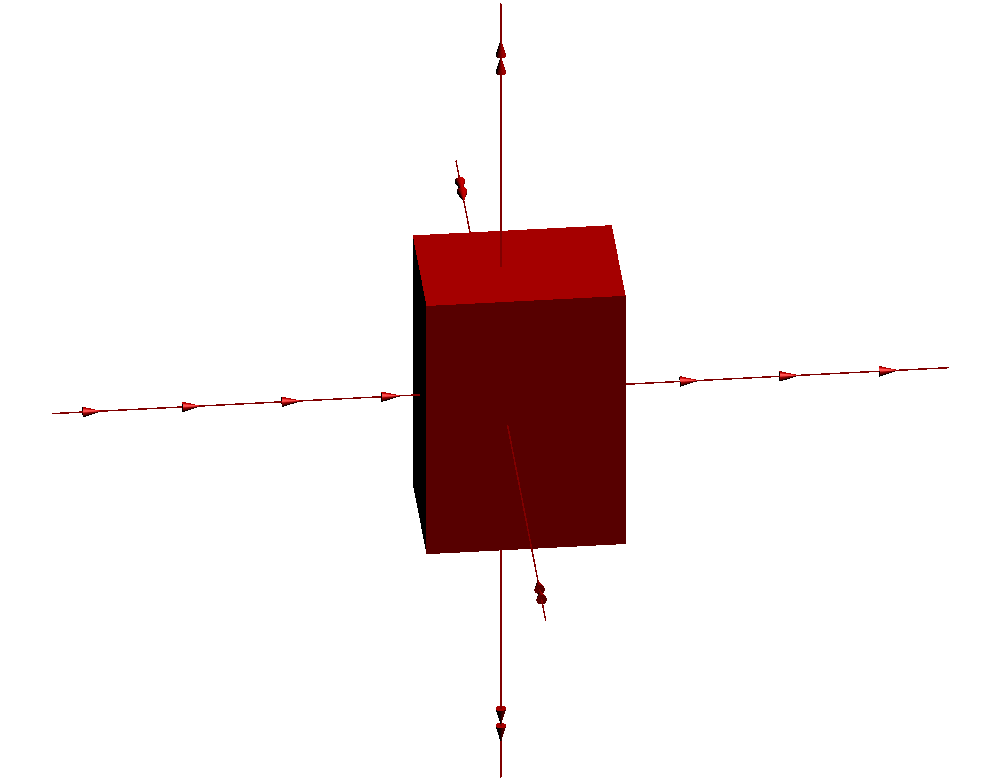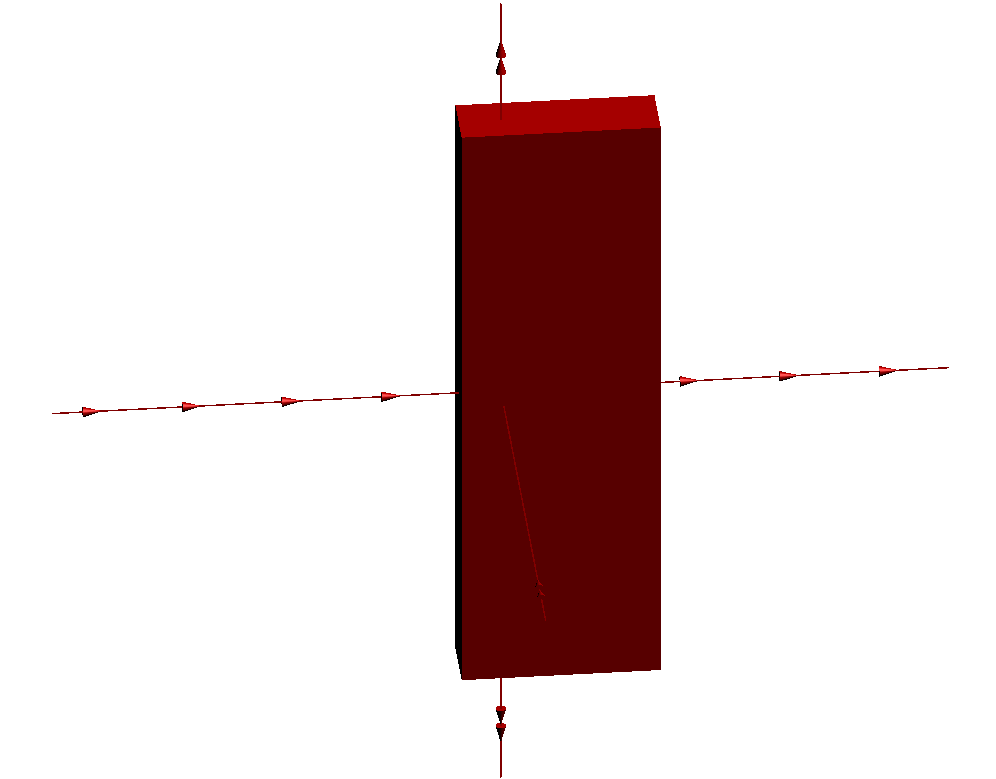
Now instead of using a parallelepiped, consider the following fan-shaped surface, made by gluing together two "long and thin" half-cones and two "broad and flat" half-cones in a "tennis ball" pattern:

(To make the pictures more symmetric, I actually used elliptic rather than circular cones.) When g acts on this surface, it flattens the long and thin half-cones, making them broad and flat; and stretches the broad and flat half-cones, making them long and thin:

Also note that in the process, as incredible as it is given that g is an affine map, it turns the surface inside out; it sends the entire region of space lying outside the original surface into the region of space enclosed by the image of the surface:

(Of course the explanation of this counter-intuitive behavior lies in the fact that the surface is not convex.)
Now let us consider another affine map h, which is defined in a similar way to g but using another basis. Then we have the following picture; whereas g maps the red surface onto the red surface, h maps the green surface onto the green surface:
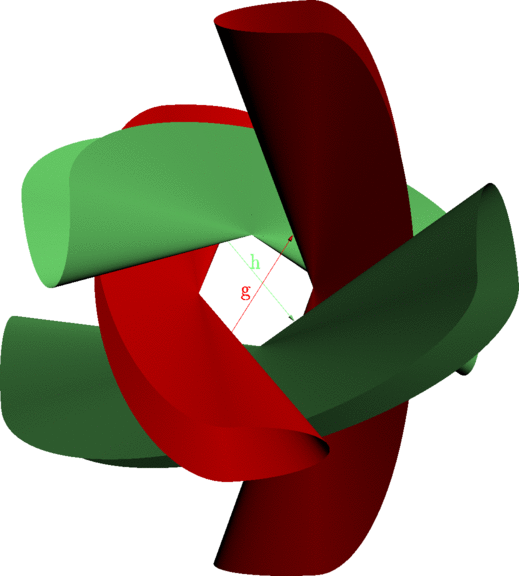
Now observe (this is a crucial point) that all four surfaces are disjoint. This shows that the group generated by g and h satisfies the ping-pong lemma; hence it is free and acts properly on R3, with fundamental domain equal of the complement of the four regions "enclosed" by the four surfaces. The situation is quite similar to a classical Schottky group. Applying all elements of the group to the fundamental domain, we get an affine tiling of R3, whose dual graph is a tree (the Cayley graph of the free group on two generators). Here is the beginning of this tiling, comprising five tiles (the "central" tile and its images by both generators and their inverses):