let succ x = x + 1;;
val succ : 'a int -> 'a int |



flowcaml command from the shell. Under the interactive
toplevel, the user types Flow Caml phrases, terminated by ;;,
in response to the # prompt. The system type-checks them on the
fly and prints the inferred type scheme.
let x = 1;;
x : 'a int |
x to the integer constant 1. The toplevel answers that
this constant has type 'aint. In Flow Caml, the type
constructor int takes one argument, which is a security
level belonging to an arbitrary lattice. These annotations allow
the system to trace information flow. In the above example, the
security level is a variable, 'a; as every variable appearing
free in a type, it is implicitly universally quantified. Basically,
this means that outside of any context, the constant 1 may have
any security level.
let x1 : !alice int = 42;;
val x1 : !alice int
let x2 : !bob int = 53;;
val x2 : !bob int
let x3 : !charlie int = 11;;
val x3 : !charlie int |
!alice, !bob or !charlie (Any
alphanumeric identifier preceded by a ! is a suitable constant
security level.) Initially, these security levels are incomparable
points in the lattice: this means that the principals they represent
cannot exchange any information. We will further on see how to allow
some (see section 2.6).
x1 + x1;;
- : !alice int
x1 + x2;;
- : [> !alice, !bob] int
x1 * x2 * x3;;
- : [> !alice, !bob, !charlie] int |
x1, so
its security level is !alice. The sum x1 +x2 is liable
to leak information about x1 and x2. Then, its security
level must be greater than those of x1 and x2:
[> !alice, !bob] stands for any level which is greater than or
equal to !alice and !bob. This can be read as the
``symbolic union'' of these two principals. Similarly, the
security level of the last expression must be greater than or equal to
!alice, !bob and !charlie.
let succ = function x -> x + 1;;
val succ : 'a int -> 'a int |
'a int -> 'aint. This type means
that the function succ takes as argument one integer of some
level 'a and returns another integer whose security level is
exactly the same: indeed the result of this function carries
information about its input. Because its type is polymorphic w.r.t.
the security level of the integer argument, you can apply succ
on arguments of different levels:
succ x1;;
- : !alice int
succ x2;;
- : !bob int |
succ for every level it is
used with.
let half = function x -> x lsr 1;;
val half : 'a int -> 'a int |
half is exactly the same as that of
succ: it reflects that the result produced by half reveals
some information about its input. However, this leak is only partial,
because it is, for instance, not possible to completely retrieve
x1 from the result of halfx1. In some situations, this
may yield typings which are surprising at first sight:
let return_zero = function x -> x * 0;;
val return_zero : 'a int -> 'a int |
return_zero always returns zero! Roughly speaking, this
is because for the system, the result of a product always leaks
information about the two factors, whatever they are. Obviously, if
you rewrite the function as follows:
let return_zero' = function x -> 0;;
val return_zero' : 'a int -> 'b int |
'b) is not related to that of the input ('a),
reflecting the absence of information flow from the latter to the former.
return_zero x1;;
- : !alice int
return_zero' x1;;
- : 'a int |
int, the
corresponding type constructors carry one security level:
let y0 = true;;
- : 'a bool
let z0 = 'a';;
val z0 : 'a char |
let pi = 3.14159265359;;
val pi : 'a float
let pi' = 4.0 *. atan 1.0;;
val pi' : 'a float |
string) mutable ones (type charray). One
may wonder why we distinguish them, since in Objective Caml every
string is mutable---even if it is not used as such---and everything
works well. This design choice is motivated because, in type systems
tracing information flow, mutable values require some particular care
which increases the complexity of types (we will discuss this point in
section 2.3) whereas, in many situations,
strings are used without in place modification. Hence, providing a
distinct type for such cases allows better typings.
let s = "Flow Caml";;
val s : 'a string |
string and it has one argument which is a
security level. It naturally describes all information attached to
the string. The module String provides functions for manipulating
immutable strings.'a, 'b, etc. we have encountered in
type schemes up to now stand for levels of the security
lattice. In Flow Caml, polymorphism applies naturally on whole types
(as in Objective Caml) too. For instance, define the identity
function:
let id x = x;;
val id : 'a -> 'a |
'a stands for a type. Indeed, in
Flow Caml, a variable appearing in a typing can be of different kinds:
it may stand either for a level or for a type (in
section 2.4, we will see it also may
denote a row). What is more, kinds are not given explicitly
by the system (and the programmer does not have to give them when he enters
a type expression) because they always can be deduced from the
context. The type scheme inferred for id does not involve any
security annotation: it simply says that the function takes an
argument of some type 'a and produces a result of the same type.
For instance, if you specialize the identity function so that it
applies only to integers, it will have the type
'b int -> 'bint.list type constructor has two arguments
(while in Objective Caml it has only one). Thus, in the type
('a, 'b)list, 'a is a type variable
which gives the type of the elements of the list; 'b is a
level variable describing the information attached to the
structure of the list. This corresponds for instance to the
information leaked by testing whether the list is empty.
let l1 = [1; 2; 3; 4];;
val l1 : ('a int, 'b) list
let l2 = [x1; x2];;
val l2 : ([> !alice; !bob] int, 'b) list |
let is_empty = function [] -> true | _ :: _ -> false ;;
val is_empty: ('a, 'b) list -> 'b bool |
'b does not depend on the type of the list's
elements, 'a, but is the same as the level of the input list, because
the function reveals information only about its structure of the list.
Functions manipulating lists are often recursive, but this does not
raise any particular difficulty concerning typing:
let rec length = function [] -> 0 | _ :: tl -> 1 + length tl ;;
val length: ('a, 'b) list -> 'b int |
length is similar to that of
is_empty: the length of the list contains some information about
its structure, but not about its elements. On the contrary, a function
testing whether the integer 0 appears in a list reveals
information about both the structure of the list and its elements,
hence its type:
let rec mem0 = function [] -> false | hd :: tl -> hd = 0 || mem0 tl ;;
val mem0: ('a int, 'a) list -> 'a bool |
List of the standard library provides usual functions
operating on lists, including the following examples:
let rec rev_append l1 l2 = match l1 with [] -> l2 | hd :: tl -> rev_append tl (hd :: l2) ;;
val rev_append: ('a, 'b) list -> ('a, 'b) list -> ('a, 'b) list
let rev l = rev_append l [];;
val rev: ('a, 'b) list -> ('a, 'b) list |
None (the empty option) or Somev, where v is
another value, the content of the option. The type
option behaves similarly to that of lists. It has two arguments
too: in ('a, 'b)option, 'a is the type of the content of
the option while 'b is the security level attached to the option
itself, describing the information attached to the knowledge of its
form. This is illustrated by the following functions:
let is_none = function None -> true | Some _ -> false ;;
val is_none: ('a, 'b) option -> 'b bool |
is_none tests whether an option is None, by a
simple pattern matching. Thus, the security level of the obtained
integer is exactly that of the option: the test is likely to leak
information only about the form of the argument.
let default = function None -> 0 | Some x -> x ;;
val default: ('a int, 'a) option -> 'a int |
default matches an integer option. If it is
None, it returns the default value 0, and otherwise the
content of the option itself. Thus, the result produced by an
application of default carries information about both the form of
the option and its content.x1, ..., xn are values whose respective types are
t1, ..., tn then (x1, ..., xn) is a tuple of
type t1 * ... *tn. For instance:
let pair0 = (0, true);;
val pair0 : 'a int * 'a bool
let triple0 = (0, 1, 'a');;
val triple0 = 'a int * 'a int * 'a char |
!alice and the second !bob :
let pair1 = x1, x2;;
val pair0 : !alice int * !bob int |
f1 takes one integer x as argument and
returns a pair formed of its successor and its sum with the global
constant x1 defined above:
let f1 x = (x + 1, x + x1);;
val f1 : 'a int -> 'a int * 'b int with 'a < 'b and !alice < 'b |
'a and 'b. The first one, 'a, is the security level
of the function's argument. Naturally, it is also that of the first
component of the pair returned by the function. The second integer
returned by the function is labeled by the variable 'b. This
security level is related to 'a by the first inequality
appearing after the keyword with: 'a < 'b tells us that
'b must be greater than or equal to 'a (note that the
character < output by your terminal stands, in Flow Caml, for
the mathematical symbol £). In what concerns information flow,
this inequality reflects the fact that the integer labeled by 'b
depends on the one labeled 'a; in other words that there is a
flow from the latter to the former. The other constraint,
!alice < 'b requires 'b to be greater than or equal to
the constant !alice. It says that there is a possible flow from
data (namely x1) coming from the external source symbolized by
the constant !alice (the principal Alice) to the
second output of the function.
f1 0;;
- : 'a int * !alice int
f1 x1;;
- : !alice int * !alice int
f1 x2;;
- : !bob int * [> !alice, !bob] int |
f1 means that every instance of 'a int -> 'a int * 'bint
for some 'a and 'b which satisfy the inequalities
'a < 'b and !alice < 'b
is a valid type for the function. This statement cannot be expressed
as precisely in a unification-based type system. Indeed, in such a
framework, every < must be read as =, i.e. the variables
'a and 'b must be unified with the constant !alice.
Thus we would obtain the following judgment:
val f1 : !alice int -> !alice int * !alice int |
f1 to the integer 0 would yield a result of type
!aliceint (instead of 'aint), while the expression
f1x2 would be ill-typed. The same observation can be made with
the following function, f2, which takes three integer arguments
and computes the sums of each pair of them:
let f2 x y z = (x + y, y + z, x + z) ;;
val f2 : 'a int -> 'b int -> 'c int -> 'd int * 'e int * 'f int with 'a < 'd, 'f and 'b < 'd, 'e and 'c < 'e, 'f |
'a < 'd, 'f (which is a shorthand for
'a < 'd and 'a < 'f) traces the information flow from the first
argument, x to the first and third components of the result,
x +y and x +z respectively. The next two constraints
deal similarly with the second and third arguments of the function,
respectively. Obviously, the system performs some arbitrary choice
when it typesets a list of constraints. For instance, f2's scheme
may equivalently be written:
val f2 : 'a int -> 'b int -> 'c int -> 'd int * 'e int * 'f int with 'a, 'b < 'd and 'b, 'c < 'e and 'a, 'c < 'f |
x1, x2
and x3, the constraints allow to compute the respective levels
of the resulting integer:
f2 x1 x2 x3;;
- : [> !alice, !bob] int * [> !bob, !charlie] int * [> !alice, !charlie] int |
f2 would have a much more restrictive typing
val f2 : 'a int -> 'a int -> 'a int -> 'a int * 'a int * 'a int |
<, which is
said to be a subtyping order. In general terms, subtyping
consists of a partial order on types and a subsumption rule that
allows every expression which has a given type to be used with any
greater type, i.e. if an expression e has some type t and t is
a subtype of t' (t < t') then e also has
type t'. In Flow Caml, subtyping is structural and defined by
lifting the order between security levels throughout the structure of
types: two comparable types must have the same ``structure'' and only
their annotations may differ. For this purpose, every type
constructor (such as int, list or ->) has a
signature which gives the variance (and the kind) of each of
its argument. A variance is either + (covariant),
- (contravariant) or = (invariant). The
signature of a type constructor can be displayed in the toplevel
thanks to the directive #lookup_type:
#lookup_type "int";;
type (#'a:level) int |
'a) of int is a level
and is covariant. (The # symbol is a distinguished form of
+, whose role will be explained in
section 2.2.2. For the time being, you can
simply read it as if it were +.) This defines the subtyping
order on integer types: given two security levels 'a and
'b, 'a int < 'bint holds if and only if
'a < 'b. Similarly, the two arguments of list are
also covariant:
#lookup_type "list";;
type (+'a:type, #'b:level) list = ... |
('a1, 'b1) list < ('a2, 'b2)list
is equivalent
to 'a1 < 'a2 and 'b1 < 'b2. As a result, subtyping constraints
involving two type structures can be decomposed recursively: for
instance ('a1 int, 'b1) list < ('a2 int, 'b2)list produces
'a1 int < 'a2int and 'b1 < 'b2 and then
'a1 < 'a2 and 'b1 < 'b2.f3 takes three arguments and build three lists of two
elements each:
let f3 x y z = ([x; y], [y; z], [x; z]) ;;
val f3 : 'a -> 'b -> 'c -> ('d, 'e) list * ('f, 'g) list * ('h, 'i) list with 'a < 'd, 'h and 'b < 'd, 'f and 'c < 'f, 'h |
f2. Each constraint relates the type of one input to those of
the result: thus, the type of the first argument, 'a is
``injected'' in those of the elements of the first and third lists,
reflecting the dependency. However, it is worth noting that here, the
variables 'a, 'b, 'c, 'd, 'e and
'f are types, not levels.-> we have encountered in the
previous examples has the following signature:
type (-'a:type) -> (+'b:type) |
'a1 -> 'b1 £ 'a2 -> 'b2 holds
if and only if 'b1 £ 'b2 and 'a2 £ 'a1.+. In the Flow Caml standard library, it is declared
with the following scheme:
val ( + ) : 'a int -> 'a int -> 'a int |
x1 + x2;;
- : [> !alice, !bob] int |
x1 has the type !aliceint. By
subsumption, it can be freely used with any greater type, e.g.
[> !alice, !bob]int. (The system is able to perform the
coercion itself when needed, no explicit annotation is therefore required.)
Similarly, x2 has type
!bobint but it can also be used as a value of type
[> !alice, !bob]int. It follows that the expression
x1 +x2 is well-typed and produces a value of type
[> !alice, !bob]int. Generalizing this process, one may
naturally propose another type scheme for ( +), which
explicitly includes the subsumption mechanism:
val ( + ) : 'a1 int -> 'a2 int -> 'a3 int with 'a1, 'a2 < 'a3 |
'a can be
replaced by a fresh variable 'b with the constraint
'b < 'a (resp. 'a < 'b). Applying this principle to the
scheme
val ( + ) : 'a int -> 'a int -> 'a int |
val ( + ) : 'a1 int -> 'a2 int -> 'a3 int with 'a1 < 'a and 'a2 < 'a and 'a < 'a3 |
<,
val ( + ) : 'a1 int -> 'a2 int -> 'a3 int with 'a1 < 'a3 and 'a2 < 'a3 |
if ...
then ... else ..., which has the same semantics
as that of Objective Caml, as well as polymorphic comparison
primitives. As explained above, the type of boolean values carries
one security level:
let y1 : !alice bool = false;;
val y1 : !alice bool
let y2 : !bob bool = false;;
val y2 : !bob bool |
then and else. Hence, the type of the
former must be a super-type of the latter. For instance, in the simple
case where a conditional produces integers, this means that the
security level of the whole expression must be the union of those of
the two branches:
if y0 then x1 else x2;;
- : [> !alice, !bob] int |
x1 has type !aliceint, x2
has type !bobint, so the whole expression has type
[> !alice, !bob]int. The value produced by a conditional
also carries information about the result of the test. Hence, in
order to take in account this possible information flow, the security
level of the latter must guard the type of the former, this
means that its security level(s) must be greater than or equal to that
of the condition:
if y1 then 1 else 0;;
- : !alice int |
y1, has level
!alice; hence the result of the whole expression must have this
level too. Similarly, if a conditional evaluates to a tuple, the type
of each of its components must be guarded by the level attached to the
test:
if y1 then (x1, (true, 'a')) else (x2, (false, 'b'));;
- : [> !alice, !bob] int * (!alice bool * !alice char) |
int_of_bool simply
converts a boolean into an integer:
let int_of_bool x = if x then 1 else 0 ;;
val int_of_bool : 'a bool -> 'a int |
let choose y1 y0 x = if x then y1 else y0 ;;
val choose : 'a -> 'a -> 'b bool -> 'a with 'b < level('a) |
choose clearly depends on the value of
the boolean x, and hence must be guarded by its security level,
'b. However, it has the type of the two other arguments of the
function, y0 and y1, but this may be arbitrary. That is
the reason why this example involves a new form of constraint,
'b < level('a). (In [PS03], this is written
'b 
'a.) Let us first
remark that in this constraint 'b and 'a are variables of
different kinds: 'b stands for a security level while 'a
is a type. This constraint can be viewed as an inequality
delayed until the structure of the type 'a is known: roughly
speaking, it means that the topmost security level(s) of the type
'a must be greater than or equal to 'b. For instance, if
you instantiate 'a by 'a1int, the constraint is simply
decomposed as 'b < 'a1, but, if you instantiate 'a by
'a1 int * 'a2bool, it produces 'b < 'a1 and 'b < 'a2. To
illustrate how this decomposition mechanism works, one can consider
some partial applications of the function:
let choose1 y = choose 1 0 y;;
val choose : 'a bool -> 'a int
let choose2 y = choose (1, 1) (0, 0) y;;
val choose : 'a bool -> 'a int * 'a int |
'a is instantiated by
'a1int and the constraint 'b < level('a1 int) is
decomposed as 'b < 'a1. This yields the scheme
'b bool -> 'a1 int with 'b < 'a1 |
'a bool -> 'aint. In the second
example, 'a is instantiated by 'a1 int * 'a2int. The
constraint becomes successively
'b < level('a1 int * 'a2 int) 'b < level('a1 int) and 'b < level('a2 int) 'b < 'a1 and 'b < 'a2 |
'a bool -> 'a int * 'aint. Similarly, we can also consider
lists:
let choose3 y = choose [] [1;2] y;;
val choose3 : 'a bool -> ('b, 'a) list |
'a is instantiated
by ('a1, 'a2)list, which yields the constraint
'b < level(('a1, 'a2) list) that is decomposed into
'b < 'a2. level
must be decomposed? This information is retrieved from signatures: the
arguments on which level applies are those which are marked as
``guarded'' by a sharp symbol (#):
#lookup_type "int";;
type (#'a:level) int
#lookup_type "list";;
type (+'a:type, #'b:level) list = ... |
level applies on the single
argument of int while it considers only the second one of
list. It is worth noting that # is a distinguished form
of +, that means that guarded arguments are always covariant.= or <=. These operators can
be used to compare data structures of any type, so, in Objective Caml,
they have the following type
'a -> 'a -> bool |
'b.
Moreover, because, the result produced by the operator is liable to carry
information about the two compared values, 'b must be related to
the security levels which describe them, i.e. those that appear
within the type 'a. For instance, specialized
versions of the equality for integers, pairs of integers, lists of
integers and lists of pairs of integers should have the following type
schemes:
val eq_int : 'a int -> 'a int -> 'b bool with 'a < 'b val eq_int_pair : ('a1 int * 'a2 int) -> ('a1 int * 'a2 int) -> 'b bool with 'a1, 'a2 < 'b val eq_int_list : ('a1 int, 'a2) list -> 'b bool with 'a1, 'a2 < 'b val eq_int_pair_list : ('a1 int * 'a2 int, 'a3) list -> 'b bool with 'a1, 'a2, 'a3 < 'b |
val eq_int_ref : ('a1 int, 'a2) ref -> ('a1 int, 'a2) ref -> 'b with 'a1, 'a2 < 'b |
'a2 < 'b---and their contents, hence
'a1 < 'b.'b that labels
the boolean produced by the comparison must be greater than
or equal to every security level that appears in the type of
the arguments. This reflects how comparison applies recursively on
data-structures. Thus, in order to give a principal type to these
polymorphic operators, we need an additional form of
constraint, content('a) < 'b where 'a is a type and
'b is a level. (In [PS03], this is
written 'b 
'a.) This
constraint requires every security annotation of the type 'a to
be less than or equal to the security level 'b. For instance,
content('a1 int * 'a2 int) < 'b is equivalent to
'a1 < 'b and 'a2 < 'b while content('a1 ref, 'a2) < 'b stands for
'a1 < 'b and 'a2 < 'b. This definition mimics the
behavior of generic comparison operators which traverse data structures
recursively. Then, in Flow Caml, = and <= have the
following type:
val ( = ) : 'a -> 'a -> 'b bool when content('a) < 'b
val ( <= ) : 'a -> 'a -> 'b bool when content('a) < 'b |
mem which
searches whether an element is amember of a list:
let rec mem x = function [] -> false | hd :: tl -> (x = hd) || mem x tl ;;
val mem : 'a -> ('a, 'b) list -> 'b bool with content('a) < 'b |
let rec insert x = function [] -> [x] | hd :: tl -> (min hd x) :: insert (max hd x) tl ;;
val insert : 'a -> ('a, 'b) list -> ('c, 'b) list with 'a < 'c and content('a) < level('c)
let rec sort = function [] -> [] | hd :: tl -> insert hd (sort tl) ;;
val sort : ('a, 'b) list -> ('c, 'b) list with 'a < 'c and content('a) < level('c) |
f1 and
f2 are two functions, (f1 = f2) either returns true
(if the two functions have the same memory address) or raises an
exception in all other cases. Such an expression seems to have a very
limited interest and is not really used because it largely depends on
the implementation: for instance let f = fun x -> x in (f = f)
returns true while (fun x -> x) = (fun x -> x) raises an
exception. However, the Caml type system has no way to prevent such
calls from arising. The SML [MTHM97] dialect of ML
addresses these issues by introducing ``eq'' types, and hence
refuses at compile time any application of a comparison primitive to
values which (are likely to) contain closures. The same approach is
followed in Flow Caml, where non-eq types are marked by the
keywork noneq in their definition, and the constraint
content('a) < 'b cannot be satisfied if 'a is a
non-eq type. Hence, the following piece of code yields a type
error:
(fun x -> x) = (fun x -> x);;
Magic generic primitives cannot be applied on expressions of type ~a -> ~a |
let skel x y = if x = y then (); x ;;
val skel : 'a -> 'b -> 'a with 'a ~ 'b |
skel xy tests whether x equals y, then returns
x. In the case where the test succeeds, the function skel
does nothing particular, but it should for instance be possible to
replace () by an expression which performs side-effects, as we
will do in section 2.3.2. However, the
current function is sufficient to illustrate the need of
same-skeleton constraints. skel, x and y, will be required to be of the same type, in
order to allow comparing them: skel's principal type scheme would
be 'a -> 'a -> 'a. However, in Flow Caml, thanks to subtyping,
it is no longer necessary to require them to have exactly the same
type: indeed, they may have different security annotations, e.g. be
two integers of different security levels. Formally, if
x has type 'a and y has type 'b, it is
sufficient to require the existence of a super-type 'c of
'a and 'b (i.e. such that 'a < 'c and
'b < 'c). This is what expresses the ~ constraint.
Indeed, the above type scheme is equivalent to:
val skel : 'a -> 'b -> 'a with 'a < 'c and 'b < 'c |
'c is an extra type
variable. It is easy to check that such a 'c exists if and only if
'a and 'b are two types of the same shape or
skeleton i.e. differ only by their non-invariant security
annotations. ~ predicate is transitive and
associative (it is indeed the symmetric, transitive closure of <),
so that same-skeleton constraints which involve a common variable can
be merged, as in the following example:
let skel3 x y z = if x = y or y = z then (); x ;;
val skel3 : 'a -> 'b -> 'c -> 'a with 'a ~ 'b ~ 'c |
let pred x = x + 1;;
val pred : 'a int -> 'a int
let pred_or_succ y = if y then pred else succ;;
val pred_or_succ : 'a bool -> 'b int -{|| 'a}-> 'b int |
val pred_or_succ : 'a bool -> ('b int -{|| 'a}-> 'b int) |
pred or succ an application of pred_or_succ returns
naturally leaks information about the boolean given as argument. In
order to reflect this information flow, the type assigned to the
function returned by pred_or_succ comprises an additional
security level, 'a, printed inside the arrow symbol: it intends
to describe how much information is attached to the knowledge of the
function. For instance, an application of pred_or_succ with a
boolean of level !alice yields a function whose identity has
level !alice too:
pred_or_succ y1;;
- : 'a int -{|| !alice}-> 'a int |
(pred_or_succ y1) to some
integer, the result must be guarded by the level !alice, because
it allows determining whether the function was pred or succ
and hence the boolean y1.
(pred_or_succ y1) 0;;
- : !alice int
(pred_or_succ y1) x2;;
- : [> !alice, !bob] int |
'a -{'b | 'c | 'd}-> 'e |
'a and 'e are the types of the argument
expected by the function and the result it produces, respectively.
Furthermore, 'b and 'd are levels. The former is a
lower bound on the side effects performed by the function (it will be
introduced in section 2.3) while the latter
represents information about the function's identity, as explained
above. Lastly, 'c is a row describing the exceptions
the function may raise (we will detail its usage in
section 2.4). However, in order to
improve readability, Flow Caml does not print annotations on arrows
that carry no information, i.e. that are universally quantified and
unconstrained type variables. For instance 'a -> 'b is a
shorthand for 'a -{'c | 'd | 'e}-> 'b (where 'c, 'd
and 'e are fresh variables), while 'a -{|| 'b}-> 'c stands
for 'a -{'d | 'e | 'b}-> 'c (where 'd and 'e are
fresh). -graph option, or---at any time---by entering the following
directive in the toplevel:
#open_graph;; |
|
 |
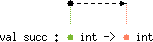
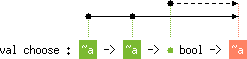
succ's type scheme, the dashed arrow from
the green bullet to the red one symbolizes an inequality whose left-
(resp. right-) hand-side is the security annotation symbolized by the
green (resp. red) bullet. Then, the drawing must be read as the
following scheme
val succ : 'a int -> 'b int with 'a < 'b |
'a int -> 'aint. Let us now
show how type variables are graphically represented.
|
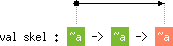 |
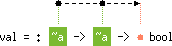
skel's
type scheme, the boxes labeled ~a stand for a skeleton
class: each occurrence of ~a must be read as a different type
variable a1, a2, ..., an, with the
constraint a1 ~ a2 ~ ... ~ an. For instance,
~a -> ~a -> ~a represents
'a1 -> 'a2 -> 'a3 with 'a1 ~ 'a2 ~ 'a3 |
'a1 < 'a3.
|
 |
|
 |
content('a) < 'b, 'a < level('b) and
level('a) < content('b), are drawn. All of them are
represented by a dashed arrow from (the box/bullet which stands for)
'a to (the box/bullet which stands for) 'b. No confusion
can arise thanks to kinding as illustrated by the following table:kind of 'a |
kind of 'b |
meaning of a dashed arrow from 'a to 'b |
|||||
level |
level |
'a |
< | 'b |
|||
level |
type |
'a |
< | level('b) |
|||
type |
level |
content('a) |
< | 'b |
|||
type |
type |
content('a) |
< | level('b) |
|||
|
 |
|
 |
choose, the dashed arrow symbolizes the
constraint 'b < level('a), while in that of ( =) it
stands for content('a) < 'b.while and for loops.
r := not y r := if y then false else true if y then r := false else r := true r := true; if y then r := false |
r, storing in it the negation of the boolean
y. Hence, this produces some information flow from y to
r. However, depending on the cases, it is of a different
nature. In the two first examples, the flow is said to be
direct: a value depending from y is computed and then
stored in r; this is very similar to what we have encountered up
to now. On the contrary, in the last two expressions, the value in
every right-hand-side of the := operator does not involve
y: it is even given explicitly in the source code. However,
the reference's update is performed in a branch of the program whose
execution is conditioned by the value of y. In this situation,
we say there is an indirect flow form y to r. The
last example calls for an additional comment: in the case where the
boolean y is false, the reference r is never updated
in a context conditioned by y. However, the information flow
from the latter to the former still exists: it is indeed possible to
leak information through the absence of a certain effect.
(This last example shows that it would be very difficult to
detect information flow at run time.)ref, has two
arguments:
#lookup_type "ref";;
type (='a:type, +'b:level) ref = ... |
ref is a security
level, which is guarded and covariant. It describes how much
information is attached to the identity of the reference, in
other words its memory address.r1 and r2 whose contents are declared to be
booleans of levels !alice and !bob, respectively.
let r1 : (!alice bool, 'a) ref = ref true;;
val r1 : (!alice bool, 'a) ref
let r2 : (!bob bool, 'a) ref = ref true;;
val r2 : (!bob bool, 'a) ref |
r1 has type
!alicebool. This means it may receive any boolean whose
security level is less than or equal to !alice, i.e. a boolean
Alice is allowed to read. The boolean y1 (defined in
section 2.1) has level
!alice. Hence it can legally be stored in r1:
r1 := y1;;
- : unit |
unit. Because there is only one value of this type, the
constant (), the value of a unit expression yields no
information. At a result, the unit type constructor does not
carry any security annotation. On the contrary, the boolean y2
has been declared with the level !bob. Because information flow
from !bob to !alice is not allowed (see
section 2.6), assigning it to
r1 raises a typing error:
r1 := y2;;
This expression generates the following information flow: from !bob to !alice which is not legal. |
r1 can be updated in a context whose
execution depends on y1 but not y2:
if y1 then r1 := false else r1 := true;;
- : unit
if y2 then r1 := false else r1 := true;;
This expression generates the following information flow: from !bob to !alice which is not legal. |
r1 naturally yields a boolean of
level !alice:
!r1;;
- : !alice bool |
if y1 (* y1 has type !alice bool *) then ... (* this branch is typechecked at level !alice *) else if y2 (* y2 has type !bob bool *) then ... (* this branch is typechecked at level [> !alice, !bob] *) else ... (* this branch is typechecked at level [> !alice, !bob] *) |
ref
appears when a reference is used as first class value, e.g. if it is
the result of some function. For instance, let
us define a version of the function choose specialized for
references by a type constraint:
let choose_ref y r1 r0 : (_, _) ref = if y then r1 else r0 ;;
val choose_ref : 'a bool -> ('b, 'a) ref -> ('b, 'a) ref -> ('b, 'a) ref |
y. Such an
observation can be performed, for instance, by updating its content.r1 to false:
let reset_r1 () = r1 := false ;;
val reset_r1 : unit -{!alice ||}-> unit |
!alice. This is reflected by the
annotation !alice printed ``inside'' the arrow symbol of the
above type: this security level is a lower bound on the effects
performed by the function and an upper bound on the contexts where it
can be applied. In many cases, it is a variable related to (parts of)
the type of the function's argument:
let reset r = r := false ;;
val reset : ('a bool, 'a) ref -{'a ||}-> unit |
reset takes a reference as argument and sets its
content to false. The type system constrains the level of the
content of the reference to be equal to or greater than (1) the level
attached to the reference's identity and (2) the level attached to the
context where the function is applied.y. This is reflected in the inferred scheme
by the fact that all of them are annotated by the same security level,
'a.length, in imperative style:
let length' list = let counter = ref 0 in let rec loop = function [] -> () | _ :: tl -> incr counter; loop tl in loop list; !counter ;;
val length' : ('a, 'b) list -{'b ||}-> 'b int |
length's type:
val length: ('a, 'b) list -> 'b int |
length', the result's security level must be greater than
or equal to the function's pc parameter. However, the
difference is only superficial; it can be checked that both types in
fact have the same expressive power.array)
carries two arguments:
[|0; 1; 2|];;
- : ('a int, 'b) array |
ref: the former is the type of the content of the cells of the
array, and the latter is a security level, related to the array
identity. A slight novelty is that this comprises information
attached to the length of the array. Indeed, the function returning
the length of an array has the following type:
Array.length;;
- : ('a, 'b) array -> 'b int |
[|'a'; 'b'; 'c'|];;
- : ('a char, 'b) array
"abc";;
- : ('a, 'b) charray |
charray expects two
security levels as arguments. The first one describes information
attached to the characters stored in the string while the second one
is related to the identity of the string (including its length).exception
construct and signaled with the raise operator:
exception X;;
exception X
exception Y;;
exception Y
raise X;;
- : 'a |
X in the above example) is not a value, and hence
cannot be bound to a variable or passed as argument to a function
(while in Objective Caml, it is a legal value of type exn).
Similarly, in Objective Caml, raise is a regular function which
accepts an arbitrary argument (of type exn), but, in Flow Caml,
it is a built-in construct which requires the name of the raised
exception to be statically specified. For instance, the following
Objective Caml piece of code cannot be written in Flow Caml:
let f x = raise (if x then X else Y) ;; |
let f x = if x then raise X else raise Y ;; |
try ...finally and try ...propagate
(see section 2.4.3).X: 'a; Y: 'b; 'c stands for the row which maps
the exception name X to 'a, Y to 'b and whose
other entries are given by 'c. Here, 'a and 'b are
levels while 'c is a row variable of domain
X,Y: it stands for a row ranging over all exception names except
X and Y. The order in which fields appear is not
significant: the above row is equal to Y: 'b; X: 'a; 'c. Row
variables can appear in constraints: the subtyping order is extended
point-wise to rows. Indeed, if 'c1 and 'c2 are two row
variables of the same co-domain, the constraint 'c1 < 'c2 means
that every entry of 'c1 must be less than or equal to the
corresponding one in 'c2. Hence, constraints involving expanded row
terms may be decomposed: X: 'a1; Y: 'b1; 'c1 < X: 'a2; Y: 'b2; 'c2
is equivalent to 'a1 < 'a2 and 'b1 < 'b2 and 'c1 < 'c2.
Lastly, for the sake of conciseness, when it prints a type scheme,
Flow Caml omits unconstrained universally quantified row variables:
for instance, A: 'a; Y: 'b stands for A: 'a; Y: 'b; 'c
where 'c is a fresh row variable.X:
let raise_X () = raise X ;;
val raise_X : unit -{'a | X: 'a |}-> 'b |
X: 'a, tells that the given function may raise an
exception of name X: catching this exception leaks information
about the context where the function is called, so the security level
associated to X is constrained to be at least that of the
context where the function is applied (which appears as usual in first
place in the arrow). In the following example,
let raise_X' y = if y then raise X ;;
val raise_X' : 'a bool -{'a | X: 'a |}-> unit |
X gives information about both the
context where raise_X' has been applied and the boolean
argument given to the function. Thus, the annotation associated to
the entry X in the row of this function must be greater than or
equal to the security levels of both.
let raise_X_or_Y x y = if x then raise X; if y then raise Y ;;
val raise_X_or_y : 'a bool -> 'b bool -{'a | X: 'a; Y: 'b |}-> unit with 'a < 'b |
X yields information
only about the first argument, x; while handling Y about
both.X if it is zero and returns false otherwise:
let test_zero x = if x = 0 then raise X; false ;;
val test_zero: 'a int -> {'a | X: 'a |}-> 'b bool |
false. However,
this function can reveal information about its argument through its
effect. This is reflected by the security level associated to
the exception X in its type: it must be greater than or equal to
the levels of the context where the function is applied and the integer
argument. try ...with construct.
try test_zero x1 with X -> true ;;
- : !alice bool |
test_zerox1 is liable to raise an exception
X with the level !alice, which will be catched by the
handler try ... with X->. Thus, the value produced by the
whole construct must be guarded by the level of the handled
exception, i.e. !alice. Let us embed this piece of code in a
function:
let f5 x = try test_zero x with X -> true ;;
- : 'a int -{'a ||}-> 'a bool |
f
carries information about its argument, but also about the context
where the function is called although it does not. However, we
witness the same phenomenon as for side effects: once again this is
only a superficial difference with the typing obtained for the
function written in a direct style:
let f6 x = if x = 0 then true else false ;;
val f6 : 'a int -> 'a bool |
with part is actually a kind of pattern-matching on
exception names (however, this is not a regular pattern matching since
exceptions are not values). In particular, one try ..with
construct can catch several exceptions names (or even all of them
using the _ pattern), as illustrated by the following example:
let f7 x y = try raise_X_or_Y x y; 0 with X -> 1 | Y -> 2 ;;
val f7 : 'a bool -> 'a bool -{'a ||}-> 'a int |
Division_by_zero when its second argument is zero, as
reflected by its type:
val ( / ) : 'a int -> 'b int -{'c | Division_by_zero: 'c |}-> 'a int with 'b < 'c, 'a |
Division_by_zero.
This reflects that this operator does not need to match its first
argument before raising the exception.
let f8 x y = (if x = 0 then raise X else x) + (if y = 0 then raise Y else y) ;;
val f8 : 'a int -> 'b int -{'c | X: 'd; Y: 'e |}-> 'f int with 'b < 'd, 'e, 'f and 'c < 'd, 'e and 'a < 'd, 'f |
y =0 is
considered before x =0, so the exception X carries
information about x and y while Y only about
y. Assuming a left-to-right evaluation order, one would obtain
the following scheme, where the roles of the variables 'a and
'b are exchanged:
'a int -> 'b int -{'c | X: 'd; Y: 'e |}-> 'f int with 'b < 'd, 'f and 'c < 'd, 'e and 'a < 'd, 'e, 'f |
f8 would be much less informative
about the function:
'a int -> 'a int -{'b | X: 'b; Y: 'b |}-> 'a int with 'a < 'b |
test_zero x1;;
- : 'a bool Current evaluation context has level !alice |
x1 is zero, evaluating this toplevel phrase
causes the program to terminate. Hence, if this does not happen and
execution continues, the remaining expressions receive some
information about x1 when they are evaluated. Therefore, they
must be type-checked in a context augmented with the security level of
the information carried by x1, i.e. !alice. This point
is expressed by the second line output by the system. Thus, all
side-effects performed afterward by the program must affect data of
levels greater than or equal to !alice. For instance, the
reference r1 (whose content has level !alice) can be
updated while r2 (whose content has level !bob) cannot:
r1 := false;;
- : unit
r2 := false;;
This expression is executed in a context of level !alice but has an effect at level !bob. This yields the following information flow: from !alice to !bob which is not legal. |
test_zero with x2, the level of
the toplevel context is increased by !bob:
test_zero x2;;
- : 'a bool Current evaluation context has level !bob, !alice |
r1 can no longer be updated,
because information flow from !alice to !bob is not
allowed (i.e. !alice is not inferior to !bob).
#reset_context;;
Level of evaluation context reset |
; operator. Let us for
instance consider the following function:
let f9 x r = if x = 0 then raise X; r := false ;;
val f9 : 'a int -> ('b bool, 'b) ref -{'a | X: 'a |}-> unit with 'a < 'b |
f9 takes two arguments: an integer x and a boolean
reference r. If the integer is 0 then the exception
X is raised, and the following statement is not performed.
Otherwise, execution continues and the reference r is set to
false. We now explain the typing inferred by the system, which
reflects the two possible observable effects of the function. First
of all, it may raise the exception X. The security level
attached to this effect, 'a, must be greater than or equal to
that attached to the context where the function is applied and that of
the integer argument, because the exception raising is conditioned by
a test on x. The second effect that the function is liable to
have is the update of the reference r. Observing it
gives information naturally about the context where f has been
called, but also reveals whether the exception X has been raised,
and, as a consequence, about the integer x. That is the reason
why, the security level of the content of the reference, 'b,
must be greater than the levels of the context where the expression is
applied and the first argument, as reflected by the constraint
'a < 'b.f9 into the following, the inferred type scheme
is similar:
let f10 x r = try if x <> 0 then raise X; () with X -> r := false ;;
val f10 : 'a int -> ('a bool, 'a) ref -{'a ||}-> unit |
r :=false is increased by the
security level associated to X in the expression between
try and with.try ...with, Flow Caml features
two other ways of handling expressions. Two reasons have motivated
their introduction: firstly, they partially counterbalance the loss of
expressiveness resulting of our decision to make exception names
second-class citizens; secondly, they allow a more precise typing
(w.r.t. information flow) of common idioms.with part of a try ...with
may be terminated by the keyword propagate. In this case, the
exception trapped by the handler is re-raised at the end of its
execution. For instance:
try e with X | Y -> e'; propagate |
e. If it raises X or Y then e' is
executed and, then, the trapped exception, X or Y, is
raised again. In Objective Caml, this can be implemented by binding
the exception to an identifier:
try e with X | Y as x -> e'; raise x |
e. In particular, two different levels may be associated to
X and Y.try ...finally construct of Flow Caml is a translation of
the Java's construct for the Caml language. Indeed
try e1 finally e2 |
e1, which yields either a regular value or an
exception. In both cases, e2 is executed, and the
result produced by e1 is returned. Once again, this can be
encoded in regular Caml (without even using exception values):
try let r = e1 in e2; r with exn -> e2; raise exn |
e2 does not raise any exception). However, using the
dedicated construct try ... finally allows better typings
(w.r.t. information flow): this makes explicit that the expression
e2 is always executed (whether e1 raises an
exception or not). Thus, the type system is able to take this in
account and type-checks e2 in a context whose level is not
altered by those of the exceptions possibly raised by e1,
whereas, in the proposed encoding, it is. For instance the
following piece of code is accepted by the type system:
try if y1 then raise X finally r2 := false ;; |
try if y1 then raise X; r2 := false; with _ -> r2 := false; propagate ;; |
exception Error of int;; |
ErrorAlice which is parameterized
by an integer of level !alice:
exception ErrorAlice of !alice int;; |
!alice as argument:
raise (ErrorAlice 0);;
raise (ErrorAlice x1);; |
ErrorAlice with an argument whose level is, for
instance, !bob. Obviously, a workaround may consist in defining
another exception name:
raise (ErrorAlice x2);;
This expression generates the following information flow: from !bob to !alice which is not legal.
exception ErrorBob of !bob int ;;
raise (ErrorBob x2);; |
exception Error : 'a of 'a int;; |
let error code = raise (Error code) ;;
val error: 'a int -{'a | Error: 'a |}-> 'b |
Error in the row
of this function combines two pieces of information: first, the
security level of the context where the exception is raised and, that
of the integer argument. Merging these two annotations into a
single one is relatively ad hoc; however, this allows keeping
concise typings, and works well with most common usage
of exceptions with arguments. It should be possible to provide a more
flexible mechanism for parameterizing types of exceptions arguments,
for instance by allowing several security levels as arguments, which
will also appear in rows. However, this would increase the complexity
of the system, as well as the verbosity of function types.Out_of_memory
and Stack_overflow which are respectively raised by the garbage
collector when there is insufficient memory to complete the
computation and the bytecode interpreter when the evaluation stack
reaches its maximal size. Indeed, analyzing them with Flow Caml would
be of little sense, because, in absence of sophisticated memory and
stack analyzes, one must assume them to be possibly raised at almost
every point of the program. That is the reason why they are not
provided in Flow Caml library: thus, they cannot be catched by
programs and become fatal errors.
#reset_context;; |
type declaration. First and foremost, this allows to define new
data structures using records and variants. The mechanism used to
define types in Flow Caml is similar to that of Objective Caml.
However, type declarations involve additional information, in
order to deal with the extra features of the type system related to
the security analysis.
type 'a cardinal = North | West | South | East # 'a ;;
type (#'a:level) cardinal = North | West | South | East # 'a |
cardinal (which is one of the four symbolic constants listed in
the declaration) is described by one security level, similarly to the
built-in enumerated types, such as integers or characters. Indeed, the
type constructor cardinal has one argument which is a security
level. In the above definition, this argument, 'a, is declared
to be the information level related to the sum by the clause
# 'a.#'a:level means that 'a is
a parameter of kind level, is covariant and must be guarded.
let p0 = North;;
val p0 : 'a cardinal
let p1 : !alice cardinal = North;;
val p1 : !alice cardinal
let p2 = if y2 then North else South;;
val p2 : !bob cardinal |
rotate, which takes as argument a
cardinal point and returns its successor in the clockwise order:
let rotate = function North -> East | West -> North | South -> West | East -> South ;;
val rotate: 'a cardinal -> 'a cardinal |
type ('a, 'b) option = None | Some of 'a # 'b ;;
type (+'a:type, #'b:level) option = None | Some of 'a # 'b |
('a, 'b)option: it is either the constant None or the
constructor Some with some argument of type 'a. The
fourth line of the declaration, # 'b tells that 'b is the
security level attached to the knowledge of the form of the option,
i.e. whether it is None or Some. (Let us recall that,
in the second case, information carried by Some's argument
is reflected by the security levels appearing in the type 'a
itself.)option: +'a:type means
that the first argument is covariant and is a type; while
#'b:level means that the second argument is a level, and is
covariant and guarded.list is naturally recursive; but this
has no particular consequence and the declaration is therefore similar
to the previous one:
type ('a, 'b) list = [] | :: of 'a * ('a, 'b) list # 'b ;;
type (+'a:type, #'b:level) list = [] | (::) of 'a * ('a, 'b) list # 'b |
type ('a, 'b) tree = Leaf | Node of ('a, 'b) tree * 'a * ('a, 'b) tree # 'b ;;
type (+'a:type, #'b:level) tree = Leaf | Node of ('a, 'b) tree * 'a * ('a, 'b) tree # 'b |
let rec height = function Leaf -> 0 | Node (tl, _, tr) -> max (height tl) (height tr) ;;
val height: ('a, 'b) tree -> 'b int |
Leaf and
Node) but not on the values stored inside the nodes.
type int_tree = ILeaf | INode of int_tree * int * int_tree ;; |
tree given above:
type ('a, 'b) int_tree = ILeaf | INode of ('a, 'b) int_tree * 'a int * ('a, 'b) int_tree # 'b ;;
type (+'a:level, #'b:level) int_tree = ILeaf | INode of ('a, 'b) int_tree * 'a int * ('a, 'b) int_tree # 'b ;; |
'a and 'b: the former describes information
attached to the integers stored in the tree while is related to the
structure of the tree. In fact, the type ('a, 'b)int_tree is
isomorphic to ('a int, 'b)tree. This allows distinguishing the
knowledge of the structure of a tree from that of its labels.
To illustrate this point, let us define two functions: size
which calculates the number of nodes of a tree and sum which
calculates the sum of its labels:
let rec size = function ILeaf -> 0 | INode (tl, x, tr) -> size tl + 1 + size tr ;;
val size : ('a, 'b) int_tree -> 'b int
let rec sum = function ILeaf -> 0 | INode (tl, x, tr) -> sum tl + x + sum tr ;;
val sum : ('a, 'a) int_tree -> 'a int |
sum, the security level of the returned integer must be greater
than or equal to the two ones of the tree.
type 'a int_tree1 = ILeaf1 | INode1 of 'a int_tree1 * 'a int * 'a int_tree1 # 'a ;;
type (#'a:level) int_tree1 = ILeaf1 | INode1 of 'a int_tree1 * 'a int * 'a int_tree1 # 'a ;; |
let rec size1 = function ILeaf1 -> 0 | INode1 (tl, x, tr) -> size1 tl + 1 + size1 tr ;;
val size1 : 'a int_tree1 -> 'a int
let rec sum1 = function ILeaf1 -> 0 | INode1 (tl, x, tr) -> sum1 tl + x + sum1 tr ;;
val sum1 : 'a int_tree1 -> 'a int |
size1 gives a less precise description of
the behavior of the function w.r.t. information flow than that of
size: it does not reflect that the size of a tree does not
depend on the value of its labels, as reflected by these computations:
size (INode (ILeaf, x1, ILeaf));;
- : 'a int
size1 (INode1 (ILeaf1, x1, ILeaf1));;
- : !alice int |
type 'a vector = { x: 'a int; y: 'a int } ;;
type (#'a:level) vector = { x: 'a int; y: 'a int } |
vector has one argument which is the common level of the two
integers it is made of. This argument is covariant and guarded. As
for tuples, there is no particular security level attached to the
record structure itself, since it is not really observable in the
language.
let v = { x = x1; y = x2 };;
val v : [> !alice, !bob] vector |
let add_vector v1 v2 = { x = v1.x + v2.x; y = v1.y + v2.y } ;;
val add_vector: 'a vector -> 'a vector -> 'a vector
let rot_vector v = { x = - v.y; y = v.x } ;;
val rot_vector: 'a vector -> 'a vector |
vector with security annotations is
somehow arbitrary. Indeed, it is also possible to distinguish the
information carried by each of its components and hence have two
security levels:
type ('a, 'b) vector2 = { x2: 'a int; y2: 'b int } ;;
type (#'a:level, #'b:level) vector = { x2: 'a int; y2: 'b int } |
let add_vector2 v1 v2 = { x2 = v1.x2 + v2.x2; y2 = v1.y2 + v2.y2 } ;;
val add_vector2: ('a, 'b) vector -> ('a, 'b) vector -> ('a, 'b) vector |
let rot_vector2 v = { x2 = - v.y2; y2 = v.x2 } ;;
val rot_vector2: ('a, 'b) vector2 -> ('b, 'a) vector2 |
rot_vector2
clearly shows that the function performs some permutation of the two
components of the vector.mutable keyword:
type ('a, 'b) mvector = { mutable mx: 'a int; mutable my: 'a int } # 'b ;;
type (='a:level, #'b:level) mvector = { mutable mx : 'a int; mutable my : 'a int; } # 'b |
'a is
invariant, as reflected in the signature by the =.
Secondly, a record involving some mutable field is no longer a simple
tuple: the information it carries is not entirely contained by its
components because its identity (i.e. its address in memory) can be
observed in the language. Hence, its type must carry an additional
security level which tells how much information is attached to the knowledge
of its identity. In our example, this role is played by the argument
'b, which is specified by the clause # 'b at the end of
the definition. To illustrate the use of such a datatype, let us
define the function rot_mvector which rotates in place a vector:
let rot_mvector v = let x = v.mx in v.mx <- v.my; v.my <- x ;;
val rot_mvector : ('a, 'a) mvector -{'a ||}-> unit |
type ('a, 'b) ref = { mutable contents: 'a } # 'b ;;
type (='a:type, #'b:level) ref = { mutable contents: 'a } # 'b |
ref, := and
! on references are regular functions which can be implemented
from the record representation of references:
let ref x = { contents = x } ;;
val ref : 'a -> ('a, _) ref |
let (:=) r x = r.contents <- x ;;
val ( := ) : ('a, 'b) ref -> 'a -{'b ||}-> unit with 'b < level('a) |
let ( ! ) r = r.contents ;;
val ( ! ) : ('a, 'b) ref -> 'c with 'b < level('c) and 'a < 'c |
!alice,
!bob and !charlie, respectively. However, they remained
relatively abstract, because we just declared a series of values to have
these levels---thanks to some type constraint---but we did not
say how a program can really interact with them.!stdin and !stdout, respectively. A
program can interact with them using the usual functions of the
standard library. For instance, print_int outputs an integer on
the standard output:
print_int;;
- : !stdout int -{!stdout ||}-> unit |
!stdout. To print the integer 1, one writes:
print_int 1;;
- : unit |
1 has type 'aint for
every 'a; hence one can instantiate 'a < !stdout and the call
to the function is possible. However, printing the integer x1
(which comes from the principal Alice and hence has the security level
!alice) is not, in the default security policy, legal:
print_int x1;;
This expression generates the following information flow: from !alice to !stdout which is not legal. |
!alice < !stdout. This is not satisfied in the default security
policy which is the empty one: it never allows any
communication from one principal to another. It can be
refined using declarations introduced by the keyword flow:
flow !alice < !stdout;; |
!alice less than
or equal to !stdout. In other words, this allows information
flow from the principal represented by !alice (Alice) to that of
!stdout (the standard output). These declarations are naturally
``transitive''. For instance, if one declares:
flow !bob < !alice;; |
print_int x2;;
- : unit |
!stdin intends to represent the
standard input in the type system. For instance, the function
read_line has the following type:
read_line;;
- : unit -{[< !stdout, !stdin] | End_of_file: !stdin |}-> !stdin string |
read_line
``flushes standard output, then reads characters from standard
input until a newline character is encountered [and] returns the
string of all characters read, without the newline character at the
end''. Thus, invoking read_line affects both the standard
input and output, which explains the first annotation in the arrow of
its type. Furthermore, if the user sent the ``end-of-file'' sequence
(e.g. by typing ^D), the function raises the exception
End_of_file, hence the second annotation on the arrow. Lastly,
a string obtained by reading on the standard input must have the level
!stdin:
let s1 = read_line ();;
val s1 : !stdin string Current evaluation context has level !stdin |
flow !stdin < !stdout;; |
echo
which ``pipes'' the standard input to the standard output:
let echo () = try while true do let s = read_line () in print_string s done with End_of_file -> ();;
val echo : unit -{[< !stdout, !stdin] ||}-> unit |
struct ...end construct, and is usually given a name with the
module binding. For instance, one may define a structure
implementing sets of integers (with binary trees):
module IntSet = struct type 'a t = Empty | Node of 'a t * 'a int * 'a t # 'a let empty = Empty let rec add x = function Empty -> Node (Empty, x, Empty) | Node (l, y, r) -> if x < y then Node (add x l, y, r) else Node (l, y, add x r) let rec mem x = function Empty -> false | Node (l, y, r) -> (x = y) || mem x (if x < y then l else r) end;;
module IntSet : sig type (#'a:level) t = Empty | Node of 'a t * 'a int * 'a t # 'a val empty : 'a t val add : 'a int -> 'a t -> 'a t val mem : 'a int -> 'a t -> 'a bool end |
t), and three values: the empty set,
empty, and two functions operating on sets, add (to add an
integer to a set) and mem (to test whether an integer belongs to a
set). The system outputs the signature of the structure, which
is a list of its components with their declaration. Outside the
structure, its components can be referred to using the ``dot
notation'', that is, identifiers qualified by a structure name. For
instance, IntSet.add refers to the function add of this
structure.
IntSet.add x1 (IntSet.add x2 IntSet.empty);;
- : [> !alice, !bob] IntSet.t |
module type INTSET = sig type (#'a:level) t val empty: 'a t val add: 'a int -> 'a t -> 'a t val mem: 'a int -> 'a t -> 'a bool end;;
module AbstractIntSet = (IntSet : INTSET);;
module AbstractIntSet : INTSET |
compare defining a total order between them:
module type ORDERED_TYPE = sig type (#'a:level) t val compare : 'a t -> 'a t -> 'a int end;; |
compare xy is expected to return 0 if
x is equal to y, a negative integer if x is less
than y and a positive integer otherwise.) In this signature,
the type of the elements, t, is parameterized by one security
level which describes all the information leaked by a comparison
(as reflected by the type of compare). However, this does not
prevent to instantiate it with more complex data types, which are
originally parameterized by several security levels:
module IntList : ORDERED_TYPE = struct type 'a t = ('a int, 'a) list let rec compare l1 l2 = match l1, l2 with [], [] -> 0 | [], _ :: _ -> -1 | _ :: _, [] -> 1 | hd1 :: tl1, hd2 :: tl2 -> let c = Pervasives.compare hd1 hd2 in if c = 0 then compare tl1 tl2 else c end;;
module IntList : sig type (#'a:level) t val compare : 'a t -> 'a t -> 'a int end |
Elt as argument which must have the
signature ORDERED_TYPE:
module Set (Elt: ORDERED_TYPE) = struct type 'a element = 'a Elt.t type 'a t = Empty | Node of 'a t * 'a element * 'a t # 'a let empty = Empty let rec add x = function Empty -> Node (Empty, x, Empty) | Node (l, y, r) -> if Elt.compare x y < 0 then Node (add x l, y, r) else Node (l, y, add x r) let rec mem x = function Empty -> false | Node (l, y, r) -> let c = Elt.compare x y in (c = 0) || mem x (if c < 0 then l else r) end;;
module Set : functor (Elt : ORDERED_TYPE) -> sig type (#'a:level) element = 'a Elt.t type (#'a:level) t = Empty | Node of 'a t * 'a Elt.t * 'a t # 'a val empty : 'a t val add : 'a Elt.t -> 'a t -> 'a t val mem : 'a Elt.t -> 'a t -> 'a bool end |
IntSet example, it would be good style to hide the
actual implementation of the type of sets. This can be achieved by
restricting Set by a suitable functor signature. Firstly, let
us define the type of a module implementing a set structure:
module type SET = sig type (#'a:level) element type (#'a:level) t val empty: 'a t val add: 'a element -> 'a t -> 'a t val mem: 'a element -> 'a t -> 'a bool end;; |
Set functor takes
a structure of signature ORDERED_TYPE and returns one of
signature SET, so it may be declared with the following type:
module Set (Elt: ORDERED_TYPE) : (SET with type 'a element = 'a Elt.t) = struct ... end |
with type 'a element = 'a Elt.t
has the same purpose as in Objective Caml: it points out the fact that
the sets contain elements of type Elt.t, i.e. that the
functions add and mem can be applied with arguments of
this type. To conclude with this example, one can retrieve our first
implementation of integer sets, the module IntSet, as an
instance of the functor Set:
module IntSet' = Set (struct type 'a t = 'a int let compare = Pervasives.compare end);;
module IntSet' : sig type 'a element = 'a int type 'a t val empty : 'a t val add : 'a element -> 'a t -> 'a t val mem : 'a element -> 'a t -> 'a bool end |
module type IN = sig level Data level Prompt val read : unit -{[< Prompt] ||}-> Data string end;; |
Data is the
security level of data read on the input channel; and Prompt
represents the information leaked on the channel when one starts
listening on it. At the time being, nothing is known about these
levels, so they remain ``abstract''. The function read is
intended to read one line on the underlying channel. It naturally produces a
string whose level is Data (let us remark that, in this model,
reading can never fail). An implementation of this signature using
the standard input would be as follows:
module Stdin = struct level Data = !stdin level Prompt less than !stdin, !stdout let read () = try read_line () with End_of_file -> `` end;;
module Stdin : sig level Data = !stdin level Prompt less than !stdout, !stdin val read : unit -{[< !stdout, !stdin] ||}-> !stdin string end |
!stdin,
so Data is declared to equal to it in Stdin. Invoking
read_line affects the standard input and the standard output
(because it is flushed), so Prompt must be less than or equal to
!stdin and !stdout. Then, the module Stdin
implements the signature IN, which may be immediately verified by
a type constraint:
module AbstractStdin = (Stdin : IN);;
module AbstractStdin : IN |
module type OUT = sig level Data val print : Data string -{Data ||}-> unit end;; |
Data
which represents the information which may be sent on the channel.
(We do not consider the possibility of receiving information
from an output channel, for instance because of a buffer overflow.) The
module Stdout implements this signature for the standard output:
module Stdout = struct level Data = !stdout let print = print_endline end;;
module Stdout : sig level Data = !stdout val print : !stdout string -{!stdout ||}-> unit end;; |
copy whose purpose is simply to read one line on the input
channel and print it on the output channel. However, it is not enough
to require the two structures parameterizing the functor to have the
respective signature INPUT and OUTPUT: indeed, the
function copy implemented by the functor generates an
information flow from the channel represented by the former to that of
the latter. Hence the security level Data of the input channel,
must be declared to be less than or equal to that of the output
channel.
module Copier (I : IN) (O : OUT with level Data greater than I.Data) = struct let copy () = O.print (I.read ()) end;;
module Copier : functor (I : IN) -> functor (O : sig level Data greater than I.Data val print : Data string -{Data ||}-> unit end) -> sig val copy : unit -{[< O.Data, I.Prompt] ||}-> unit end |
withlevel appearing in
the type of the second argument of the function. Its semantics is
similar to that of withtype or withmodule in Objective
Caml: it refines the definition of the level Data in the
signature of the module O. The clause greater than I.Data
declares that this security level must be that of a principal allowed to
``receive'' information from the channel implemented by the
structure I whose level is I.Data.
module Copier' (O : OUT) (I : IN with level Data less than O.Data) = struct let copy () = O.print (I.read ()) end;;
module Copier' : functor (O : OUT) -> functor (I : sig level Data less than O.Data level Prompt val read : unit -{Prompt ||}-> Data string end) -> sig val copy : unit -{[< I.Prompt, O.Data] ||}-> unit end |
source in I must be allowed to send information
to O.Data.Copier dedicated to the standard input and output. This
requires to allow information flow from the former to the latter,
which can be done by the toplevel declaration:
flow !stdin < !stdout;; |
Stdin.Data is less than or
equal to Stdout.Data, so Stdin and Stdout are
legal arguments for Copier:
module StdCopier = Copier (Stdin) (Stdout);;
module StdCopier : sig val copy : unit -{[< Stdout.Data, Stdin.Prompt] ||}-> unit end |
let definitions and their evaluation may have
side-effects or raise exceptions. It is worth noting that an
exception which escapes the scope of a top-level let definition
cannot be trapped further, so it terminates the program.let definition but also two lists of security levels, or
bounds written from ... to... where each ... stands for
a list of security levels. The lower bound (appearing after
the from keyword) describes the side-effects performed by the
evaluation of the definition, roughly speaking it includes the
security level(s) of data structures the definition
may affect. The upper bound (appearing after the to
keyword) tells how much information is attached to the exceptions
the definition may raise. This process is generalized to the
whole module language by associating to every definition and module
expression a pair of bounds. Because they have no computational
content, the bounds of external, type, level,
exception, moduletype, open and include
definitions are always empty. The bounds of a module definition
are obtained by considering recursively the module expression which
appears in the right-hand-side. struct def1 ... defnend
consists in evaluating successively each of the definitions, then the
bounds associated to the whole module expression are naturally
obtained by merging those of the definitions def1 to
defn. Moreover, while considering this sequence of
definitions, defi is evaluated if and only if none of
def1 to defi-1 raised an exception. As a result,
to prevent any illegal information flow, the upper bounds of the
former must be less than or equal to the lower bound of the latter.
module type S = sig val x : 'a int end;; module F (X: S) = struct let _ = r1 := X.x; if X.x = x2 then raise Exit end;;
module F : functor (X : S) -{!alice | !bob}-> sig end |
F may
generate a side-effect on cells of level !alice and may raise an
exception at level !bob. Then, an application of F
inserts !bob in the evaluation context's security level:
module F0 = F (struct let x = 1 end);;
Current evaluation context has level !bob |
F if the
evaluation context's security level is less than or equal to
!alice, which is no longer the case after a first application of
F:
module F1 = F (struct let x = 1 end);;
This expression is executed in a context of level !bob but has an effect at level !alice. This yields the following information flow: from !bob to !alice which is not legal. |
flowcamlc allows to type-check them, and also
translates them into regular Objective Caml source code files, so that
they can be compiled using the compilers ocamlc or
ocamlopt, yielding a standard executable./etc/passwd
registers the list of logins, with, for each of them, a password and
some administrative information such as a numeric id, the user's home
directory and shell. Besides, the file /etc/shadow associates
to every login a password stored in a encrypted form (with some optional
aging information), which is used in place of that in
/etc/passwd. Our program aims at synchronizing these two files,
i.e. generating an entry in /etc/shadow for every account
which is listed only in /etc/passwd. In the forthcoming
subsections, we will explain step by step how the source code is
organized, how it is verified and compiled thanks to the Flow Caml
system. The type system will allow us to check that running the
program cannot reveal to the user which invokes the command any
information about the passwords stored in the two files.A comprises one or two files,
among:
.fml, which contains a
sequence of definitions, analogous to the inside of a
struct...end construct;
.fmli, which contains a
sequence of specifications, analogous to the inside of a
sig...end construct.
flow declaration and optional affects and raises
statements, whose
respective purposes will be explained in the
sections 2.8.2
and 2.8.3.) Both files define a structure
named A (same name as the base name of the two files, with the
first letter capitalized), as if the following definition was entered
at top-level:
module A : sig (* specifications of file a.fmli *) end = struct (* definitions of file a.fml *) end;; |
flowcamlc, following for each unit A one of the
three above schemes:
A defined in files
a.fmli and a.fml is described in
figure 2.1. First, the Flow Caml
interface a.fmli is fed to flowcamlc, which
checks its well-formedness and produces a compiled version of it,
a.fcmi. It also translates the interface file
into a regular Objective Caml one, namely a.mli.
Second, the implementation a.fml can be type-checked by
flowcamlc. The compiler computes the most general interface
for the implementation, and checks it fulfills the declared one
(i.e. that stored in a.fcmi). Furthermore, the source
code of the unit in a.fml is translated into a Objective
Caml implementation file, a.ml. Then, a.mli
and a.ml can be compiled with ocamlc to produce a
compiled interface a.cmi and a bytecode object file
a.cmo.
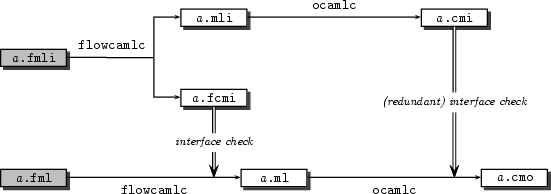
Figure 2.1: Compilation scheme of a unit defined in a.fmli and a.fml
A by providing only an implementation file a.fml
but no interface file. This yields the compilation scheme of
figure 2.2: the implementation
a.fml can be directly passed through flowcamlc
and the interface computed by type inference is stored itself in
a.fcmi.

Figure 2.2: Compilation scheme of a unit defined in a.fml
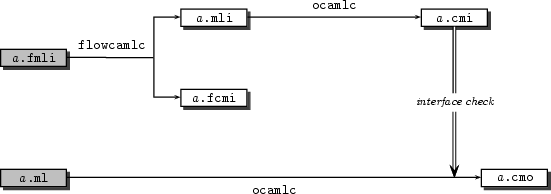
Figure 2.3: Compilation scheme of a unit defined in a.fmli and a.ml
Passwd
and Shadow are low-level modules which implement functions for
accessing the /etc/passwd and /etc/shadows files:
their implementations are directly written in Objective Caml (files
passwd.ml and shadow.ml), and only interfaces are
provided in Flow Caml (files passwd.fmli and
shadow.fmli). These interfaces assign security levels to the
information manipulated by the units: data stored in
/etc/passwd has the level !passwd_file, except the
passwords, which have level !password. Similarly,
information from /etc/shadow receives the level !shadow_file
and !shadow_password. The unit Verbose provides a verbose
mode: if the user runs the program with the -v option, then the
execution is traced on the standard output. The body of the
program is in Main. These last two units are fully implemented
in Flow Caml: implementation (verbose.fml and
main.fml) and interface (verbose.fmli and
main.fmli) files are provided for each of them.flow declarations allow specifying the security policy by
setting inequalities between principals. We have seen that the
toplevel system allows the programmer to refine the security policy
incrementally, by entering new flow declarations which remain
valid until the end of the interactive session.flowcamlc, every
compilation unit must come with its own security policy, i.e. a
flow declaration which specifies sufficient assumptions on
principals for its source code to be well-typed. This declaration
must be provided at the beginning of the implementation and interface
files. For instance, the compilation unit Verbose of our example
begins with the following declaration:
flow !arg < !stderr, !stdout |
!stderr and !stdout
represent the standard error and the standard output of the program,
respectively. !arg is the security level of the command-line
arguments. The declaration is a shorthand for
flow !arg < !stderr and !arg < !stdout |
!arg < !stdout
and !arg < !stderr. When a compilation unit includes
no flow declaration---as Passwd and Shadow in the
example---this simply means it is well-typed in every security
policy.flow
declaration in every compilation unit of a program is of main
importance for modularity of programming and re-usability of code, in
the context of separate compilation. Indeed, this allows for instance
having libraries (such as the standard one) used in programs which
have different security policies. Otherwise, one would have to
write or compile a specialized version of these libraries for each
program which expects a different policy.flowcamlpol, to compute
the (minimal) security policy under which a program is (checked to be)
safe. The usage of flowcamlpol is---to some extent---similar
to that of a linker of object files: it expects as argument the
name of the compiled interfaces of the program's units, in the same
order as the corresponding object files will be linked. For our
example, one must run the command:
flowcamlpol passwd.fcmi shadow.fcmi debug.fcmi main.fcmi |
|
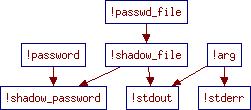 |
-graph option. It shows some interesting properties of the
information flow graph of the program, which have been established
automatically by the type system. For instance, the
standard output is not related to sensitive data stored in the
/etc/passwd and /etc/shadow files, i.e. the user
passwords.
print_string Sys.argv.(0);; |
!arg < !stdout is
enforced. However, the existence of a ``minimal'' solution to this
problem is no longer ensured when considering the module language.
Indeed, typing module expressions requires comparing type
schemes, i.e. verifying that a given scheme is an instance of another
one, which cannot yield principal flow declarations. For
instance, the comparison of [< !alice, !bob]int with
!charlieint requires the least upper bound of the levels
!alice and !bob to be less than or equal to
!charlie, which is not expressible in a flow statement.
ocamlc -o passwd2shadow passwd.cmo shadow.cmo verbose.cmo main.cmo |
passwd2shadow, the
definitions of Passwd, Shadow, Verbose and
Main are successively evaluated, until an uncaught exception is
raised or the end is reached. Then, when gaining control, each unit
acquires the information that the previous ones normally terminated.
So, in order to trace this possible information flow, one has to
consider the bounds of the underlying structures, as if the
program where defined in a single unit such as:
module Passwd = struct ... end module Shadow = struct ... end module Verbose = struct ... end module Main = struct ... end |
affects
and raises statements, respectively , which appears
between the flow declaration and the signature (as usual,
omitted bounds are supposed to be empty). For instance, the interface
of Verbose declares the following bounds
affects !arg raises !arg |
Verbose has side-effect of level
!arg and can raise an exception at this level. This
statement appears only in the interface: when type-checking the
implementation, the bounds are inferred from the source code and
compared to those provided in the interface. Unit1,
..., Unitn to produce an executable, one has to check
that, for every i, the upper bounds of Unit1 to
Uniti-1 are less than or equal to the lower bound of
Uniti, which is in fact achieved by the flowcamlpol
command, at the same time it computes the security policy:
flowcamlpol passwd.fcmi shadow.fcmi debug.fcmi main.fcmi |


