This mathematical gallery contains different random geometric objects that appear in my research. To get a vectorial image, click on the image.
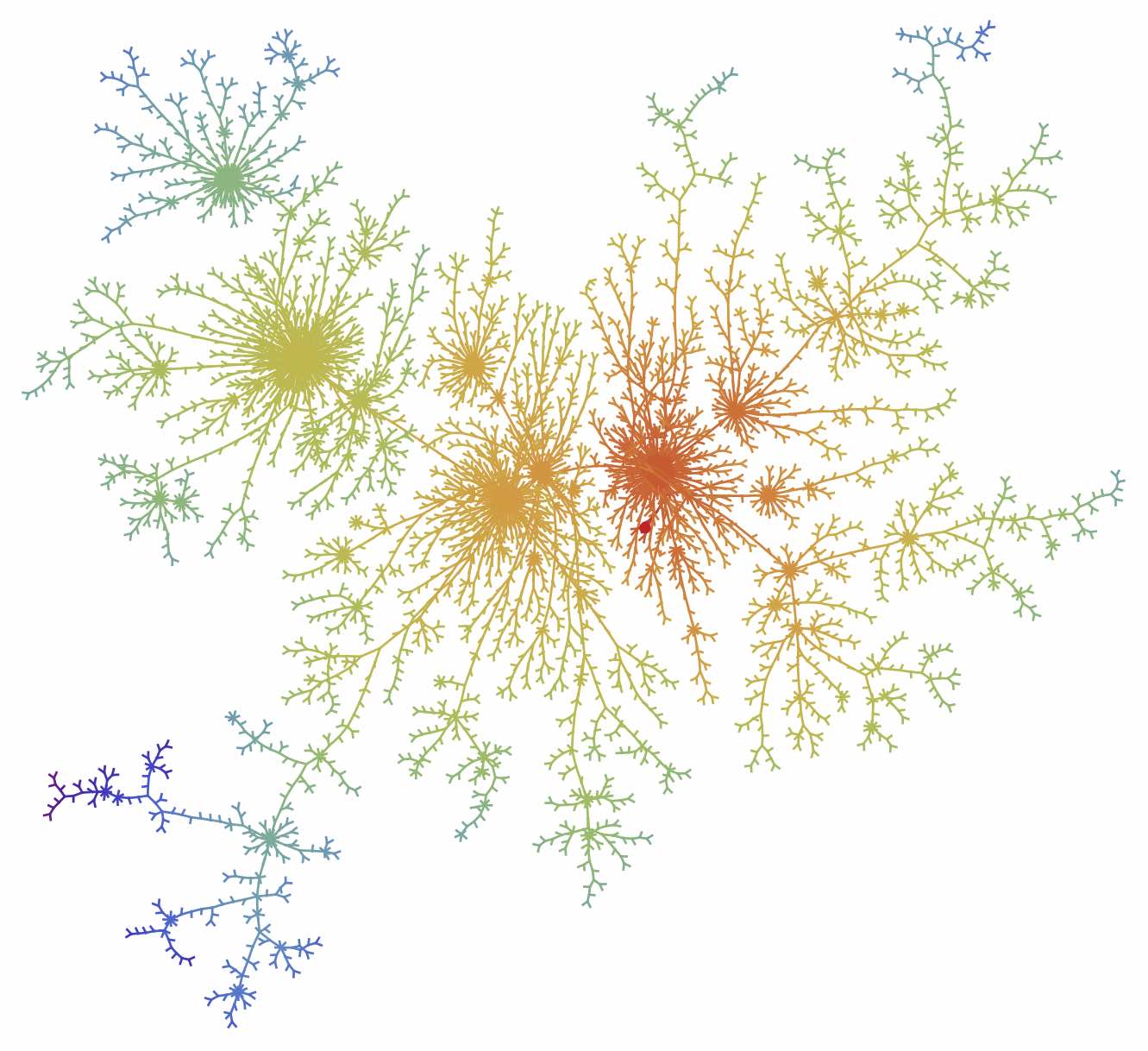
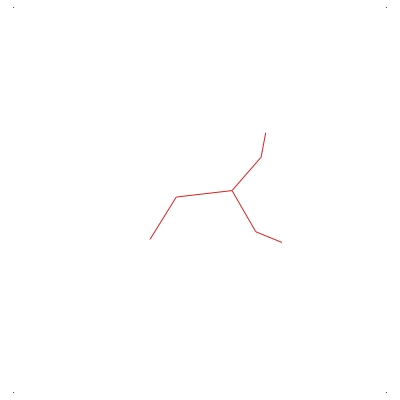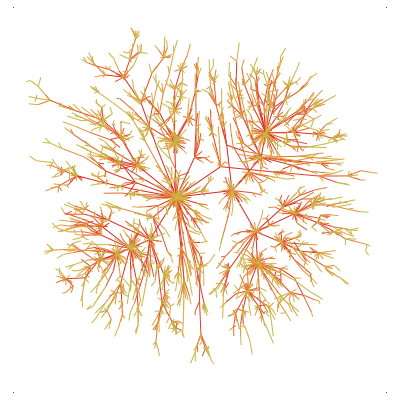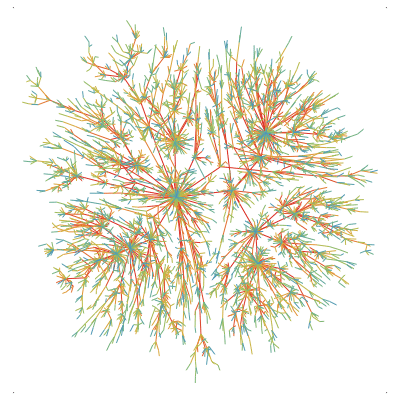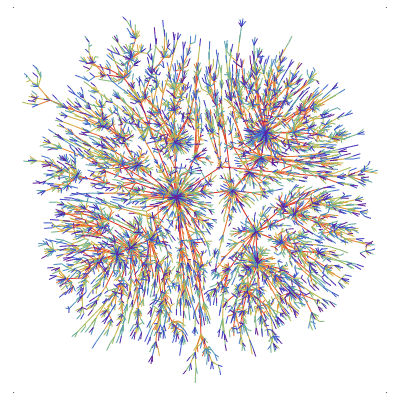
Random trees
These are simulations of (approximations of) stable Lévy trees. More precisely, they are random Bienaymé--Galton-Watson trees, conditioned on having a large fixed number of vertices, with a critical offpsring distribution that falls in the domain of attraction of a stable law (from top to bottom and from left to right the indices are 1.1, 1.5, 1.9 and 2). The last tree (corresponding to the index 2), is an approximation of Aldous' Brownian Continuum Random Tree.
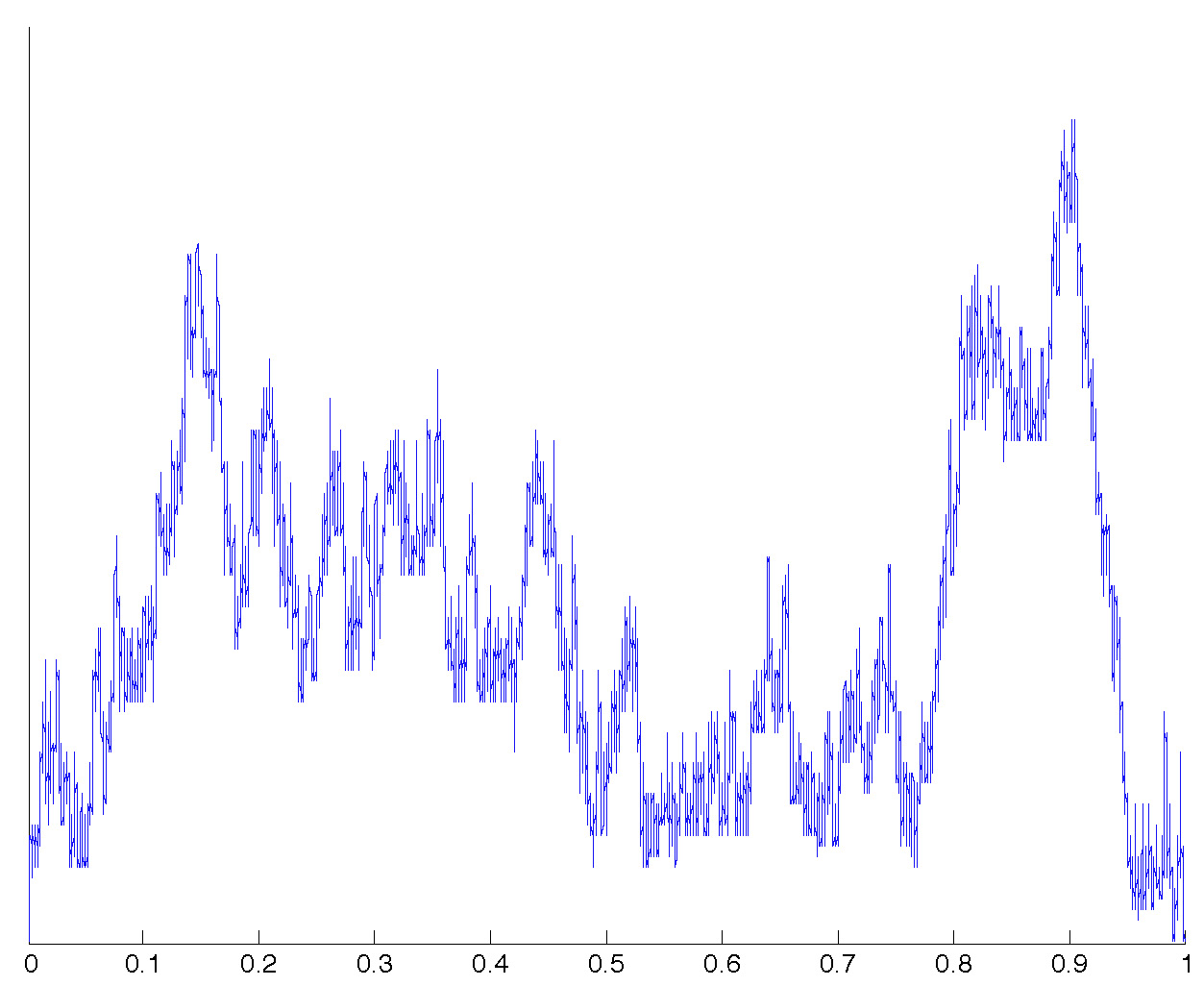
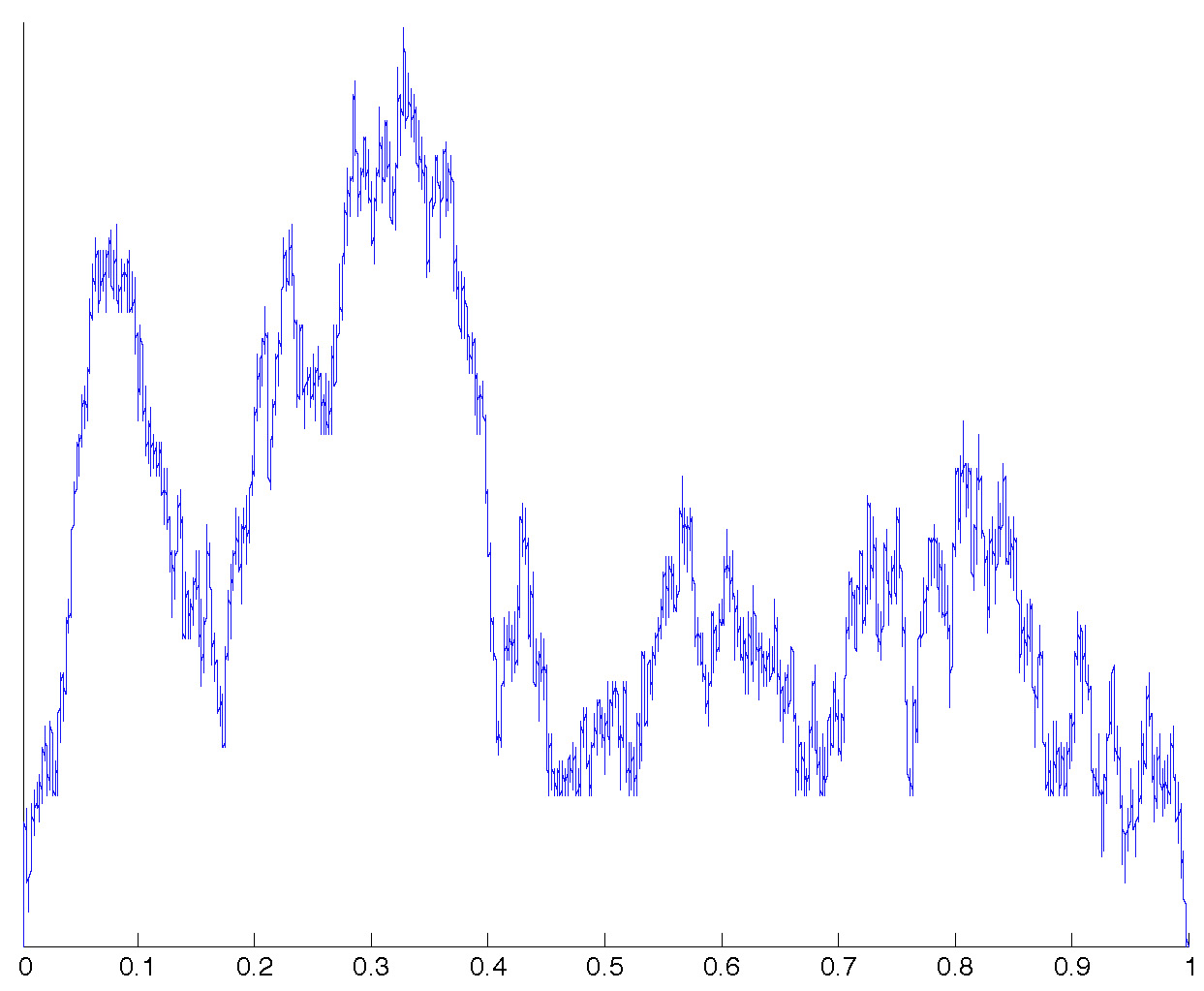
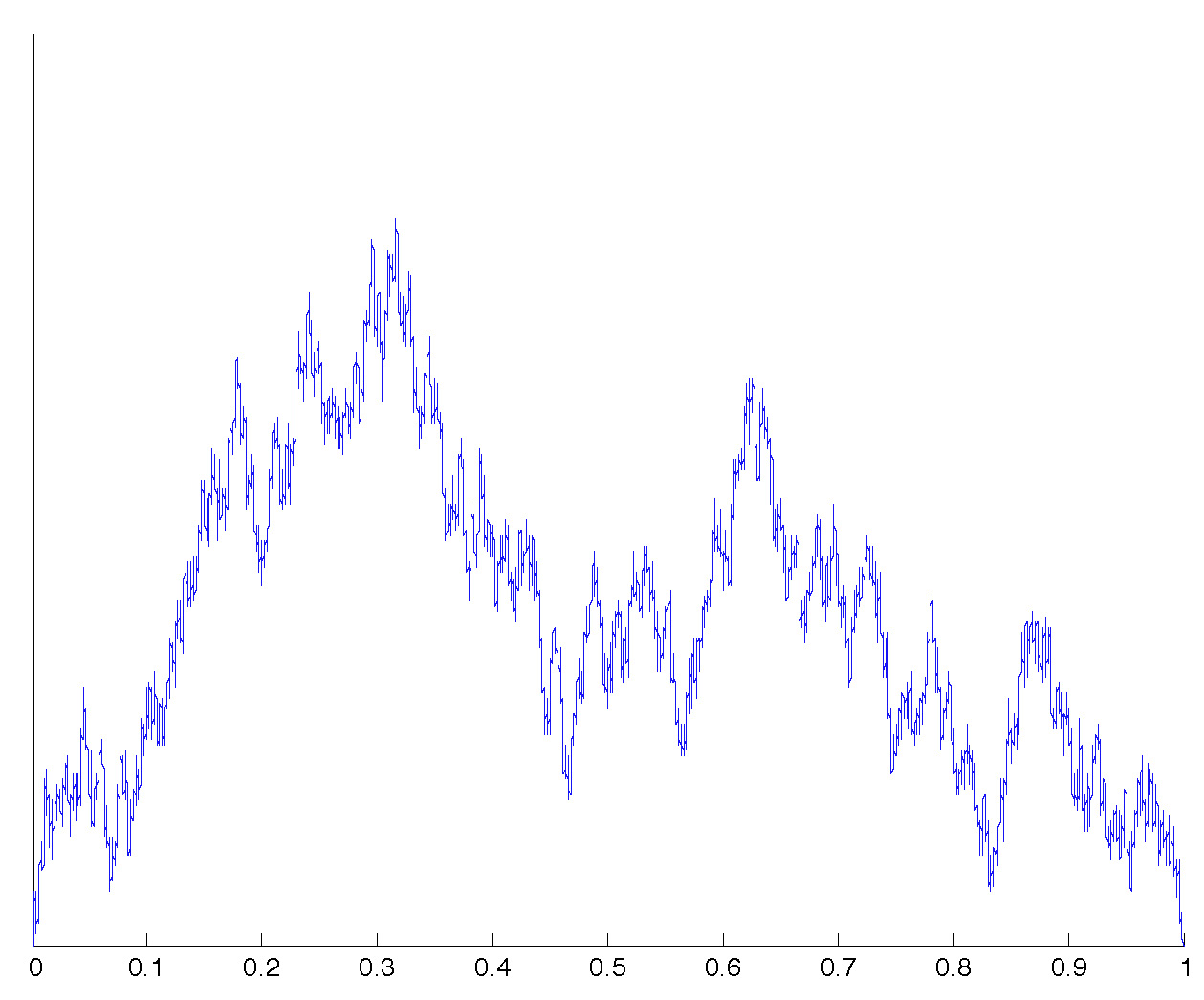
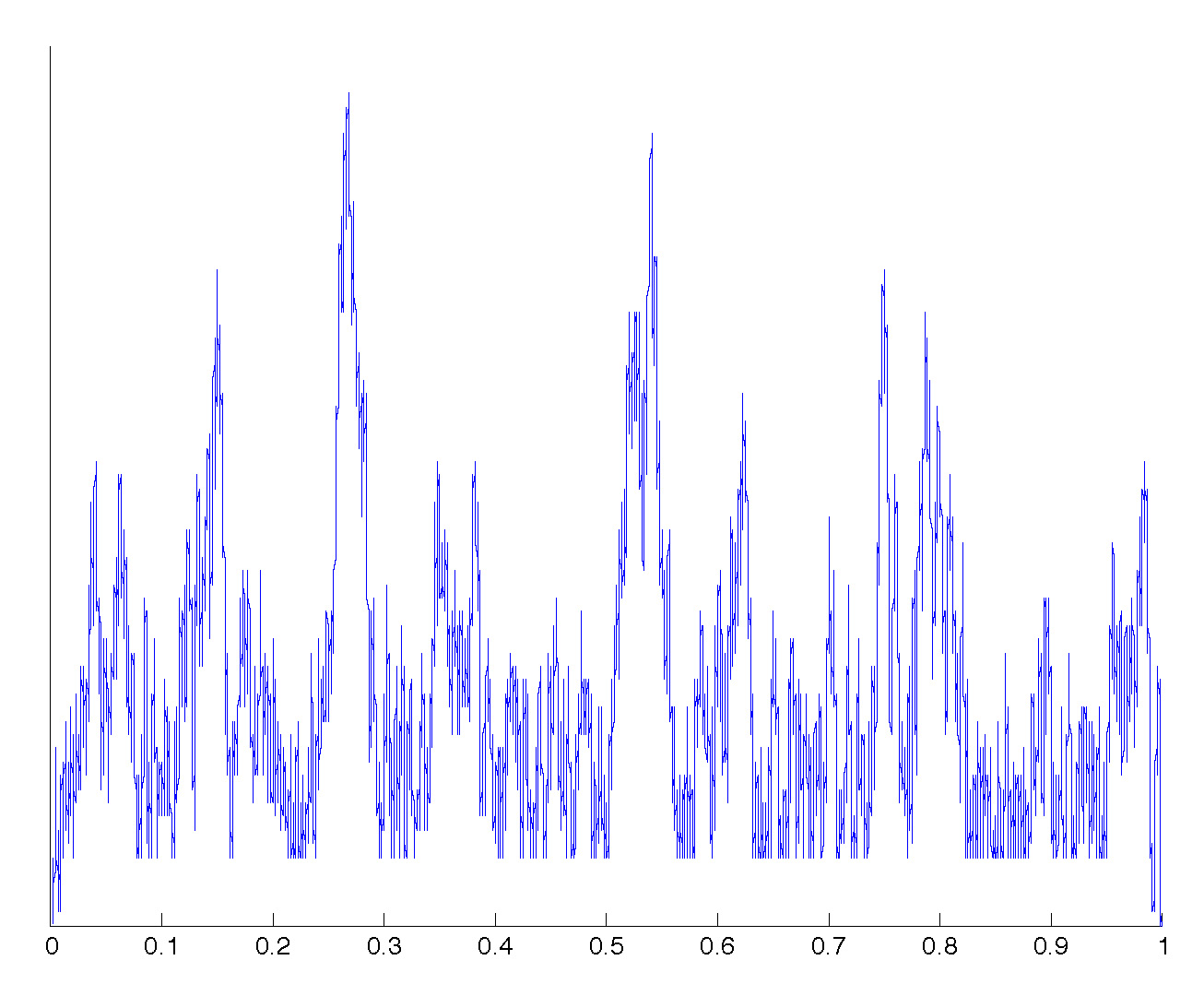
The previous trees are coded by excursion-type continuous functions:
These represent approximations of the normalized excursions of the so-called height process (introduced by Le Gall and Le Jan) of indices 1.1, 1.6 and 2 (the latter being the Brownian excursion). They are, roughly speaking, normalized contour functions of the previous trees.
Some other pictures (with indices equal to 1.1, 1.5 and 2) where colors represent the distance from the root:
A more unusual large Bienaymé-Galton-Watson tree, paired with its normalized contour function:
Here, the offspring distribution is sub-critical and has a heavy tail, which gives rise to a condensation phenomenon (the tree has a unique vertex with macroscopical degree, comparable to the size of the tree). See this article for details.
Random laminations
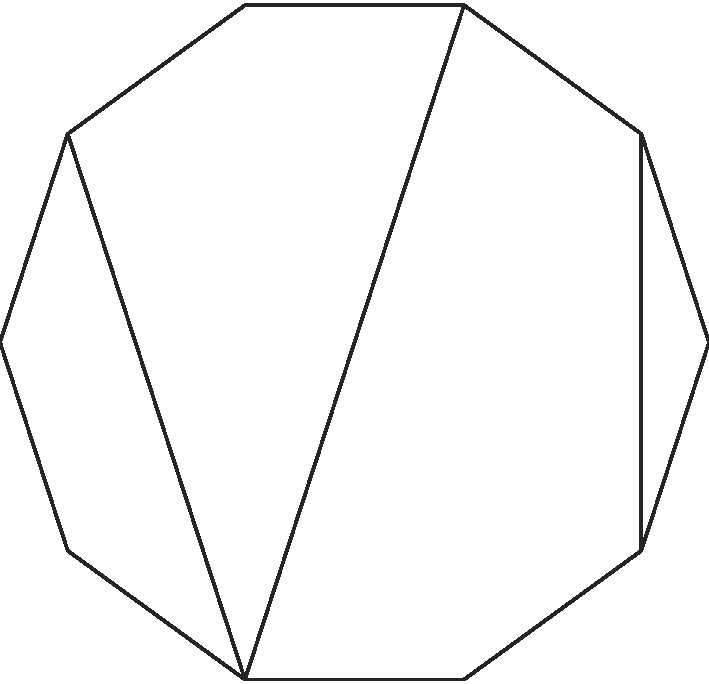
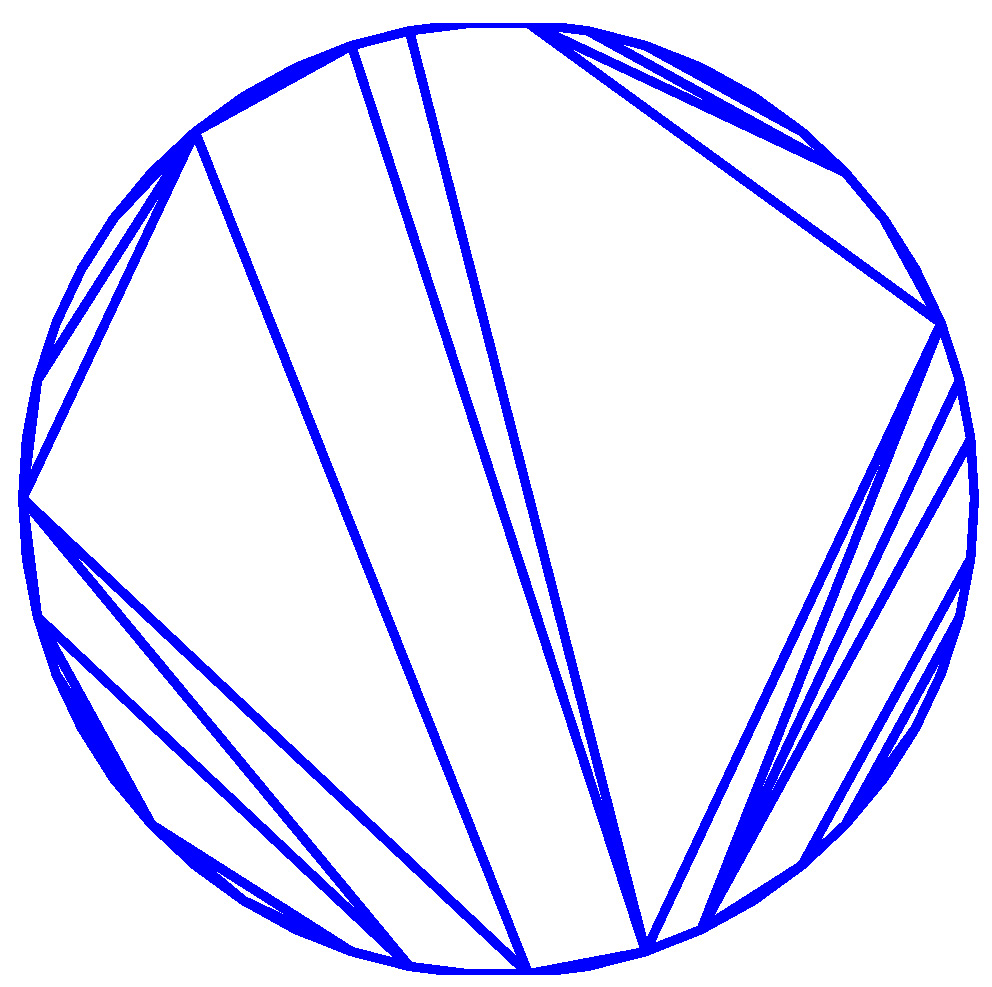
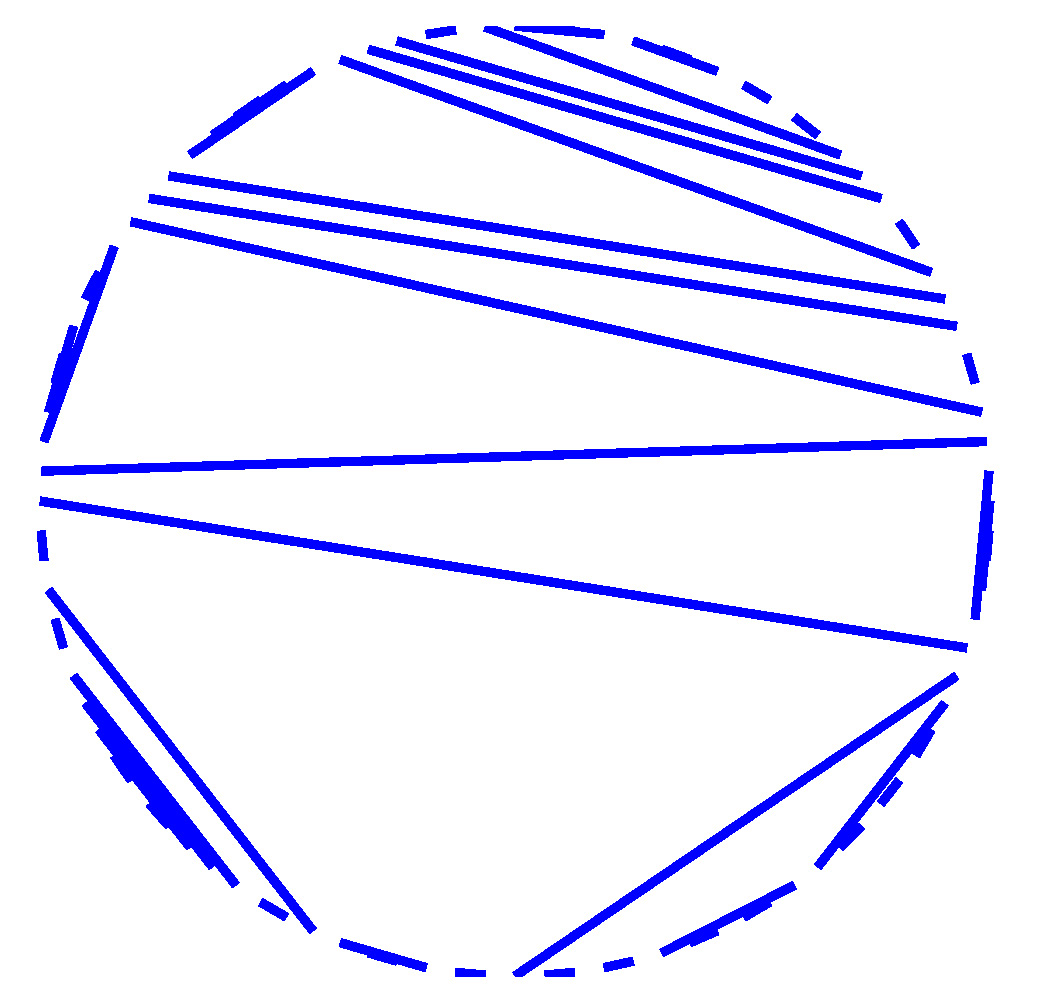
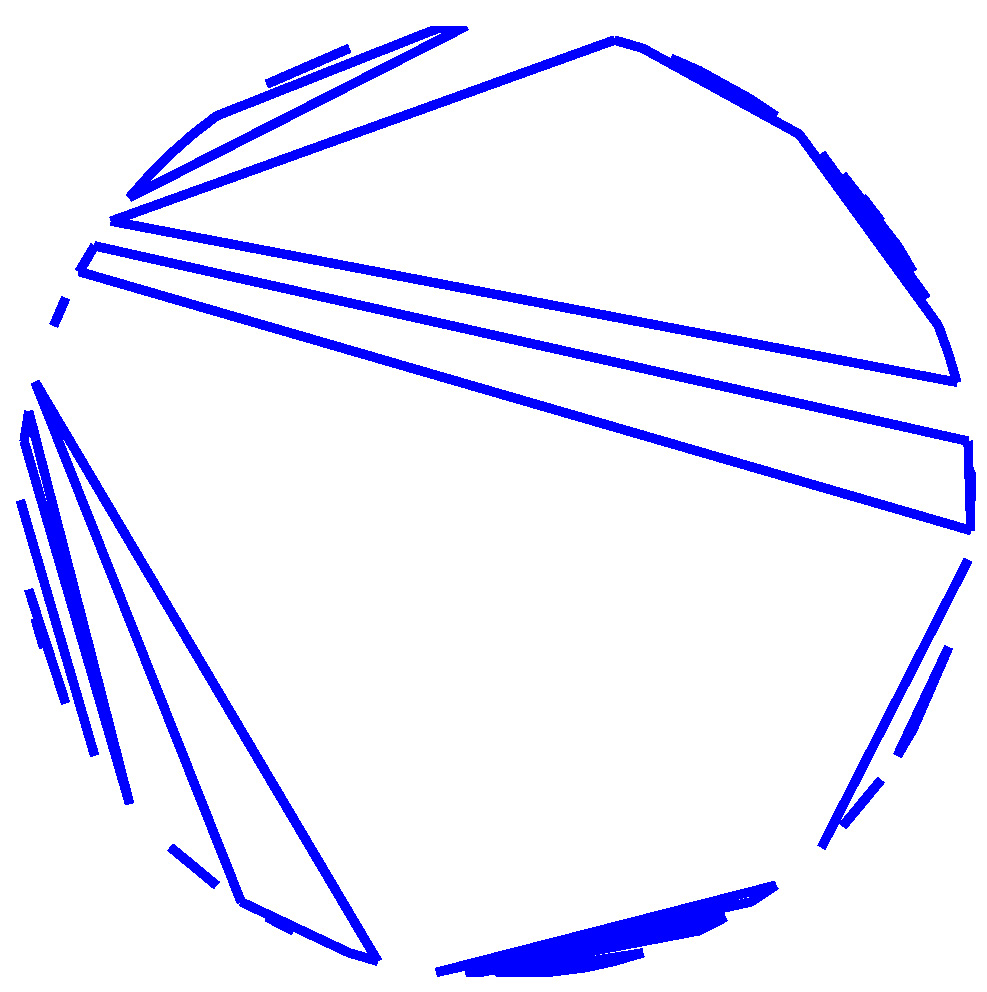
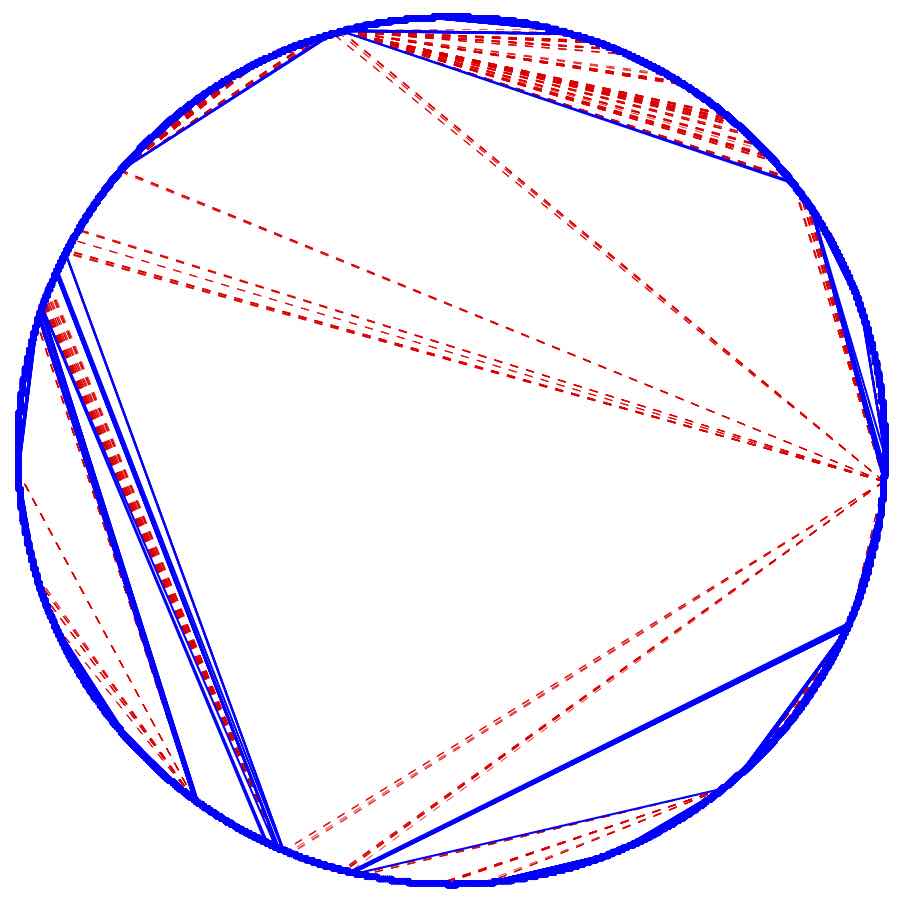
Roughly speaking, laminations are continuous analogs of dissections. A dissection of a convex polygon is a collection of non-crossing diagonals; for example:
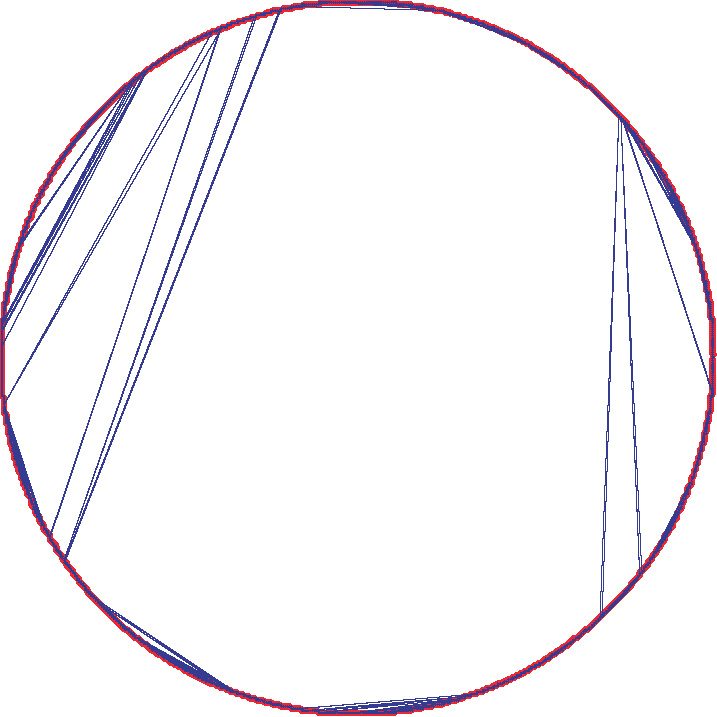
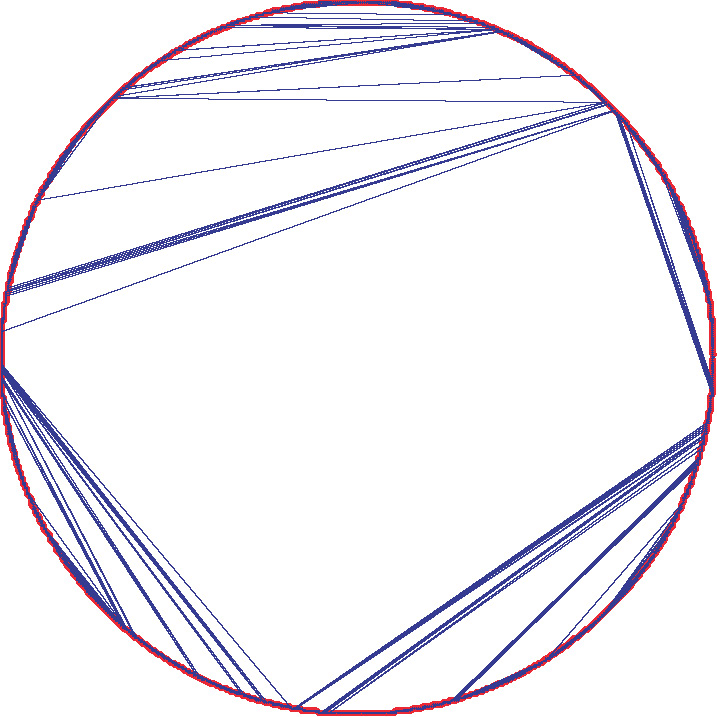
When the number of vertices of a regular polygon tends to infinity and when dissections are chosen at random according to a Boltzmann-type distribution with weights belonging to the domain of attraction of a stable law, large faces appear:
The index is respectively equal to 1.1, 1.5, 1.9 and 2. When the index is 2, we get a random continuous triangulation of the disk, called Aldous' Brownian triangulation. See this article for details. topRandom non-crossing configurations
A non-crossing configuration of a regular polygon is by definition a non-crossing collection of sides and diagonals (in particular, a dissection is a non-crossing configuration). Here are examples of random non-crossing configurations, chosen uniformly at random among a certain class (the polygon has either 50, or 100 vertices):
These are respectively a dissection, a non-crossing tree, a non-crossing pair-partition and a non-crossing partitition, chosen uniformly at random. When the number of vertices of the polygon tends to infinity, triangular faces seem to appear. Actually, all these models converge to the same limiting object (the Brownian triangulations), so that in a certain sense these models become the same in the limit. For more details concerning this intriguing universality phenomenon, see this article.
Instead of choosing these objects uniformly at random, it is possible to choose them according to Boltzmann weights belonging to the domain of attraction of a stable law. In the case of non-crossing partitions, the limiting objects are the stable laminations (and there is a nice connection with non-commutative probability), see this article. In the case of non-crossing trees, a new limiting object appears, which is roughly speaking obtained from stable laminations by triangulated all the faces uniformly at random, see this article:
Random looptrees
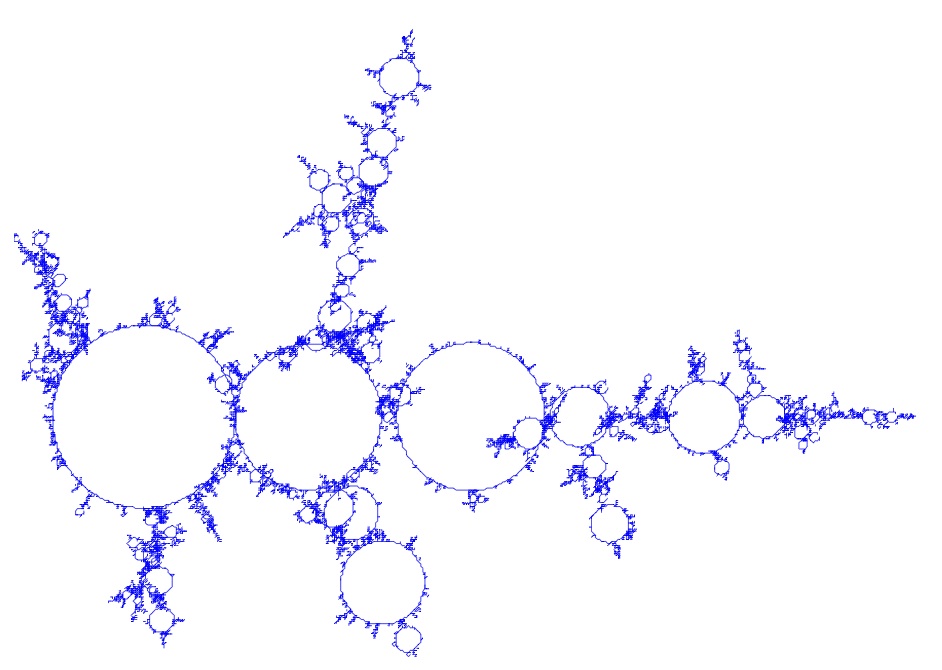
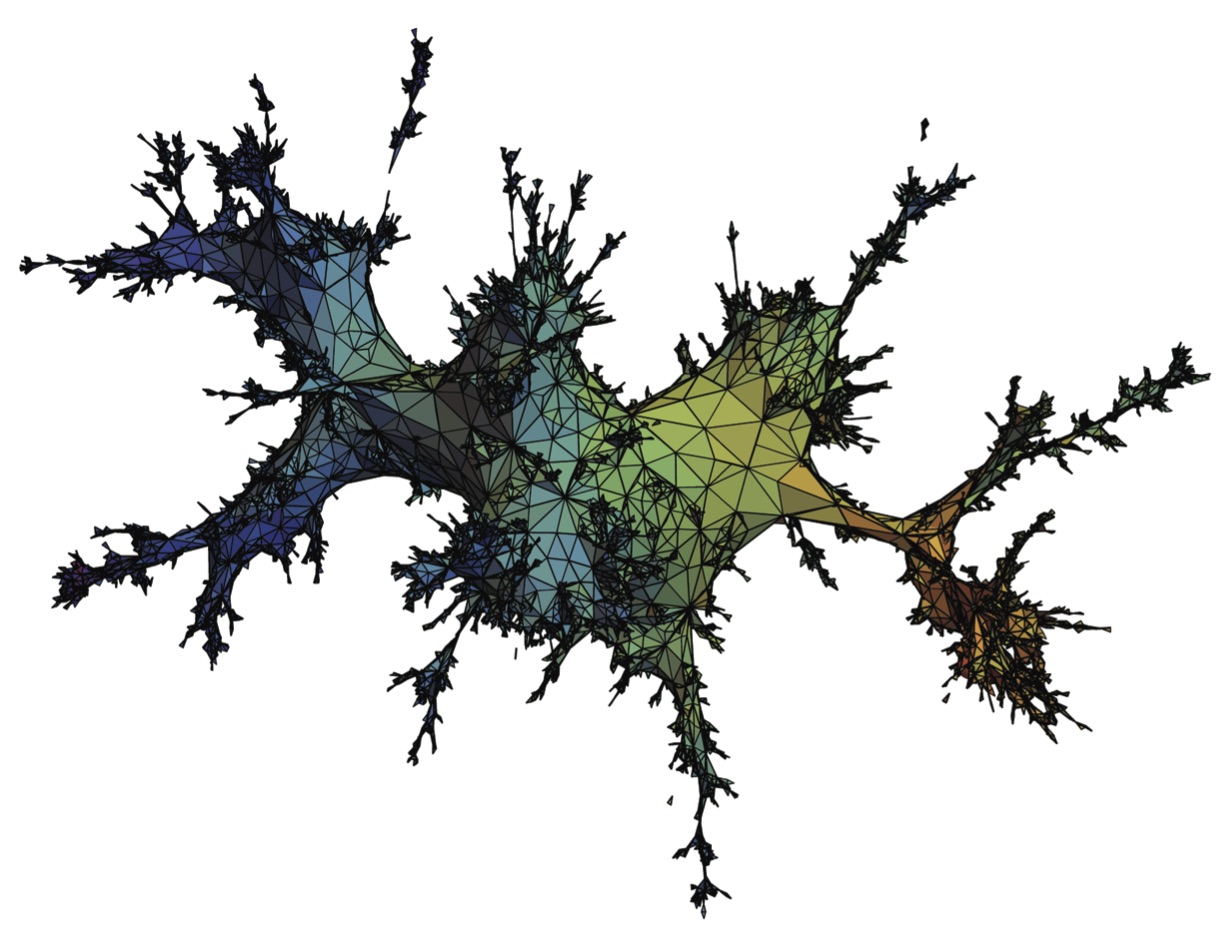
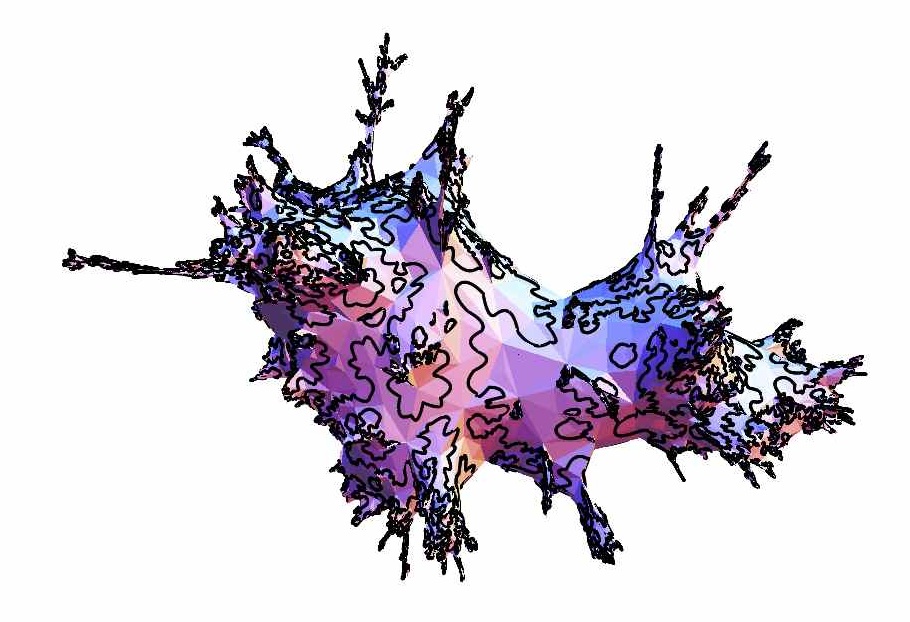
We saw that dissections chosen at random according to Boltzmann weights belonging to the domain of attraction of a stable law, seen as compact subsets of the disk, converge to a sable lamination. Something interesting happens when one now views dissections as compact metric spaces (the vertices of a dissection are equipped with the graph distance, where each edge has unit length). In this case, when alpha is the index of stability, these dissections, appropriately rescaled, converge to a random limiting compact metric space called the alpha-stable looptree. Here is a planar embedding (but neither isometric, nor proper) of a realization of 1.07-stable looptree:
One also shows that the alpha-stable looptree is the scaling limit of discrete looptrees associated with critical Bienaymé-Galton-Watson trees with critical offspring distribution belonging to the domain of attraction of a stable law:
For more details, see this article.
However, when the Boltzmann weights is not heavy-tailed any more (this includes the model of uniform dissections and of uniform p-angulations), the loops degenerate and the limit is now a multiple of the Brownian tree (the dependence of the multiplicative constant in the weights is rather intruiguing), see this article. Here is an example a large uniform dissection:
Preferential attachment
We are interested in the model of trees built by preferential attachment: starting with an initial tree S (called the seed), at each step an existing vertex is chosen at random proportionally to its degree, and a new vertes is attached to it. On the left, an animation of a tree built by preferential attachement and on the right a tree built by uniform attachment (one chooses an existing vertex uniformly at random instead):
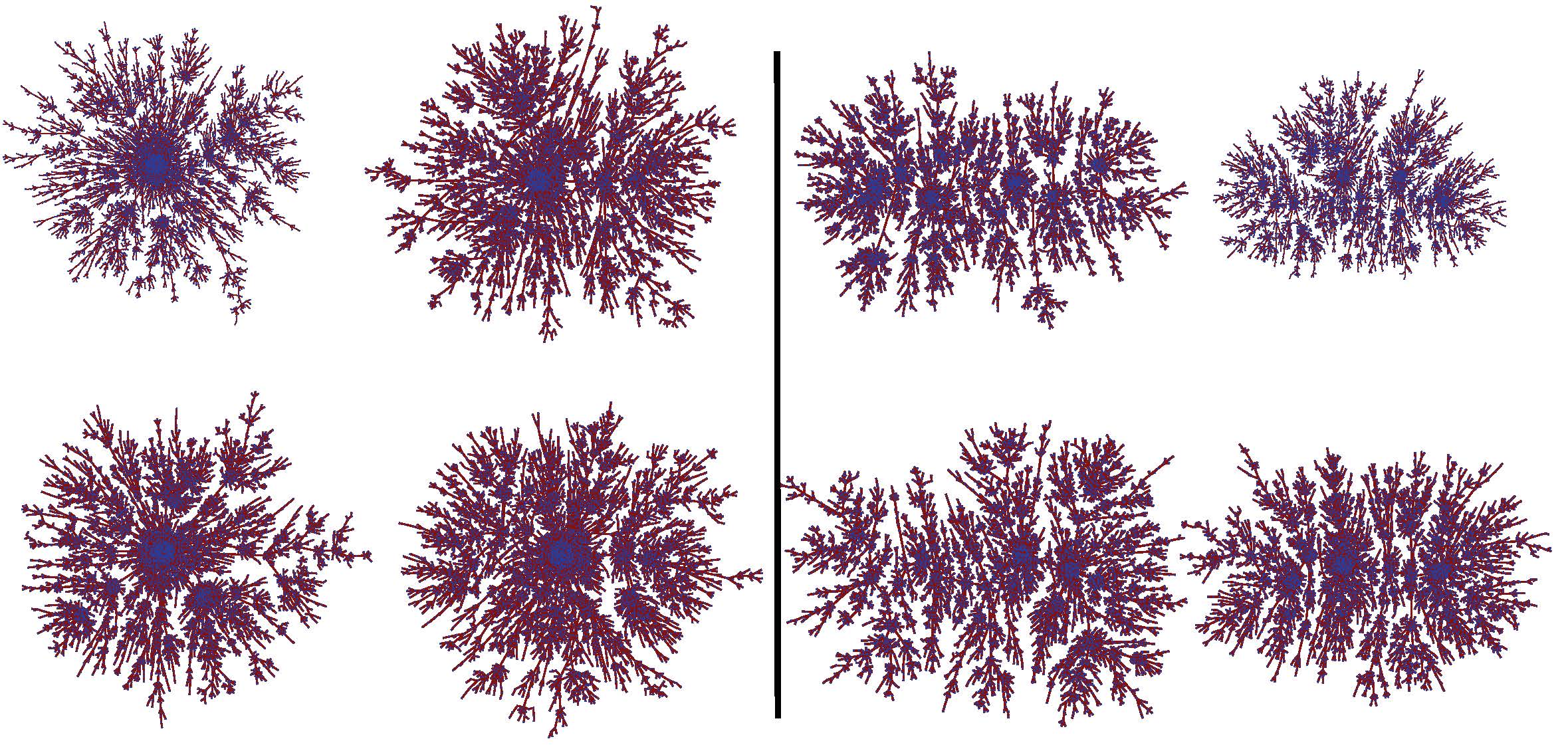
Bubeck, Mossel et Racz asked about how the seed has an influence on the asymptotic behavior of the process. For example, here are four realisations of trees with 5000 vertices, with a seed S_1 on the left and a seed S_2 on the right:
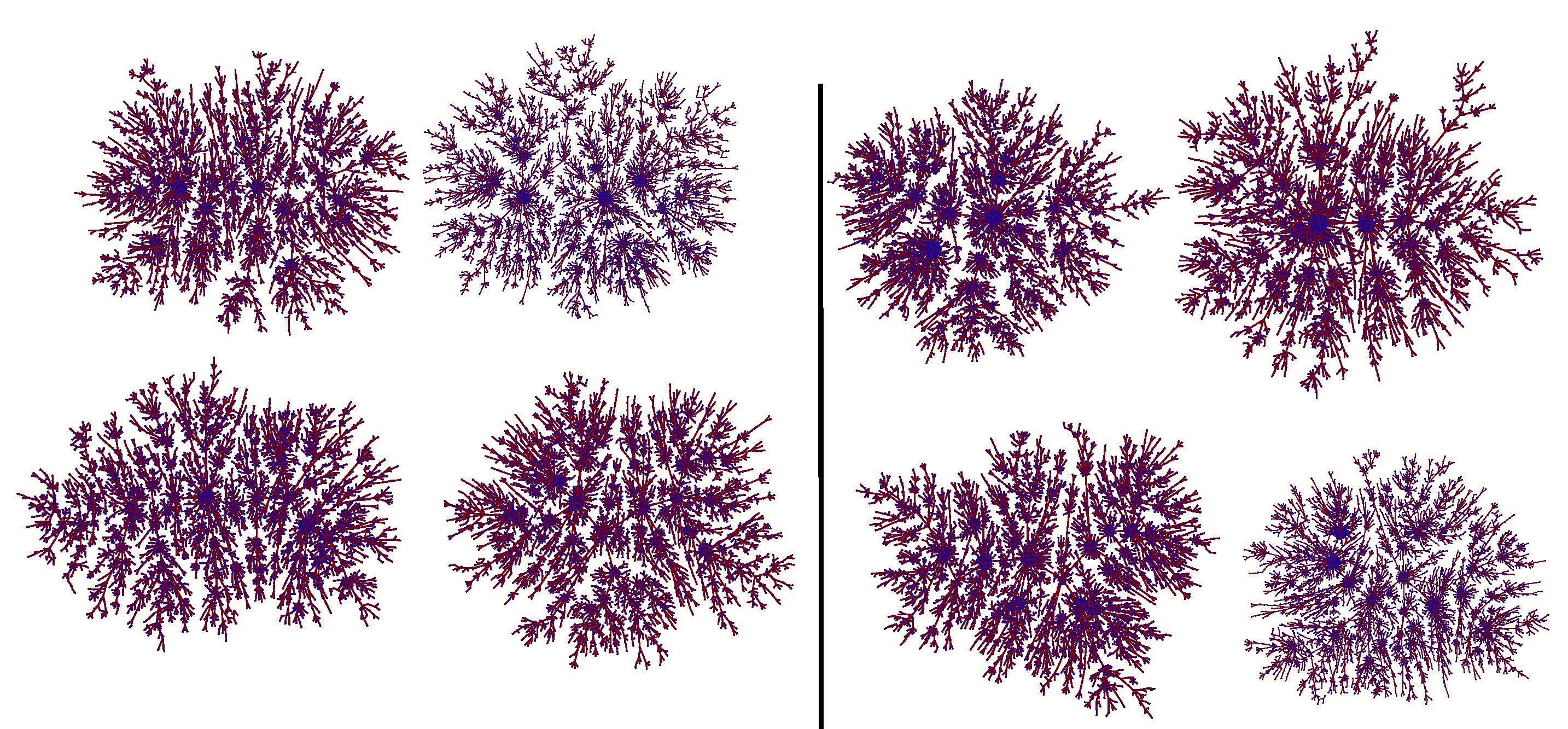
Do we have S_1=S_2 ? The answer is here. And now, here are four other realisations of trees with 5000 vertices, starting with a seed S'_1 on the left and a seed S'_2 on the right:
Do we have S'_1=S'_2 ? The answer is here.
In this article, we show that the seed has indeed an influence, and we show that the associated looptree converges, appropriately rescaled, to a limiting compact metric space, called the Brownian looptree, and which can be constructed as a quotient of the Brownian tree. Here is an embedding of a Brownian looptree, which looks a bit like Douady's rabbit:
Random maps
In this article, we show that the 1.5-stable looptree is the scaling limit of the boundary of large critical site-percolation clusters on random maps. From left to right and top to bottom: a large random triangulation, a finite neighborhood of Angel & Schramm's Uniform Infinite Planar Triangulation (UIPT), percolation interfaces of a site percolation on the UIPT, and percolation interfaces of a site percolation on a large random triangulation (last simulation by N. Curien) :
In a different direction, in this article, we study the lengths of the cycles obtained by cutting at fixed heights large Boltzmann triangulations with a boundary:
The case of Boltzmann triangulations is extended in this article to the dual maps of Boltzmann-type random maps with large faces, and the scaling limits are described by a one-parameter family of sequence-valued processes.3D Gallery
See here for some downloadable source files.
Artistic links
Here are some links to some other galleries: