Pulse shaping for atomic Bragg diffraction

Related publication: Leprince, C., Gondret, V., Lamirault, C., Dias, R., Marolleau, Q., Boiron, D., & Westbrook, C. I. Coherent coupling of momentum states: selectivity and phase control,Phys. Rev. A 111, 063304 (2025). PDF or HTML.

Bragg diffraction in atomic interferometry

In atomic interferometry, Bragg diffraction is used to coherently manipulate the paths of atoms or atomic clouds by applying a standing wave of light. This standing wave is created by the interference of two lasers that effectively acts as a diffraction grating for atomic waves.

Bragg diffraction can be understood as a two-photon transition coupling momenta separated by 2h/λ where λ is the period of the lattice created by the two lasers and h the Planck constant. The frequency detuning between the two lasers sets the momentum of the resonant class p which is coupled to p+2h/λ.

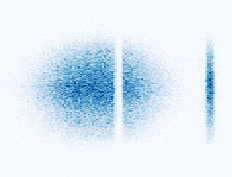
The laser power, which determines the Rabi frequency, defines the resonance width in momentum: the lower the power and the Rabi frequency, the narrower the width. For example, the image shown here represents the density of an atomic cloud. A Bragg pulse was used to deflect a narrow class of momenta. This image was taken 308 ms after the Bragg transition, so the atoms that were deflected have separated from the main cloud.

Mirror, mirror on the wall, who’s the fairest of them all?

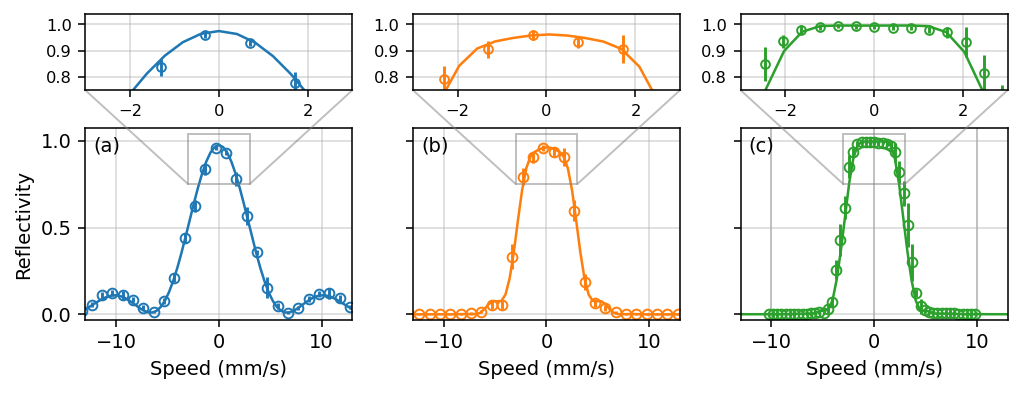
Depending on the duration of the light pulse, the atoms can be deflected with a 50% probability to perform a beam splitter or with a 100% probability to realize a mirror or deflector. A pulse whose temporal profile is square results in a momentum response containing side-lobes and which is not flat near the center of the efficiency curve. These drawbacks can be mitigated by choosing more complex pulse shapes. However, these more complex pulses require changing the sign of the two-photon Rabi frequency during the pulse, which is technically challenging.

In this project, we report the experimental realization of pulse-shaping techniques in the context of atomic Bragg diffraction. First, we implemented pulse-shaping methods originally developed in nuclear magnetic resonance spectroscopy to improve the reflectivity profile of the interferometer’s deflector. An example is shown in Figure 1: the simple constant pulse (a) is enhanced by modulating the laser pulses with a cardinal sine shape (b) and a ReBURP shape (c).

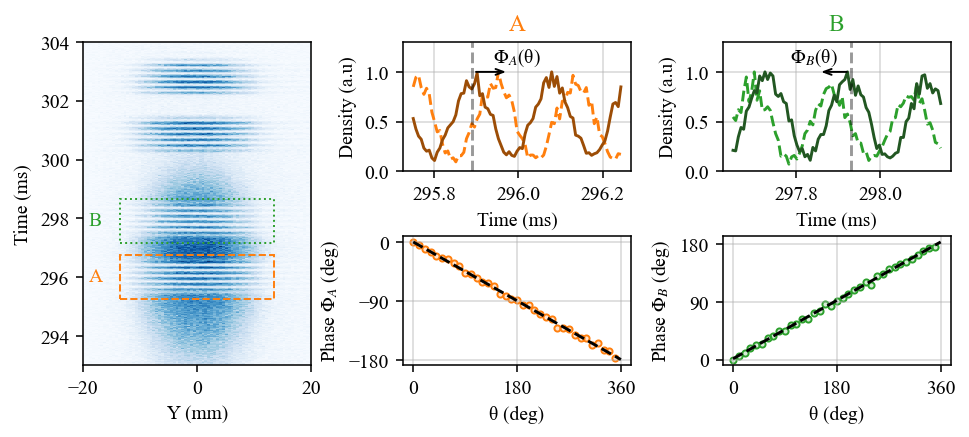
Figure 1: Reflectivity profile for three different pulse shapes: (a) has a square temporal profile, (b) a sinc shape, and (c) a Re-BURP shape. The square pulse results in a momentum response with side lobes and a non-flat region near the center of the efficiency curve. By Fourier analogy, a sinc temporal shape is expected to improve the reflectivity profile: we observe that the side lobes are suppressed, but the region at the center is not realy flat. A more advanced pulse shape, such as the Re-BURP pulse, achieves a much flatter reflectivity profile. Re-BURP stands for Refocusing Band-Selective Pulse with Uniform Response and Phase.

A robust interferometer to probe nonlocality

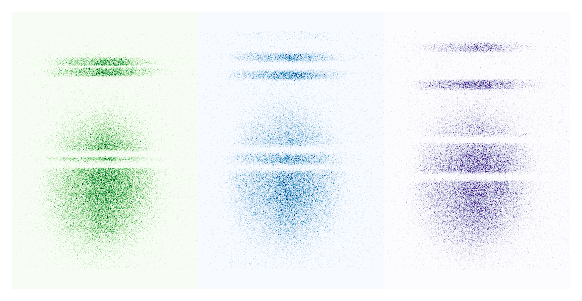
Second, we demonstrate that by modulating the Rabi frequency with a cosine function, we can address two distinct momentum classes whose separation in momentum is proportional to the modulation frequency. On this figure, we see that two distinct momentum classes can be deflected with this technique : the larger the frequency of the modulation, the larger the momentum difference between the two doublets. This enables the operation of two parallel interferometers, with each arm having a phase shift of plus or minus half the modulation phase. The main advantage of this technique is having a common rejection mode between the two interferometers, making them insensitive to phase fluctuations caused by the laser’s optical paths. This can be seen on the good visibility of the interference fringes in Fig. 2. We propose using such an interferometer with a momentum-entangled source of atoms to probe non-locality.

Figure 2: We demonstrate phase control of four-mode interferometer realizing a Ramsey interferometer. The phase imprinted on each interferometer, labeled A and B, depends on the phase of the modulation.