Growth dynamics of Faraday waves

Related publication: Gondret V, Dias R, Lamirault C, et al., Parametric pair production of collective excitations in a Bose-Einstein condensate, arXiv:2506.22024 (2025), PDF or HTML.

Pattern formation

It was first noted by M. Faraday in 1831 that when a fluid is vertically shaken, a pattern can appear at the fluid’s surface. The frequency of the excited modes is related to the spatial frequency of the resulting pattern via the fluid’s dispersion relation and appears at half the excitation frequency — a signature of parametric resonance. While Faraday’s original experiments were conducted with water, similar patterns can also be observed in Bose-Einstein condensates (BECs), which are quantum fluids.

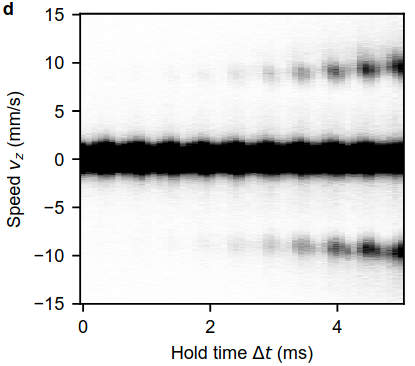
In our work, we induce transverse oscillations in the radial (transverse) confinement of an elongated BEC. These oscillations periodically modulate the longitudinal dispersion relation, resulting in the formation of a longitudinal density pattern — see the in situ density images shown above. As time progresses, the pattern becomes increasingly pronounced. However, we measure the quantum state in momentum space using a single-particle detector. When the gas is released, the collective excitation quanta are converted to witness atoms which carry the information of the state and escape from the BEC. This allows us to directly probe the Fourier transform of the spatial pattern. The time evolution of the 1D momentum density profile of the gas is shown in the figure. The pattern manifests as two sidebands at ±10 mm/s on either side of the central high-density peak at v=0 mm/s.

Growth of the pattern

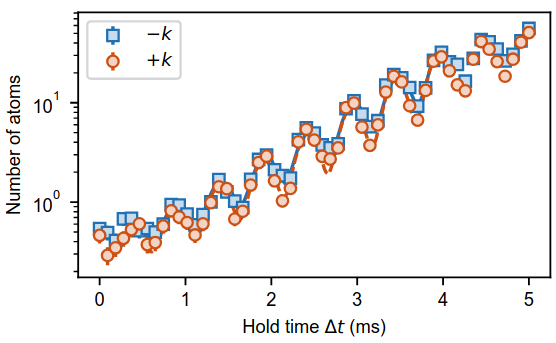
We have investigated in detail the growth dynamics of the two sidebands: the time evolution of the number of atoms which occupy them, shown in the figure, increases exponentially with a pronounced oscillation. The number of atoms in the two opposite sidebands are approximately the same, which witnesses that pairs are created in a correlated manner. In another study, we have shown that this correlation is so strong that it is non-classical: opposite momentum quasiparticles are entangled.

The exponential feature of the growth is characterized by a growth rate, that we can measure under different excitations procedures. We can compare the experimentally measured growth rate to the one which is predicted within Bogoliubov theory. In this description, the BEC acts as an infinite reservoir for quasiparticles which do not interact. However, in our system, quasiparticles do interact and this interaction reduces the effective growth rate of the pattern.

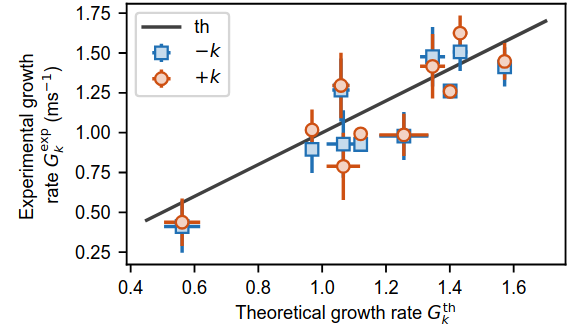
We have compared the noninteracting theoretical prediction (x axis) to the measured growth rates (y axis) and we found a very good agreement, see the Figure. This agreement confirms the smallness of the interaction between quasiparticles in such an elongated Bose gas. In the limit where the system is purely one dimensional, collective excitation cannot decay because the system is integrable. Still, in our condition, the reduction we observe are compatible with the recent prediction of Micheli & Robertson (2022). Future works will try to repeat the experiment to reduce the errorbars on the growth rate measurement to better quantify the reduction of the growth due to quasiparticle interactions.

The last part of the paper discusses the presence of the oscillation in the growth. We show that these oscillation stems from two ingredients: the fact that quasiparticles are created in a pairwise manner and the transfer of the collective excitation state to the atomic wavefunction, which is detected.