Source : Mardia, K.V., Kent, J.T., Bibby, J.M., Multivariate Analysis, Academic Press, London 1979.
Dans certaines situations, nous pouvons mesurer précisement la distance de deux objets quand ils sont proches, mais pas quand ils sont éloignés. Les distances modérées et les grandes distances apparaissent alors identiques. Ce mélange de toutes les grandes distances tend à placer les objets éloignés proches les uns des autres et a été appelé "effet fer à cheval" (horseshoe effect) par D.G. Kendall (1971).
L'exemple donné ici est dû à Kendall :
La matrice de similarités, de taille 51x51 est donnée par :
c(r,r) = 9
c(r,s) = 8 si 1 <= |r-s| <= 3
...
c(r,s) = 1 si 22 <= |r-s| <= 24
c(r,s) = 0 si |r-s| >= 25
Cette matrice est calculée dans le fichier horseshoe-effect.xls. On y trouve également une matrice de distances calculées à l'aide de la formule ;
d(r,s) = Racine[c(r,r) - 2 c(r, s) + c(s, s)]
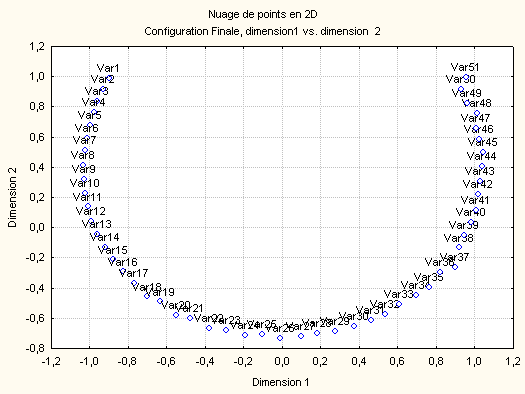
Le calcul du MDS est fait dans le classeur Statistica horseshoe-effect.stw. Il faut noter que le traitement fait par Statistica correspond au MDS non métrique. Il conduit à la représentation graphique suivante :
