On considère g populations différentes (facteur G à g niveaux), et g échantillons de sujets tirés au hasard dans ces populations. Le plan d'expérience correspondant est donc du type S<G>.
Sur chaque sujet, on observe p variables dépendantes X1, X2, ..., Xp.
On dispose des moyennes, variances et covariances des variables X1, X2, ..., Xp dans chacun des échantillons. On suppose par ailleurs que les hypothèses de normalité des variables dans chacune des populations, et d'égalité des variances et covariances observées dans les différentes populations peuvent être retenues. Ainsi, on peut supposer que les variables (X1, X2, ..., Xp) sont distribuées selon des lois multinormales de mêmes paramètres (hormis les moyennes) dans chacune des populations parentes.
Les estimations des variances et covariances (communes) sont obtenues comme moyennes pondérés de ces mêmes paramètres observés sur les échantillons (cf. exemple de calcul ci-dessous).
Exemple. Données "Iris" de Fisher.
On a noté, pour 150 iris, l'espèce (setosa, versicolor, virginica) et 4
variables numériques : la longueur et la largeur des sépales, la
longueur et la largeur des pétales. Pour chaque espèce, on dispose de
50 observations. Les 25 premières observations de chaque espèce vont
contituer l'ensemble d'apprentissage, tandis que les 25 observations
restantes seront classifiées à l'aide des résultats de l'analyse
discriminante. La classification ainsi obtenue pourra ainsi être
comparée aux données réelles.
| Sepal L | Sepal W | Petal L | Petal W |
Type Iris
|
Type Iris 2
|
|
| 1 | 5,1 | 3,5 | 1,4 | 0,2 |
setosa
|
setosa
|
| 2 | 4,9 | 3 | 1,4 | 0,2 |
setosa
|
setosa
|
| 3 | 4,7 | 3,2 | 1,3 | 0,2 |
setosa
|
setosa
|
| 4 | 4,6 | 3,1 | 1,5 | 0,2 |
setosa
|
setosa
|
| 5 | 5 | 3,6 | 1,4 | 0,2 |
setosa
|
setosa
|
| 6 | 5,4 | 3,9 | 1,7 | 0,4 |
setosa
|
setosa
|
| 7 | 4,6 | 3,4 | 1,4 | 0,3 |
setosa
|
setosa
|
| 8 | 5 | 3,4 | 1,5 | 0,2 |
setosa
|
setosa
|
| 9 | 4,4 | 2,9 | 1,4 | 0,2 |
setosa
|
setosa
|
| 10 | 4,9 | 3,1 | 1,5 | 0,1 |
setosa
|
setosa
|
| 11 | 5,4 | 3,7 | 1,5 | 0,2 |
setosa
|
setosa
|
| 12 | 4,8 | 3,4 | 1,6 | 0,2 |
setosa
|
setosa
|
| 13 | 4,8 | 3 | 1,4 | 0,1 |
setosa
|
setosa
|
| 14 | 4,3 | 3 | 1,1 | 0,1 |
setosa
|
setosa
|
| 15 | 5,8 | 4 | 1,2 | 0,2 |
setosa
|
setosa
|
| 16 | 5,7 | 4,4 | 1,5 | 0,4 |
setosa
|
setosa
|
| 17 | 5,4 | 3,9 | 1,3 | 0,4 |
setosa
|
setosa
|
| 18 | 5,1 | 3,5 | 1,4 | 0,3 |
setosa
|
setosa
|
| 19 | 5,7 | 3,8 | 1,7 | 0,3 |
setosa
|
setosa
|
| 20 | 5,1 | 3,8 | 1,5 | 0,3 |
setosa
|
setosa
|
| 21 | 5,4 | 3,4 | 1,7 | 0,2 |
setosa
|
setosa
|
| 22 | 5,1 | 3,7 | 1,5 | 0,4 |
setosa
|
setosa
|
| 23 | 4,6 | 3,6 | 1 | 0,2 |
setosa
|
setosa
|
| 24 | 5,1 | 3,3 | 1,7 | 0,5 |
setosa
|
setosa
|
| 25 | 4,8 | 3,4 | 1,9 | 0,2 |
setosa
|
setosa
|
| 26 | 5 | 3 | 1,6 | 0,2 |
setosa
|
|
| 27 | 5 | 3,4 | 1,6 | 0,4 |
setosa
|
|
| 28 | 5,2 | 3,5 | 1,5 | 0,2 |
setosa
|
|
| 29 | 5,2 | 3,4 | 1,4 | 0,2 |
setosa
|
|
| 30 | 4,7 | 3,2 | 1,6 | 0,2 |
setosa
|
|
| 31 | 4,8 | 3,1 | 1,6 | 0,2 |
setosa
|
|
| 32 | 5,4 | 3,4 | 1,5 | 0,4 |
setosa
|
|
| 33 | 5,2 | 4,1 | 1,5 | 0,1 |
setosa
|
|
| 34 | 5,5 | 4,2 | 1,4 | 0,2 |
setosa
|
|
| 35 | 4,9 | 3,1 | 1,5 | 0,2 |
setosa
|
|
| 36 | 5 | 3,2 | 1,2 | 0,2 |
setosa
|
|
| 37 | 5,5 | 3,5 | 1,3 | 0,2 |
setosa
|
|
| 38 | 4,9 | 3,6 | 1,4 | 0,1 |
setosa
|
|
| 39 | 4,4 | 3 | 1,3 | 0,2 |
setosa
|
|
| 40 | 5,1 | 3,4 | 1,5 | 0,2 |
setosa
|
|
| 41 | 5 | 3,5 | 1,3 | 0,3 |
setosa
|
|
| 42 | 4,5 | 2,3 | 1,3 | 0,3 |
setosa
|
|
| 43 | 4,4 | 3,2 | 1,3 | 0,2 |
setosa
|
|
| 44 | 5 | 3,5 | 1,6 | 0,6 |
setosa
|
|
| 45 | 5,1 | 3,8 | 1,9 | 0,4 |
setosa
|
|
| 46 | 4,8 | 3 | 1,4 | 0,3 |
setosa
|
|
| 47 | 5,1 | 3,8 | 1,6 | 0,2 |
setosa
|
|
| 48 | 4,6 | 3,2 | 1,4 | 0,2 |
setosa
|
|
| 49 | 5,3 | 3,7 | 1,5 | 0,2 |
setosa
|
|
| 50 | 5 | 3,3 | 1,4 | 0,2 |
setosa
|
|
| 51 | 7 | 3,2 | 4,7 | 1,4 |
versicolor
|
versicolor
|
| 52 | 6,4 | 3,2 | 4,5 | 1,5 |
versicolor
|
versicolor
|
| 53 | 6,9 | 3,1 | 4,9 | 1,5 |
versicolor
|
versicolor
|
| 54 | 5,5 | 2,3 | 4 | 1,3 |
versicolor
|
versicolor
|
| 55 | 6,5 | 2,8 | 4,6 | 1,5 |
versicolor
|
versicolor
|
| 56 | 5,7 | 2,8 | 4,5 | 1,3 |
versicolor
|
versicolor
|
| 57 | 6,3 | 3,3 | 4,7 | 1,6 |
versicolor
|
versicolor
|
| 58 | 4,9 | 2,4 | 3,3 | 1 |
versicolor
|
versicolor
|
| 59 | 6,6 | 2,9 | 4,6 | 1,3 |
versicolor
|
versicolor
|
| 60 | 5,2 | 2,7 | 3,9 | 1,4 |
versicolor
|
versicolor
|
| 61 | 5 | 2 | 3,5 | 1 |
versicolor
|
versicolor
|
| 62 | 5,9 | 3 | 4,2 | 1,5 |
versicolor
|
versicolor
|
| 63 | 6 | 2,2 | 4 | 1 |
versicolor
|
versicolor
|
| 64 | 6,1 | 2,9 | 4,7 | 1,4 |
versicolor
|
versicolor
|
| 65 | 5,6 | 2,9 | 3,6 | 1,3 |
versicolor
|
versicolor
|
| 66 | 6,7 | 3,1 | 4,4 | 1,4 |
versicolor
|
versicolor
|
| 67 | 5,6 | 3 | 4,5 | 1,5 |
versicolor
|
versicolor
|
| 68 | 5,8 | 2,7 | 4,1 | 1 |
versicolor
|
versicolor
|
| 69 | 6,2 | 2,2 | 4,5 | 1,5 |
versicolor
|
versicolor
|
| 70 | 5,6 | 2,5 | 3,9 | 1,1 |
versicolor
|
versicolor
|
| 71 | 5,9 | 3,2 | 4,8 | 1,8 |
versicolor
|
versicolor
|
| 72 | 6,1 | 2,8 | 4 | 1,3 |
versicolor
|
versicolor
|
| 73 | 6,3 | 2,5 | 4,9 | 1,5 |
versicolor
|
versicolor
|
| 74 | 6,1 | 2,8 | 4,7 | 1,2 |
versicolor
|
versicolor
|
| 75 | 6,4 | 2,9 | 4,3 | 1,3 |
versicolor
|
versicolor
|
| 76 | 6,6 | 3 | 4,4 | 1,4 |
versicolor
|
|
| 77 | 6,8 | 2,8 | 4,8 | 1,4 |
versicolor
|
|
| 78 | 6,7 | 3 | 5 | 1,7 |
versicolor
|
|
| 79 | 6 | 2,9 | 4,5 | 1,5 |
versicolor
|
|
| 80 | 5,7 | 2,6 | 3,5 | 1 |
versicolor
|
|
| 81 | 5,5 | 2,4 | 3,8 | 1,1 |
versicolor
|
|
| 82 | 5,5 | 2,4 | 3,7 | 1 |
versicolor
|
|
| 83 | 5,8 | 2,7 | 3,9 | 1,2 |
versicolor
|
|
| 84 | 6 | 2,7 | 5,1 | 1,6 |
versicolor
|
|
| 85 | 5,4 | 3 | 4,5 | 1,5 |
versicolor
|
|
| 86 | 6 | 3,4 | 4,5 | 1,6 |
versicolor
|
|
| 87 | 6,7 | 3,1 | 4,7 | 1,5 |
versicolor
|
|
| 88 | 6,3 | 2,3 | 4,4 | 1,3 |
versicolor
|
|
| 89 | 5,6 | 3 | 4,1 | 1,3 |
versicolor
|
|
| 90 | 5,5 | 2,5 | 4 | 1,3 |
versicolor
|
|
| 91 | 5,5 | 2,6 | 4,4 | 1,2 |
versicolor
|
|
| 92 | 6,1 | 3 | 4,6 | 1,4 |
versicolor
|
|
| 93 | 5,8 | 2,6 | 4 | 1,2 |
versicolor
|
|
| 94 | 5 | 2,3 | 3,3 | 1 |
versicolor
|
|
| 95 | 5,6 | 2,7 | 4,2 | 1,3 |
versicolor
|
|
| 96 | 5,7 | 3 | 4,2 | 1,2 |
versicolor
|
|
| 97 | 5,7 | 2,9 | 4,2 | 1,3 |
versicolor
|
|
| 98 | 6,2 | 2,9 | 4,3 | 1,3 |
versicolor
|
|
| 99 | 5,1 | 2,5 | 3 | 1,1 |
versicolor
|
|
| 100 | 5,7 | 2,8 | 4,1 | 1,3 |
versicolor
|
|
| 101 | 6,3 | 3,3 | 6 | 2,5 |
virginica
|
virginica
|
| 102 | 5,8 | 2,7 | 5,1 | 1,9 |
virginica
|
virginica
|
| 103 | 7,1 | 3 | 5,9 | 2,1 |
virginica
|
virginica
|
| 104 | 6,3 | 2,9 | 5,6 | 1,8 |
virginica
|
virginica
|
| 105 | 6,5 | 3 | 5,8 | 2,2 |
virginica
|
virginica
|
| 106 | 7,6 | 3 | 6,6 | 2,1 |
virginica
|
virginica
|
| 107 | 4,9 | 2,5 | 4,5 | 1,7 |
virginica
|
virginica
|
| 108 | 7,3 | 2,9 | 6,3 | 1,8 |
virginica
|
virginica
|
| 109 | 6,7 | 2,5 | 5,8 | 1,8 |
virginica
|
virginica
|
| 110 | 7,2 | 3,6 | 6,1 | 2,5 |
virginica
|
virginica
|
| 111 | 6,5 | 3,2 | 5,1 | 2 |
virginica
|
virginica
|
| 112 | 6,4 | 2,7 | 5,3 | 1,9 |
virginica
|
virginica
|
| 113 | 6,8 | 3 | 5,5 | 2,1 |
virginica
|
virginica
|
| 114 | 5,7 | 2,5 | 5 | 2 |
virginica
|
virginica
|
| 115 | 5,8 | 2,8 | 5,1 | 2,4 |
virginica
|
virginica
|
| 116 | 6,4 | 3,2 | 5,3 | 2,3 |
virginica
|
virginica
|
| 117 | 6,5 | 3 | 5,5 | 1,8 |
virginica
|
virginica
|
| 118 | 7,7 | 3,8 | 6,7 | 2,2 |
virginica
|
virginica
|
| 119 | 7,7 | 2,6 | 6,9 | 2,3 |
virginica
|
virginica
|
| 120 | 6 | 2,2 | 5 | 1,5 |
virginica
|
virginica
|
| 121 | 6,9 | 3,2 | 5,7 | 2,3 |
virginica
|
virginica
|
| 122 | 5,6 | 2,8 | 4,9 | 2 |
virginica
|
virginica
|
| 123 | 7,7 | 2,8 | 6,7 | 2 |
virginica
|
virginica
|
| 124 | 6,3 | 2,7 | 4,9 | 1,8 |
virginica
|
virginica
|
| 125 | 6,7 | 3,3 | 5,7 | 2,1 |
virginica
|
virginica
|
| 126 | 7,2 | 3,2 | 6 | 1,8 |
virginica
|
|
| 127 | 6,2 | 2,8 | 4,8 | 1,8 |
virginica
|
|
| 128 | 6,1 | 3 | 4,9 | 1,8 |
virginica
|
|
| 129 | 6,4 | 2,8 | 5,6 | 2,1 |
virginica
|
|
| 130 | 7,2 | 3 | 5,8 | 1,6 |
virginica
|
|
| 131 | 7,4 | 2,8 | 6,1 | 1,9 |
virginica
|
|
| 132 | 7,9 | 3,8 | 6,4 | 2 |
virginica
|
|
| 133 | 6,4 | 2,8 | 5,6 | 2,2 |
virginica
|
|
| 134 | 6,3 | 2,8 | 5,1 | 1,5 |
virginica
|
|
| 135 | 6,1 | 2,6 | 5,6 | 1,4 |
virginica
|
|
| 136 | 7,7 | 3 | 6,1 | 2,3 |
virginica
|
|
| 137 | 6,3 | 3,4 | 5,6 | 2,4 |
virginica
|
|
| 138 | 6,4 | 3,1 | 5,5 | 1,8 |
virginica
|
|
| 139 | 6 | 3 | 4,8 | 1,8 |
virginica
|
|
| 140 | 6,9 | 3,1 | 5,4 | 2,1 |
virginica
|
|
| 141 | 6,7 | 3,1 | 5,6 | 2,4 |
virginica
|
|
| 142 | 6,9 | 3,1 | 5,1 | 2,3 |
virginica
|
|
| 143 | 5,8 | 2,7 | 5,1 | 1,9 |
virginica
|
|
| 144 | 6,8 | 3,2 | 5,9 | 2,3 |
virginica
|
|
| 145 | 6,7 | 3,3 | 5,7 | 2,5 |
virginica
|
|
| 146 | 6,7 | 3 | 5,2 | 2,3 |
virginica
|
|
| 147 | 6,3 | 2,5 | 5 | 1,9 |
virginica
|
|
| 148 | 6,5 | 3 | 5,2 | 2 |
virginica
|
|
| 149 | 6,2 | 3,4 | 5,4 | 2,3 |
virginica
|
|
| 150 | 5,9 | 3 | 5,1 | 1,8 |
virginica
|
|
Les paramètres descriptifs des 75 individus de l'ensemble d'apprentissage sont alors donnés par :
Variable Groupé Moyennes du groupe
Moyenne setosa versicol virginic
Sepal L 5.8720 5.0280 6.0120 6.5760
Sepal W 3.0613 3.4800 2.7760 2.9280
Petal L 3.8040 1.4600 4.3120 5.6400
Petal W 1.2120 0.2480 1.3440 2.0440
Variable Groupé Ecart-type du groupe
EcarType setosa versicol virginic
Sepal L 0.5730 0.4005 0.5480 0.7242
Sepal W 0.3609 0.3686 0.3527 0.3612
Petal L 0.4668 0.1979 0.4438 0.6461
Petal W 0.1988 0.1046 0.2063 0.2551
On constate, par exemple que l'écart type "groupé" de la variable "Sepal L", ici notée X1 est donné par :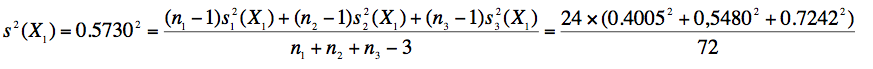
Matrice de covariance groupée
Sepal L Sepal W Petal L Petal W
Sepal L 0.32837
Sepal W 0.11636 0.13022
Petal L 0.21428 0.06457 0.21787
Petal W 0.04444 0.04305 0.04598 0.03952
Matrice de covariance du groupe setosa
Sepal L Sepal W Petal L Petal W
Sepal L 0.160433
Sepal W 0.118083 0.135833
Petal L 0.024083 0.006250 0.039167
Petal W 0.019433 0.022250 0.006583 0.010933
Matrice de covariance du groupe versicol
Sepal L Sepal W Petal L Petal W
Sepal L 0.300267
Sepal W 0.109467 0.124400
Petal L 0.186517 0.088633 0.196933
Petal W 0.051950 0.046517 0.064033 0.042567
Matrice de covariance du groupe virginic
Sepal L Sepal W Petal L Petal W
Sepal L 0.524400
Sepal W 0.121533 0.130433
Petal L 0.432250 0.098833 0.417500
Petal W 0.061933 0.060383 0.067333 0.065067
Soit ![]() la matrice gxg estimant les variances et covariances communes aux g populations. Soient m1, m2, ..., mg
les matrices px1 des moyennes des p variables dans les g populations.
L'écart quadratique entre les groupes i et j est donné par la formule :
la matrice gxg estimant les variances et covariances communes aux g populations. Soient m1, m2, ..., mg
les matrices px1 des moyennes des p variables dans les g populations.
L'écart quadratique entre les groupes i et j est donné par la formule :
![]()
Exemple de calcul
Sur l'exemple "Iris", les coefficients de la matrice des variances-covariances sont donnés par :
|
0,32837 |
0,11636 |
0,21428 |
0,04444 |
|
0,11636 |
0,13022 |
0,06457 |
0,04305 |
|
0,21428 |
0,06457 |
0,21787 |
0,04598 |
|
0,04444 |
0,04305 |
0,04598 |
0,03952 |
Les coefficients de son inverse sont :
|
12,1137 |
-7,9174 |
-11,2836 |
8,1308 |
|
-7,9174 |
17,3626 |
6,3010 |
-17,3413 |
|
-11,2836 |
6,3010 |
16,6887 |
-13,5920 |
|
8,1308 |
-17,3413 |
-13,5920 |
50,8647 |
La matrice des différences de moyennes entre les espèces setosa et versicolor est :
|
-0,984 |
|
0,704 |
|
-2,852 |
|
-1,096 |
Le calcul du produit de matrices ci-dessus conduit à un écart quadratique au carré de 98,84. Or, le tableau des écarts quadratiques donné par Minitab est :
Ecart quadratique entre les groupes
setosa versicol virginic
setosa 0.000 98.834 203.912
versicol 98.834 0.000 20.352
virginic 203.912 20.352 0.000
L'écart quadratique renseigne sur la séparation des populations par les variables considérées, et on peut démontrer que la probabilité de classement erroné est égal à l'expression :
![]()
dans laquelle ![]() désigne la fonction de répartition de la loi normale centrée réduite. Sur notre exemple :
désigne la fonction de répartition de la loi normale centrée réduite. Sur notre exemple :
![]()
Comme précédemment, soit ![]() la matrice gxg estimant les variances et covariances communes aux g populations. Soient m1, m2, ..., mg
les matrices px1 des moyennes des p variables dans les g populations et
soit x la matrice px1 des observations faites sur un individu à
classifier. La distance de Mahalanobis de cet individu au centre du
groupe j est donnée par :
la matrice gxg estimant les variances et covariances communes aux g populations. Soient m1, m2, ..., mg
les matrices px1 des moyennes des p variables dans les g populations et
soit x la matrice px1 des observations faites sur un individu à
classifier. La distance de Mahalanobis de cet individu au centre du
groupe j est donnée par :
![]()
L'individu est affecté au groupe correspondant à la distance la plus faible. On peut également calculer les probabilités d'appartenance a posteriori à l'aide des formules suivantes :
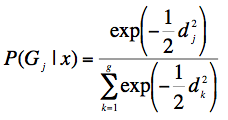
Exemple de calcul
Considérons l'individu No 78 du tableau "Iris". Il correspond aux valeurs suivantes des variables : (6.7, 3, 5, 1.7 ). Un calcul analogue à celui fait dans le paragraphe précédent conduit à :
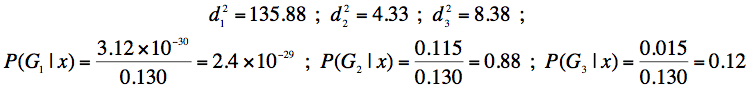
Cet individu est donc affecté au groupe 2, c'est-à-dire à l'espèce "versicolor".
Lorsque le nombre de variables est égal à 2, certains logiciels permettent de tracer des ellipses de concentration, qui sont les courbes de niveau de la distance d'un individu x quelconque au centre du groupe.
L'ensemble des points qui ont la même probabilité d'appartenance aux deux groupes d'indices j et k est l'hyperplan donné par l'équation :
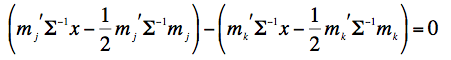
La fonction discriminante linéaire de la population j est définie par :
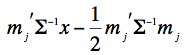
Les équations des hyperplans précédents sont obtenus en soustrayant deux à deux les fonctions discriminantes linéaires ainsi obtenues. On obtient ainsi g(g-1)/2 hyperplans correspondant aux classements possibles des g distances d'un individu aux centres des groupes.
On peut aussi remarquer que le classement d'un individu revient à l'affecter au groupe pour lequel la fonction discriminante linéaire est maximum.
Exemple. Dans le cas "Iris", les fonctions discriminantes linéaires produites par Minitab sont les suivantes :
Fonction discriminante linéaire jusqu'au groupe
setosa versicol virginic
Constante -78.505 -59.910 -89.958
Sepal L 18.901 13.123 9.459
Sepal W 25.508 4.461 -1.135
Petal L -13.816 3.347 10.589
Petal W -26.687 10.497 29.999
Lorsque le nombre de variables est réduit à 2, il est possible de représenter les équations précédentes par des droites d'un plan. En considérant les variables "Petal L" et "Petal W", on obtient un schéma du type suivant :
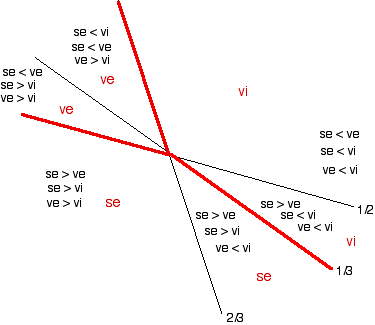
Comme pour la MANOVA, on introduit les matrices totale T, factorielle H et résiduelle E. Chacune de ces matrices est carrée d'ordre p, et symétrique. Pour chacune d'elles :
On recherche alors les valeurs propres et vecteurs propres de la matrice E-1H. On définit ainsi de nouvelles variables, combinaisons linéaires des variables observées, dites variables canoniques discriminantes. La première d'entre elles est telle que le rapport de la variance entre les groupes à la variance dans les groupes soit maximum. La seconde est indépendante de la première et vérifie la même propriété, une fois l'effet de la première pris en compte.
Statistica par exemple, donne l'expression des variables canoniques discriminantes en fonction des variables observées et en fonction des variables centrées réduites associées. Pour l'exemple "Iris", on obtient :
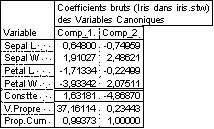
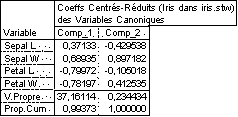
On peut alors calculer les valeurs des variables canoniques sur chacun des individus (scores canoniques des individus) et réaliser des graphiques tels que :
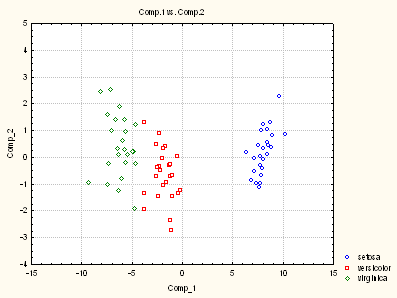
L'échantillon d'apprentissage des 75 iris est placé dans 5 colonnes d'une feuille de données. L'échantillon des individus à classer est placé dans des colonnes distinctes des précédentes. Avec un paramétrage convenable des dialogues, on obtient les résultats suivants :
Analyse discriminante
Méthode linéaire pour la réponse : Type Iri
Prédicteurs :Sepal L Sepal W Petal L Petal W
Groupe setosa versicol virginic
Dénombrement 25 25 25
Récapitulatif de classement
Placer dans ....Groupe vrai....
Groupe setosa versicol virginic
setosa 25 0 0
versicol 0 24 0
virginic 0 1 25
N Total 25 25 25
N Correct 25 24 25
Proportion 1.000 0.960 1.000
N = 75 N Correct = 74 Proportion correcte = 0.987
Ecart quadratique entre les groupes
setosa versicol virginic
setosa 0.000 98.834 203.912
versicol 98.834 0.000 20.352
virginic 203.912 20.352 0.000
Fonction discriminante linéaire jusqu'au groupe
setosa versicol virginic
Constante -78.505 -59.910 -89.958
Sepal L 18.901 13.123 9.459
Sepal W 25.508 4.461 -1.135
Petal L -13.816 3.347 10.589
Petal W -26.687 10.497 29.999
Variable Groupé Moyennes du groupe
Moyenne setosa versicol virginic
Sepal L 5.8720 5.0280 6.0120 6.5760
Sepal W 3.0613 3.4800 2.7760 2.9280
Petal L 3.8040 1.4600 4.3120 5.6400
Petal W 1.2120 0.2480 1.3440 2.0440
Variable Groupé Ecart-type du groupe
EcarType setosa versicol virginic
Sepal L 0.5730 0.4005 0.5480 0.7242
Sepal W 0.3609 0.3686 0.3527 0.3612
Petal L 0.4668 0.1979 0.4438 0.6461
Petal W 0.1988 0.1046 0.2063 0.2551
Matrice de covariance groupée
Sepal L Sepal W Petal L Petal W
Sepal L 0.32837
Sepal W 0.11636 0.13022
Petal L 0.21428 0.06457 0.21787
Petal W 0.04444 0.04305 0.04598 0.03952
Matrice de covariance du groupe setosa
Sepal L Sepal W Petal L Petal W
Sepal L 0.160433
Sepal W 0.118083 0.135833
Petal L 0.024083 0.006250 0.039167
Petal W 0.019433 0.022250 0.006583 0.010933
Matrice de covariance du groupe versicol
Sepal L Sepal W Petal L Petal W
Sepal L 0.300267
Sepal W 0.109467 0.124400
Petal L 0.186517 0.088633 0.196933
Petal W 0.051950 0.046517 0.064033 0.042567
Matrice de covariance du groupe virginic
Sepal L Sepal W Petal L Petal W
Sepal L 0.524400
Sepal W 0.121533 0.130433
Petal L 0.432250 0.098833 0.417500
Petal W 0.061933 0.060383 0.067333 0.065067
Récapitulatif des observations mal classées
Observation Vrai Prév Groupe Ecart Probabilité
Groupe Groupe quadratique
46 ** versicol virginic setosa 141.774 0.000
versicol 8.832 0.428
virginic 8.254 0.572
Prévision pour les observations de test
Groupe Depuis Ecart
Observation préd groupe quadratique Probabilité
1 setosa
setosa 2.888 1.000
versicol 79.958 0.000
virginic 179.303 0.000
2 setosa
setosa 1.309 1.000
versicol 80.342 0.000
virginic 176.363 0.000
...
28 versicol
setosa 135.876 0.000
versicol 4.330 0.883
virginic 8.380 0.117
...
75 virginic
setosa 164.094 0.000
versicol 12.435 0.027
virginic 5.273 0.973
On obtient ainsi les matrices de variances / covariances. En revanche, on n'obtient ni les fonctions linéaires discriminantes ni les variables canoniques.
Le classeur Statistica et les principaux résultats enregistrés au format .pdf se trouvent ci-dessous :
Résultats : partie 1, partie 2, partie 3.
Les résultats sont assez complets, mais il ne semble pas possible d'obtenir de manière simple la matrice des variances / covariances groupées.
Les procédures correspondantes se trouvent dans la library MASS
library(MASS)
data(iris3)
On définit l'ensemble d'apprentissage :
train <- rbind(iris3[1:25,,1], iris3[1:25,,2],iris3[1:25,,3] )
cl <- factor(c(rep("s",25), rep("c",25),rep("v",25)))
On exécute l'analyse proprement dite, dont les résultats sont stockés dans la variable z :
z <- lda(train, cl)
summary(z)
Length Class Mode
prior 3 -none- numeric
counts 3 -none- numeric
means 12 -none- numeric
scaling 8 -none- numeric
lev 3 -none- character
svd 2 -none- numeric
N 1 -none- numeric
call 3 -none- call
z$prior
c s v
0.3333333 0.3333333 0.3333333
z$counts
c s v
25 25 25
z$means
Sepal L. Sepal W. Petal L. Petal W.
c 6.012 2.776 4.312 1.344
s 5.028 3.480 1.460 0.248
v 6.576 2.928 5.640 2.044
z$scaling
LD1 LD2
Sepal L. -0.6480019 -0.7495864
Sepal W. -1.9102675 2.4862111
Petal L. 1.7133382 -0.2249931
Petal W. 3.9334180 2.0751059
z$lev
[1] "c" "s" "v"
z$svd
[1] 36.575964 2.905101
z$N
[1] 75
z$call
lda(x = train, grouping = cl)
On souhaite, par exemple, classer l'observation 26 :
aclasser <- iris3[26,,1]
aclasser
Sepal L. Sepal W. Petal L. Petal W.
5.0 3.0 1.6 0.2
res <- predict(z,aclasser)
summary(res)
Length Class Mode
class 1 factor numeric
posterior 3 -none- numeric
x 2 -none- numeric
L'observation est affectée au groupe "s" (setosa)
res$class
[1] s
Levels: c s v
On obtient ainsi les probabilités a posteriori :
res$posterior
c s v
[1,] 1.838998e-17 1 4.921413e-39
On peut aussi obtenir les scores de cette observation sur les variables canoniques discriminantes :
res$x
LD1 LD2
[1,] -7.074596 -1.102971
>
Référence bibliographique disponible sur Internet :
R. Palm, L'Analyse Discriminante Décisionnelle : principes et applications