On considère g populations différentes, et g échantillons de sujets tirés au hasard dans ces populations. Le plan d'expérience correspondant est donc du type S<G>.
Sur chaque sujet, on observe p variables dépendantes X1, X2, ..., Xp.
L'ANOVA à un facteur permet de tester l'égalité des moyennes dans les populations parentes, pour chaque variable dépendante prise isolément. La MANOVA, quant à elle, permet de tester l'égalité des vecteurs de moyennes dans les différentes populations parentes.
Autrement dit, notons ![]() la moyenne de la variable Xk dans le groupe j ; l'hypothèse nulle s'écrit alors :
la moyenne de la variable Xk dans le groupe j ; l'hypothèse nulle s'écrit alors :
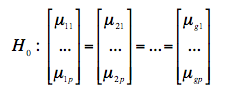
tandis que l'hypothèse alternative est la négation de H0 (test bilatéral).
La méthode de calcul de la statistique de test est analogue à celle de l'ANOVA, mais au lieu de considérer les sommes de carrés inter et sommes de carrés intra pour chaque variable, on introduit les matrices totale T, factorielle H et résiduelle E. Chacune de ces matrices est carrée d'ordre p, et symétrique. Pour chacune d'elles :
Mini-exemple. On a 2 groupes, 2 observations par groupe et 2 variables dépendantes, toutes deux de moyenne générale nulle. Les données sont les suivantes :
| VD1 | VD2 | |
| G1 |
-2
|
-3
|
| G1 |
0
|
1
|
| G2 |
-2
|
1
|
| G2 |
4
|
1
|
La matrice totale T (= E + H) est ici donnée par :
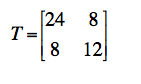
24 et 12 représentent 4 fois les variances de VD1 et VD2, tandis que 8 est égal à 4 fois la covariance de VD1 et VD2.
Les écarts inter-groupes et la matrice factorielle H sont donnés par :
|
|
VD1 | VD2 |
| G1 |
-1
|
-1
|
| G1 |
-1
|
-1
|
| G2 |
1
|
1
|
| G2 |
1
|
1
|
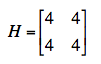
Les écarts intra-groupes (résidus) et la matrice résiduelle E sont ici :
| VD1 | VD2 | |
| G1 |
-1
|
-2
|
| G1 |
1
|
2
|
| G2 |
-3
|
0
|
| G2 |
3
|
0
|
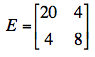
La statistique de test est le rapport lambda de Wilk défini par :
![]()
où la notation |M| désigne le déterminant de la matrice M.
Dans l'exemple étudié, on obtient :
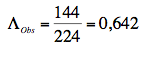
Cette valeur peut être transformée en un F de Fisher. Dans le cas étudié, on obtient F = 0,28. Les nombres de degrés de liberté à prendre en compte sont ddlA=2 et ddlB=1. La valeur trouvée n'est évidemment pas significative d'une différence entre les groupes.
On utilise la procédure Statistiques - ANOVA - ANOVA à un facteur. Il suffit d'indiquer plusieurs variables dépendantes dans la fenêtre de dialogue pour que le traitement effectué par Statistica soit une MANOVA. Considérons l'exemple (imaginaire) suivant :
| Groupe | VD1 | VD2 | |
| 1 | B | 3 | 2 |
| 2 | B | 4 | 6 |
| 3 | B | 5 | 12 |
| 4 | B | 6 | 9 |
| 5 | B | 7 | 6 |
| 6 | B | 7 | 11 |
| 7 | B | 10 | 4 |
| 8 | B | 12 | 10 |
| 9 | B | 14 | 6 |
| 10 | B | 16 | 6 |
| 11 | R | 4 | 13 |
| 12 | R | 6 | 14 |
| 13 | R | 7 | 11 |
| 14 | R | 12 | 12 |
| 15 | R | 13 | 13 |
| 16 | R | 15 | 10 |
| 17 | R | 16 | 9 |
| 18 | R | 17 | 3 |
| 19 | R | 18 | 5 |
| 20 | R | 19 | 4 |
On utilise le menu Statistiques - ANOVA - ANOVA à 1 facteur et on complète le dialogue comme suit :
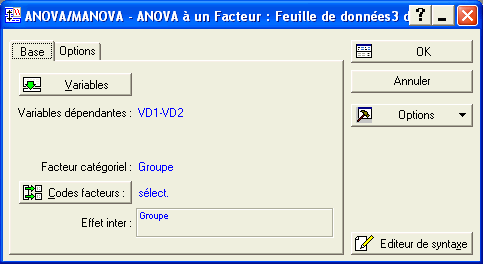
Le bouton "Tous les effets" permet d'obtenir le résultat suivant :
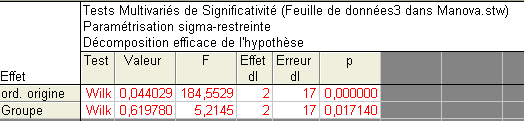
Le résultat du test montre une différence significative entre les deux groupes, pour l'ensemble des deux variables. On peut noter que l'ANOVA conduit à un résultat non significatif lorsqu'on considère chaque variable isolément. Mais les distributions des deux variables dans les deux groupes sont assez irrégulières, comme le montre le schéma ci-dessous, et il est vraisemblable que les données considérées contredisent les hypothèses de normalité des populations parentes, nécessaires pour justifier l'application de ces tests.
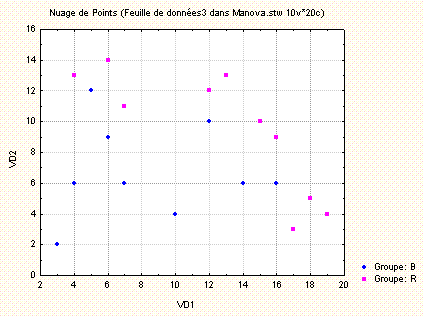
On considère l'exemple historique "Iris" de Fisher ou d'Anderson : on dispose d'échantillons de taille 50 de trois espèces d'iris. Les espèces d'iris sont : setosa, versicolor et virginica. Les variables dépendantes sont la longueur des sépales, la largeur des sépales, la longueur des pétales et la largeur des pétales.
data(iris)
iris
Sepal.Length Sepal.Width Petal.Length Petal.Width Species
1 5.1 3.5 1.4 0.2 setosa
2 4.9 3.0 1.4 0.2 setosa
...
150 5.9 3.0 5.1 1.8 virginica
On place les 4 VD dans un data.frame convenable :
Y <- cbind(iris$Sepal.Length,iris$Sepal.Width,iris$Petal.Length,iris$Petal.Width)
Le test de Wilk :
summary(manova(Y ~ Species, data=iris),test="Wilks")
Df Wilks approx F num Df den Df Pr(>F)
Species 2 0.023 199.145 8 288 < 2.2e-16 ***
Residuals 147
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
D'autres tests, également disponibles sous R :
summary(manova(Y ~ Species, data=iris),test="Hotelling-Lawley")
Df Hotelling-Lawley approx F num Df den Df Pr(>F)
Species 2 32.48 580.53 8 286 < 2.2e-16 ***
Residuals 147
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
summary(manova(Y ~ Species, data=iris),test="Roy")
Df Roy approx F num Df den Df Pr(>F)
Species 2 32.19 1166.96 4 145 < 2.2e-16 ***
Residuals 147
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
>
Référence bibliographique disponible sur Internet :