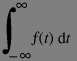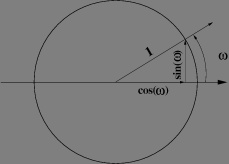
The cosinus function give the length of the edge of a right triangle of which the angle adjacent to the measured side is the argument and of which the longuest edge -the hypotenuse- is one.

May be you are used to express angles in degrees, scientists (as well as computers in fact) express angles in Radian (in short Rd: it is The Exception to the rule that units corresponding to a scientist name only take Capitals letters -such as Hz for Hertz, Pa for Pascal or Bq for Bequerel, but m for metter, s for second or g for gramme. There is no Dr Radian who worked on trigonometrics... perhaps that could worth be known for trivial pursuit, huh?) The angle is measured as the length along the circle of radius one from the horizontal to the triangle vertex. By definition of pi, one full turn correspond to 2pi hence 360° = 2pi Rd.
Here are some basic caracteristics on the periodicity and symetries of trigonometric functions:
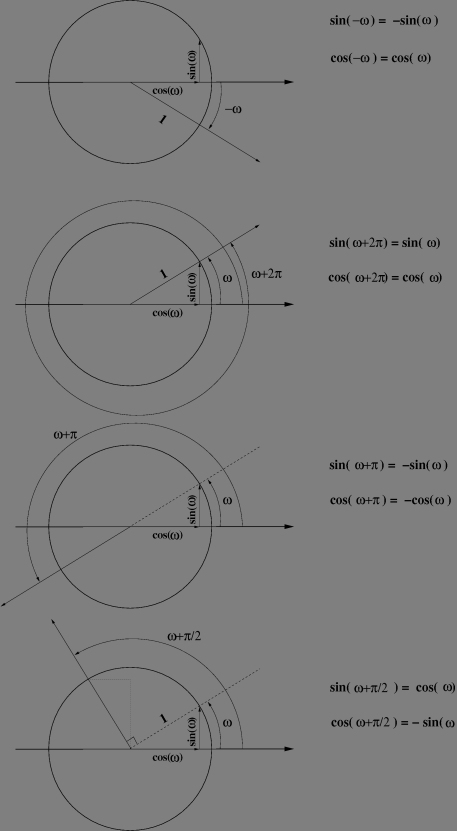
And here are some less basic properties you should know at least to pass you college exam:
You may play with ruler and compass to prove the above, but 2 by 2 matrix algebra or complex number are very efficient to derive these formulae rapidely.
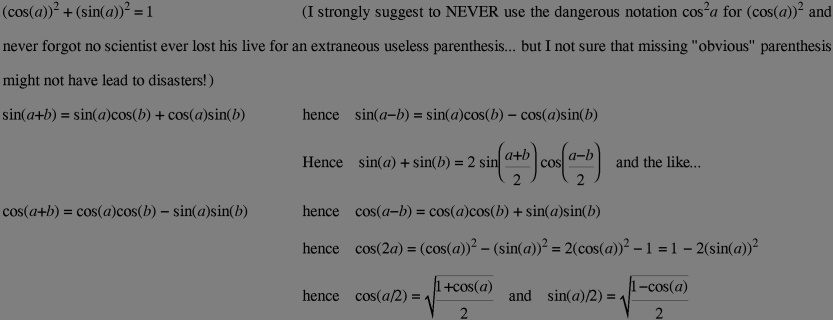
Eventually, some derivated trigonometric functions you may encounter in signal processing:
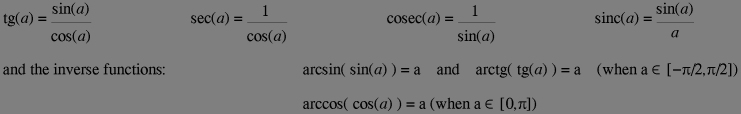
In order to simplify notations of repetitive operations, such as adding terms corresponding for successive values of a formula, the big sigma and big pi symbols have been introduced (sigma is the greek for s hence sum, pi is the greek for p hence product):
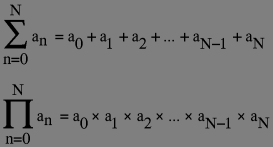
In case the result converges to a value as N grows, we may define the "infinite sum" which is obviously a concept (never ask a computer to effectively compute such a sum: none of us have the eternity available for whatever purpose indeed!) as the limit value. This is the occasion to introduce the limit operator:

In the Fourier transform definitions you will see the symbol of "continuous sum" namely "integration" (pronouced as "integral of...") it can be roughly defined as:
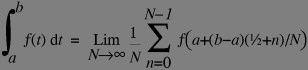
geometrically the integral is the area under the curve y=f(x) between the x axis and the bounds x=a and x=b. In fact integration is a science in its own, but this is the basic definition... Like the sigma and pi operators we can define the integration on an infinite interval (provided the value converges) such as: