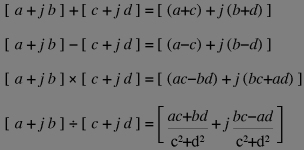
The idea of complex number is to give a field structure to the 2D plane in a similar -and compatible) manner than the field of real number can be assigned to a straight (1D) line. In a 1D space (line), addition is a translation and multiplication is a scaling with respect to the origin (zero) point of the line. In the 2D plane, addition is still a translation, multiplication by a real number (i.e. a complex number on the zero-one line) is still a scaling with respect to origin (zero) point. What to do with the multiplication with a number outside the real (zero-one) line ? Clearly multiplying a generic complex number z by 1 gives z itself, the natural idea is to say that: multiplying by a complex number is to scale and/or rotate with respect to the origin (zero) point in such a way that one is mapped to the given complex number. The complex number corresponding to a quarter of turn and no scaling plays an important role, comparable to that of 1, and therefore as its own symbol: j (sometimes, mathematicians -I was one in a previous life- use the letter i instead, but electronicians and physicists do not like because of possible mistake with intensity).
Note that twice a quarter is an half and turning the plane half a turn changes 1 into -1, hence j squared gives -1 (that is to say that j is the square root of -1 !). As any complex number can be written as a+bj with a and b real number, the basics four operations of complex algebra are:
This algebra have been invented for solving the third degree equation (remember the Cardan equations?). As a matter of fact the complex field proved to be much more complete than the real field, hence it is ubiquitous in mathematics and in physics and engineering as well.
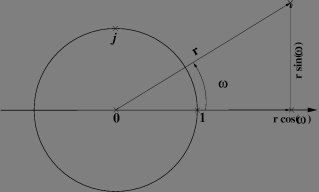
I am sure that the question you ask youself now is: And what about the square root? For that purpose, we shall link the complex number with the cosinus, sinus and exponential functions (it is worth it! Once you have understand this, deriving theses awfull trigonometric formulae becomes a child's game!). The idea is to use the distance r to zero and the angle theta to the zero-one line as coordinate for a complex number. The number can be written as:
Given this definition and this extra one 
. There is no magics behind, remember the series expansions of sin cos and exponential:
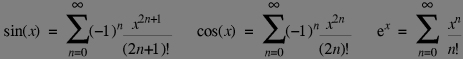
and apply the previous algebraic definitions. Now you now what means the formula 
that geeks wore on their white blouses at university!
About complex number, I shall add the definition of the conjugate of a complex number (there are several notations, over bar, star exponent or quote sign):
The main reason is to make distinction between positive and negative frequencies (as you remember, cos(kt) = cos(-kt) for all time, hence with real signals there is no difference between positive and negative frequencies). With complex numbers, we can define a signal with a pure frequency F as:
Where z0 is a nonzero complex number (giving the amplitude and phase at the origin of time t). With this definition, we can see the difference between two signals of opposite frequencies of which the real parts are identical:
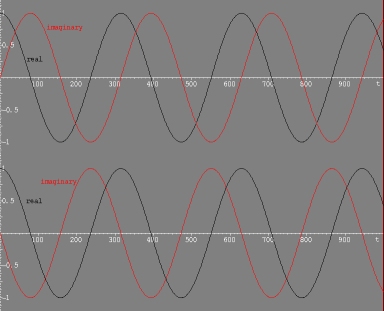
As you may know, light (as mentioned above radio wave are a form of light) is electromagnetic progressive wave. In its simplest form (technically that of a monochromatic linearly polarised light) the electrical field at a given point varies as a sinus function of time (and similarly the electrical field at a given time varies as a sinus function of the distance in the propagation direction. But even though the electrical field vanishes between the positive and negative alternances of the sinus function, the energy of the light does not vanish, indeed, there is a magnetic field that oscillate in a similar manner but has its peaks shifted by a quarter of period, hence its peaks corresponds to electrical field zeroes! What is the link with our complex pure frequencies? Simply that the two possible ways of shifting the magnetic field a quarter of wave with respect to the electric field correspond to propagation of the light energy in the two opposite directions!
Generally, the imaginary part of the signal is purely conceptual, but in some cases not at all: For example in the radar signal is digitized after I/Q demodulation -in that case radarists speak of "complex valued signal"-. Technically this means that the high frequency signal has been lowered to digitisable frequencies by multiplying it (on two different circuits) by the same reference frequency signals but shifted by a quarter of phase. With these two "real valued" signals we can determine if the high frequency signal was above or below the reference frequency (i.e. if the low frequency signal has a positive or negative frequency) by looking to the relative shift of the I channel and the Q channel. If they are as the black and red curves on the above plotings (top plot) the frequency is positive, in the other case (lower plot) the frequency is negative.