You will find here a short summary of some of my research projects. My main research activitiy focuses on water waves and interface dynamics both from experimental and theoretical perspective. When the opportunity arises I also enjoy to switch temporary to another topic! You can also check my publications for more details and the dissemination section for some videos of the experiments !

Current research projects

Interaction between deformable bodies and fluids

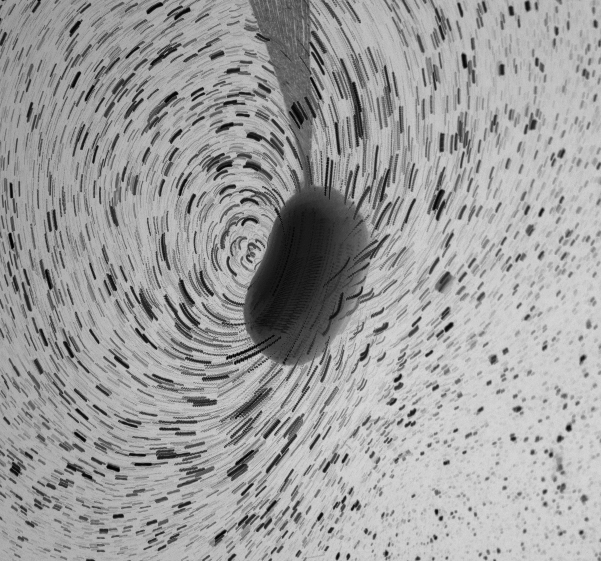
The trajectory of deformable object in a fluid is a fascinating question as it results in subtle interactions between the object's shape and the fluid's flow. I have recently developped an experiment in which a ball is straddled at the water surface through a deformable string. Although simple, this experimental setup reserves many surprises due to the interplay between the string's deformation and the generated flow. We uncovered in particular the existence of sel-trapped states in which the ball traps itself in the flow it generates !

The spinorial ball

Half-integer spin is generally introduced in quantum physics lectures as an object that does not come back to its original state after one full turn but that does after two. Due to this context, it is often thought and considered as a purely quantum behavior. However, half-integer spin is more than anything a geometrical feature of the rotation groups. Together with S. Bernardet and D. Dumas, we have developped the spinorial ball to provide a macroscopic visualization of those concepts. It consists in a ball made of LED panel that display the complex components of a spinor under the action of rotations.

Phase switch and topology in parametric oscillators

Parametric oscillators consists in large subharmonic resonance of a pendulum driven externally by an oscillating field. Due to subharmonic response, the phase of the pendulum's oscillation can take two specific values separated by half a period, and the choice of one or the other phase depends on initial conditions. In a recent work, we have explored how a to switch from one phase state to the other using an external perturbation. A general theoretical framework is developped both in the linear and non-linear case, and a topological interpretation of the transition is discussed. We also conduct experiments using Faraday instability at the water surface.

Previous research projects

Dynamical stabilization and vibro-equilibrium

Kapitza's pendulum experiment consists in stabilizing a pendulum in its upside down position using a fast oscillating external forcing. Interestingly, high vibrations can also be used to stabilize fluids in unexpected positions. For vertical shaking, we have shown that liquid layers could be stabilized above an air layer, and that it is possible to float under such levitating layer ! When the shaking is performed along an arbitrary direction, new equilibrium positions can appear leading to stabilized liquid walls on which it is possible to surf !

Time-varying media for water waves

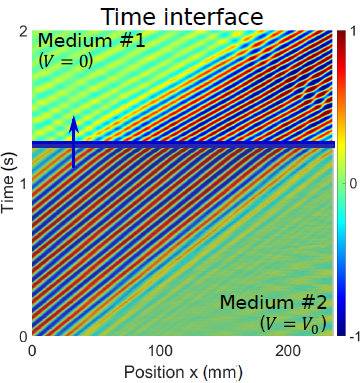
Time-varying media have recently emerged as a new method of control of waves by leveraging the temporal degrees of freedom. Nevertheless, experimental realizations remain challenging. We have shown that water waves could be controlled using high electric fields, and that the variation of the electric field along time results in an effective implementation of time-varying media with excellent control. This allowed us to perform large frequency conversion through linear process, and to study wave propagation in disordered time-vayring media.

Electrical control of water waves

Spatial control of water waves is commonly performed by placing solid inclusions in the fluid, which is heavily invasive and generally increases dissipation. To overcome those limitations, we explored a new way to control water waves using high elecric fields. The latter allow precise, non-invasive and reconfigurable refractive control that we used to focus, reflect or guide water waves ! water waves using