Tests abordés dans cette page : Kolmogorov-Smirnov, Lilliefors, Shapiro-Wilk, Anderson-Darling
Un test a été étalonné sur une population A de manière que sa distribution suive une loi normale de moyenne 13 et d'écart type 3. sur un échantillon de taille 10 issu d'une population B, on a observé les valeurs suivantes :
8.43 8.70 11.27 12.92 13.05 13.05 13.17 13.44 13.89 18.90
Ces valeurs sont-elles compatibles avec l'hypothèse selon laquelle la variable sous-jacente est distribuée selon une loi normale de moyenne 13 et d'écart type 3 ?
On peut utiliser la commande ks.test du package "stats" :
> X1 <- c(8.43, 8.70, 11.27, 12.92, 13.05, 13.05, 13.17, 13.44, 13.89, 18.90)
> ks.test(X1,"pnorm",mean=13, sd=3)
One-sample Kolmogorov-Smirnov testdata: X1
D = 0.2834, p-value = 0.3982
alternative hypothesis: two-sided
Warning message:
cannot compute correct p-values with ties in: ks.test(X1, "pnorm", mean = 13, sd = 3)
On peut éviter le message d'avertissement concernant les ex aequo en modifiant légèrement l'une des valeurs 13.05 :
> X1 <- c(8.43, 8.70, 11.27, 12.92, 13.05, 13.050001, 13.17, 13.44, 13.89, 18.90)
> ks.test(X1,"pnorm",mean=13, sd=3)
One-sample Kolmogorov-Smirnov test
data: X1
D = 0.2834, p-value = 0.3326
alternative hypothesis: two-sided
On observe effectivement une valeur du niveau de significativité assez différente de la précédente.
Calcul à la main : On calcule, pour chaque valeur observée Xi, les fréquences cumulées F(X < Xi) et F(X <= Xi).
On calcule également les fréquences cumulées théoriques aux points Xi pour la loi normale de paramètres m=13 et s=3. On calcule enfin les écarts entre les fréquences cumulées expérimentales et les fréquences cumulées théoriques. La valeur de D est le maximum de ces écarts :
|
X
|
F(X < Xi)
|
F(X <= Xi)
|
Theo
|
Ecart -
|
Ecart +
|
|
8,43
|
0
|
0,1
|
0,0638
|
0,0638
|
0,0362
|
|
8,7
|
0,1
|
0,2
|
0,0759
|
0,0241
|
0,1241
|
|
11,27
|
0,2
|
0,3
|
0,2821
|
0,0821
|
0,0179
|
|
12,92
|
0,3
|
0,4
|
0,4894
|
0,1894
|
0,0894
|
|
13,05
|
0,4
|
0,6
|
0,5066
|
0,1066
|
0,0934
|
|
13,17
|
0,6
|
0,7
|
0,5226
|
0,0774
|
0,1774
|
|
13,44
|
0,7
|
0,8
|
0,5583
|
0,1417
|
0,2417
|
|
13,89
|
0,8
|
0,9
|
0,6166
|
0,1834
|
0,2834
|
|
18,9
|
0,9
|
1
|
0,9754
|
0,0754
|
0,0246
|
On retrouve ainsi D = 0.2834
Sur un échantillon de taille 10, on a observé les valeurs suivantes d'une VD numérique :
8, 9, 9, 10, 10, 10, 11, 13, 14, 14.
Est-il légitime de supposer que la distribution de la VD dans la population parente suit une loi normale ?
Ici, la moyenne et l'écart type de la distribution théorique sont estimés à partir des 10 observations. Le test de Lilliefors est donc préférable au test de Kolmogorov-Smirnov.
Ce test n'est pas disponible "en standard" avec R, mais il se trouve dans le package "nortest" :
> library(nortest)
> X2 <- c(8, 9, 9, 10, 10, 10, 11, 13, 14, 14)
> lillie.test(X2)
Lilliefors (Kolmogorov-Smirnov) normality test
data: X2
D = 0.2451, p-value = 0.0903
Calcul à la main : la statistique de test se calcule de la même façon que celle du test de Kolmogorov-Smirnov.
> X3 <- c(5,5.5,5.5,6,14,16,16,17)
> ks.test(X3,"pnorm",mean=mean(X3),sd=sd(X3))
One-sample Kolmogorov-Smirnov test
data: X3
D = 0.2978, p-value = 0.4771
alternative hypothesis: two-sided
Warning message:
cannot compute correct p-values with ties in: ks.test(X3, "pnorm", mean = mean(X3), sd = sd(X3))
> lillie.test(X3)
Lilliefors (Kolmogorov-Smirnov) normality test
data: X3
D = 0.2978, p-value = 0.03534
> X3 <- c(5,5.5001,5.5002,6,14,16,16.0001,17)
> ks.test(X3,"pnorm",mean=mean(X3),sd=sd(X3))
One-sample Kolmogorov-Smirnov test
data: X3
D = 0.2978, p-value = 0.399
alternative hypothesis: two-sided
On constate, comme précédemment, que le niveau de significativité indiqué pour le test de Kolmogorov-Smirnov est très sensible à la présence d'ex aequo.
On reprend l'exemple illustrant le test de Lilliefors.
Sur un échantillon de taille 10, on a observé les valeurs suivantes d'une VD numérique :
8, 9, 9, 10, 10, 10, 11, 13, 14, 14.
Est-il légitime de supposer que la distribution de la VD dans la population parente suit une loi normale ?
Le test de Shapiro-Wilk est disponible dans le package "stats". La fonction correspondante est shapiro.test.
> X2 <- c(8, 9, 9, 10, 10, 10, 11, 13, 14, 14)
> shapiro.test(X2)
Shapiro-Wilk normality test
data: X2
W = 0.8849, p-value = 0.1485
On reprend l'exemple illustrant le test de Lilliefors.
Sur un échantillon de taille 10, on a observé les valeurs suivantes d'une VD numérique :
8, 9, 9, 10, 10, 10, 11, 13, 14, 14.
Est-il légitime de supposer que la distribution de la VD dans la population parente suit une loi normale ?
Le test d'Anderson-Darling est disponible dans le package "nortest". La fonction correspondante est ad.test.
> library(nortest)
> X2 <- c(8, 9, 9, 10, 10, 10, 11, 13, 14, 14)
> ad.test(X2)
Anderson-Darling normality test
data: X2
A = 0.5347, p-value = 0.1264
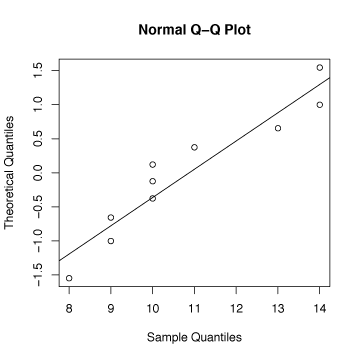
L'écart à la normalité peut être représenté par le graphique suivant :
> qqnorm(X2,datax=TRUE)
> qqline(X2,datax=TRUE)
