2.1 Estimation d'une moyenne par bootstrap

C'est le cas le plus simple et il est, en grande partie, sans intérêt, puisque l'on sait que la moyenne d'échantillon est un estimateur sans biais de la "vraie" moyenne. Nous allons le traiter sur l'exemple suivant :

On a observé la longueur (en dixièmes de millimètres) de la 3è rémige sur un échantillon de 40 pinsons des arbres.

x = (720, 680, 705, 600, 625, 680, 630, 650, 635, 640, 675, 620, 625, 700, 620, 600, 690, 615, 720, 655, 620, 640, 675, 665, 620, 630, 680, 660, 690, 720, 650, 680, 700, 685, 625, 690, 650, 645, 690, 670)

ou encore, en utilisant R :

rem <- c(720, 680, 705, 600, 625, 680, 630, 650, 635, 640, 675, 620, 625, 700, 620, 600, 690, 615, 720, 655, 620, 640, 675, 665, 620, 630, 680, 660, 690, 720, 650, 680, 700, 685, 625, 690, 650, 645, 690, 670)

La moyenne et l'erreur type estimés à partir de l'échantillon sont donnés par :

mean(rem) = 659.25 sd(rem)/sqrt(length(rem)) = 5.399282

On procède au ré-échantillonnage et on évalue la moyenne sur chaque échantillon tiré. Cette procédure est menée sous R.

2.2 Le bootstrap avec R

Dans la library "boot", on trouve une fonction boot() qui procède au tirage au sort (avec remise) des n indices retenus pour former l'échantillon bootstrap x_b* et qui calcule les B valeurs s(x_b*) avec b = 1, 2, ..., B. Ce dernier calcul est fait à partir d'une fonction définie par l'utilisateur et prenant deux paramètres. Dans l'utilisation élémentaire de cette fonction, ces paramètres sont d'une part le vecteur représentant l'échantillon de départ, d'autre part le vecteur de longueur n des indices retenus pour former l'échantillon bootstrap courant. Ainsi, pour estimer une moyenne par bootstrap, on pourra utiliser la fonction suivante :

moyenne <- function(d,w) {
n <- length(d)
return(sum(d[w[1:n]])/n)}

La fonction boot() produit un objet de classe "boot" (calculé ici avec B=500) :

library(boot)
rem.boot <- boot(rem,moyenne, R=500)

rem.boot$t0 donne la valeur du paramètre (ici la moyenne) sur l'échantillon de départ, rem.boot$t est le vecteur des R réplicats du paramètre obtenus par bootstrap. L'estimation bootstrap de la moyenne et l'erreur type correspondante peuvent être obtenues par :

print(mean(rem.boot$t))
[1] 659.0232
print(sd(rem.boot$t))
[1] 5.53912

Appliquée à un objet de la classe boot, la méthode print donne la valeur du paramètre sur l'échantillon de départ, le biais estimé de cette estimation et l'erreur standard calculée à partir des valeurs obtenues par bootstrap :

print(rem.boot)
ORDINARY NONPARAMETRIC BOOTSTRAP
Call:
boot(data = rem, statistic = moyenne, R = 500)
Bootstrap Statistics :
original bias std. error
t1* 659.25 -0.22675 5.53912

On peut aussi accéder au tableau des indices retenus pour chaque échantillon bootstrap :

> print(boot.array(rem.boot))
[,1] [,2] [,3] [,4] [,5] [,6] [,7] [,8] [,9] [,10] [,11] [,12] [,13] [,14] [,15] [,16] [,17] [,18]
[1,] 1 0 1 1 3 4 1 0 0 0 0 1 0 1 2 1 2 0
[2,] 0 1 2 1 1 0 1 0 0 1 1 3 2 0 0 0 3 2
[3,] 0 0 0 0 1 1 0 1 1 2 1 1 2 1 0 3 2 0

3.1 Présentation

Pour estimer un paramètre T de la variable X sur la population P, on dispose d'un estimateur biaisé t. Le biais de l'estimateur est défini par :

biais(t) = T - t c'est-à-dire : T = t + biais(t)

On calcule t sur l'échantillon de départ. Notons-le t(x). Puis, par bootstrap, on calcule t(x_b*) pour b = 1, 2, ... B, sur B échantillons bootstrap, et leur moyenne t*. Le biais de l'estimateur t est alors estimé par :

biais(t) = t - t*.

On en déduit une nouvelle estimation, non biaisée, du paramètre T sur la population :

T = t + biais(t) = 2 t - t*.

3.2 Exemple 1

Soit une variable X définie sur une population P, et pour laquelle on sait que la loi de distribution est une loi uniforme sur l'intervalle [0, A], avec A inconnu. On dispose d'un échantillon de taille n : x = (x₁, x₂, ..., x_n). L'estimateur du maximum de vraisemblance de A est : t = max(x₁, x₂, ..., x_n). Par bootstrap, on obtient t*, d'où la nouvelle estimation de A : A = 2 t - t*.

Sous R, on obtient par exemple :

# Charger la library boot
library(boot)

# 20 valeurs issues d'une loi uniforme sur [0,10]

x <- runif(20,min=0,max=10)

xmax <- max(x)

Maximum sur l'echantillon

print(xmax)
[1] 9.325259

valmax <- function(d,w) {
n <- length(d)
return(max(d[w[1:n]]))}

x.boot <- boot(x,valmax, R=500)

Le sommaire du bootstrap

print(x.boot)

ORDINARY NONPARAMETRIC BOOTSTRAP
Call:
boot(data = x, statistic = valmax, R = 500)
Bootstrap Statistics :
original bias std. error
t1* 9.325259 -0.3874595 0.5968421

Moyenne observee sur le bootstrap

print(mean(x.boot$t))
[1] 8.9378

Ecart type observe sur le bootstrap

print(sd(x.boot$t))
[1] 0.5968421

Correction du biais de l'estimateur par bootstrap

theta <- 2* xmax - mean(x.boot$t)
print(theta)
[1] 9.712718

3.3 Exemple 2

On sait que la vairance (non corrigée) d'un échantillon est un estimateur biaisé de la variance d'une variable sur une population. On reprend ici l'exemple des rémiges des pinsons (cf. paragraphe 2).

# Variance sur une population, ou variance non corrigée

L'estimateur non biaisé de la variance :

print(var(rem))
[1] 1166.090

La fonction "variance non corrigée" :

varp <- function(d){
n <- length(d)
res <- sum((d-mean(d))^2)/n
return(res)}

Variance non corrigée de l'échantillon :

print(varp(rem))
[1] 1136.938

Le bootstrap

varp.boot <- function(d,w) {
n <- length(d)
m <- sum(d[w[1:n]])/n
return(sum((d[w[1:n]]-m)^2)/n)}

rem.boot <- boot(rem,varp.boot, R=5000)

Moyenne des variances obtenues par bootstrap

print(mean(rem.boot$t))
[1] 1106.757

Correction du biais de l'estimateur par bootstrap

theta <- 2* varp(rem) - mean(rem.boot$t)
print(theta)
[1] 1167.118

On veut déterminer un intervalle de confiance pour un paramètre. Diverses méthodes ont été proposées pour déterminer un intervalle de confiance à partir des B valeurs obtenues par bootstrap et estimant ce paramètre. Par exemple (en notant a la valeur valeur alpha/2) :

- Méthode de l'erreur standard (standard bootstrap confidence interval) : on utilise la moyenne t* et l'erreur type s* du paramètre obtenues par bootstrap, et la loi normale (ou la loi de Student) pour construire l'intervalle : [t* + s* z_a, t* + s* z_1-a].

- Méthode des pourcentiles simples (simple percentile confidence interval) : on construit la fonction de répartition des valeurs (t*) obtenues par bootstrap et on prend comme bornes de l'intervalle le a-ième et le (1-a)-ième percentile.

La fonction boot.ci() de R permet d'obtenir 4 ou 5 intervalles de confiance calculés selon diverses méthodes. Sur l'exemple des rémiges de pinsons (cf. paragraphe 2), on obtient :

print(boot.ci(rem.boot))

BOOTSTRAP CONFIDENCE INTERVAL CALCULATIONS
Based on 500 bootstrap replicates
CALL :
boot.ci(boot.out = rem.boot)
Intervals :
Level Normal Basic
95% (649.1, 669.6 ) (649.4, 670.4 )
Level Percentile BCa
95% (648.1, 669.1 ) (648.3, 669.2 )
Calculations and Intervals on Original Scale
Warning message:
bootstrap variances needed for studentized intervals in: boot.ci(rem.boot)

Les méthodes utilisées semblent varier d'un auteur à l'autre et toutes ne sont sans doute pas correctes au niveau théorique. Ce paragraphe n'est donc qu'une version provisoire, destinée à évoluer.

5.1 Comparer une moyenne à une norme

Comme pour le test paramétrique habituel, on utilise la statistique : S = (moyenne estimée sur l'échantillon - moyenne de référence)/(erreur type empirique sur la moyenne estimée).

- On calcule la valeur s de la statistique S sur l'échantillon observé.

- On tire B échantillons par bootstrap, et pour chacun d'entre eux, on calcule la valeur s_b* statistique S, en évaluant la moyenne estimée et l'erreur type empirique à partir de l'échantillon bootstrap.

- On calcule la p-value bootstrap par :

p* = 1/B (Nombre de s_b* > s)

et on rejette H0 si p* < a/2 ou p* > 1 - a/2.

Exemple traité avec R :

Selon le département américain des statistiques sur l'emploi, en novembre 1998, la durée moyenne nationale d'inactivité était de 14.6 semaines. A la même date, le maire de Philadelphie a demandé une étude sur la situation, en termes de chômage, de Philadelphie et de sa périphérie. Sur un échantillon de 15 habitants sans emploi, le nombre de semaines d'inactivité était le suivant :

22, 19, 7, 37, 18, 11, 6, 22, 5, 20, 12, 1, 33, 26, 13

1) Calculer la moyenne et l'écart type de la variable "durée d'inactivité" sur l'échantillon étudié.

2) Effectuer un test d'hypothèses pour déterminer si la durée moyenne d'inactivité à Philadelphie est différente de la durée moyenne nationale, égale à 14.6 semaines. On utilisera un test bilatéral, avec un seuil de 5%.

# Moyenne de reference
m0 <- 14.6

Echantillon observe :
phiphi <- c(22, 19, 7, 37, 18, 11, 6, 22, 5, 20, 12, 1, 33, 26, 13)

mean(phiphi)
# [1] 16.8
sd(phiphi)
# [1] 10.34546
s <- (mean(phiphi)-m0)/(sd(phiphi)/sqrt(length(phiphi)))
s
# [1] 0.823604

# Fonction pour le bootstrap
stat_de_test <- function(d,w) {
n <- length(d)
ech <- c(d[w[1:n]])
return((mean(ech)-m0)/(sd(ech)/sqrt(length(ech))))
}

# Nombre de bootstrap

B <- 1000

# Execution du bootstrap
phiphi.boot <- boot(phiphi, statistic=stat_de_test, R=B)
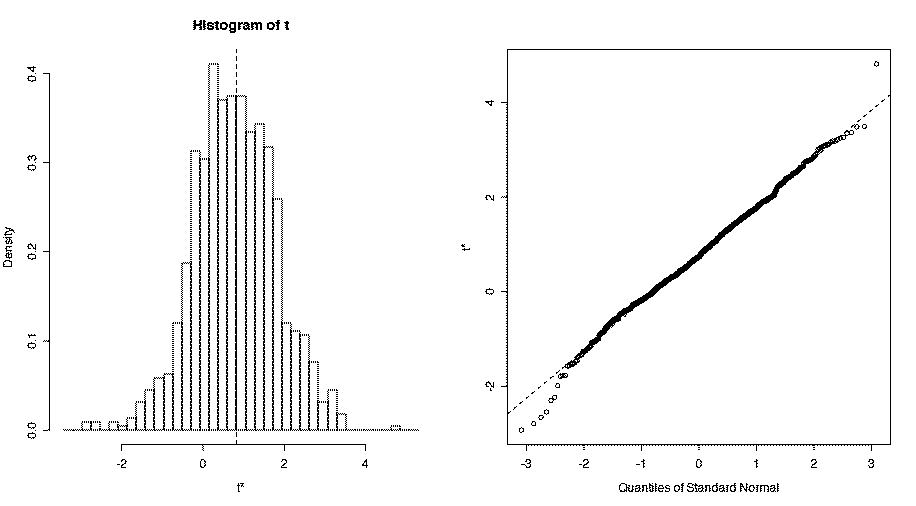
plot(phiphi.boot)

# Evaluation de p_star

p_star <- 1/B * sum((phiphi.boot$t > s))
print(p_star)
[1] 0.48

On observe ici p*=0.48, et on conclut donc sur H0 (comme pour le test paramétrique classique). La distribution des valeurs s* est donnée par :

5.2 Test de comparaison de deux moyennes sur des groupes indépendants

Méthode indiquée par Rapacchi.

La différence des moyennes observées sur les échantillons est t. on construit B échantillons bootstrap à partir de chacun des deux échantillons observés. Pour chacun des échantillons bootstrap, on calcule la différence des moyennes t_b*. Enfin, on calcule la moyenne de ces différences et leur erreur standard s*. On conclut à partir de la valeur du rapport t/s* (par référence à une loi normale ?).

# L'exemple des souris : temps de survie de deux echantillons de souris de laboratoire.
# Un groupe "traite" et un groupe "controle"

traite <- c(94, 197, 16, 38, 99, 141, 23)
controle <- c(52, 104, 146, 10, 51, 30, 40, 27, 46)

# Tests classiques :
print("Test de Student")
print(t.test(traite, controle))
# Welch Two Sample t-test
# data: traite and controle
# t = 1.0587, df = 9.654, p-value = 0.3155
# alternative hypothesis: true difference in means is not equal to 0
# 95 percent confidence interval:
# -34.15279 95.42263
# sample estimates:
# mean of x mean of y
# 86.85714 56.22222

print("Test de Wilcoxon Mann Whitney")
print(wilcox.test(traite,controle))
# Wilcoxon rank sum test
# data: traite and controle
# W = 36, p-value = 0.6806
# alternative hypothesis: true location shift is not equal to 0

# Test bootstrap. Premiere methode

t <- mean(traite) - mean(controle)

moyenne <- function(d,w) {
n <- length(d)
ech <- c(d[w[1:n]])
return(mean(ech))
}

# Nombre de bootstraps :

B <- 1000

traite.boot <- boot(traite, statistic=moyenne, R=B)
controle.boot <- boot(controle, statistic=moyenne, R=B)

s_star <- sd(traite.boot$t - controle.boot$t)

effet <- t/s_star
print(effet)
# [1] 1.129217

La valeur trouvée est trop faible pour conclure à un effet.

Méthode indiquée par Marazzi :

On calcule la statistique classique du t-test : (différence des moyennes d'échantillons)/racine(somme des carrés des erreurs types) à partir des échantillons observés. Soit s la valeur trouvée. On construit ensuite les "échantillons déplacés" en considérant les écarts à la moyenne dans chacun des deux échantillons. On tire B échantillons par bootsrap à partir de chacun des deux échantillons déplacés, et on évalue pour b=1, 2, ..., B, la statistique s_b*. Enfin, on calcule la p-value bootstrap :

p* = 1/B (Nombre de s_b* > s)

et on rejette H0 si p* < a/2 ou p* > 1 - a/2.

Sur l'exemple traité précédemment, cette méthode conduit aux résultats suivants :

# Test Bootstrap. Deuxième méthode
s <- (mean(traite)-mean(controle))/sqrt(var(traite)/length(traite)+var(controle)/length(controle))
print("Valeur de s :")
print(s)
ecart.traite <- traite - mean(traite)
ecart.controle <- controle - mean(controle)

strates <- c(rep(1,length(traite)),rep(2,length(controle)))

moyennes <- function(d,w, str=str) {
n1 <- sum((str==1))
n2 <- sum((str==2))
m <- n1 + 1
n <- n1 + n2

ech1 <- c(d[w[1:n1]])
ech2 <- c(d[w[m:n]])
return((mean(ech1)-mean(ech2))/sqrt(var(ech1)/n1+var(ech2)/n2))
}

B <- 1000

comp.moyennes.boot <-boot(c(ecart.traite,ecart.controle), statistic=moyennes,R=B, strata=strates, str=strates )

plot(comp.moyennes.boot)

# Evaluation de p_star

p_star <- 1/B * sum((comp.moyennes.boot$t > s))
print("Valeur de p_star")
print(p_star)
[1] 0.135

De nouveau, la valeur trouvée n'est pas significative. La distribution des valeurs t_b* peut être représentée graphiquement de la manière suivante :

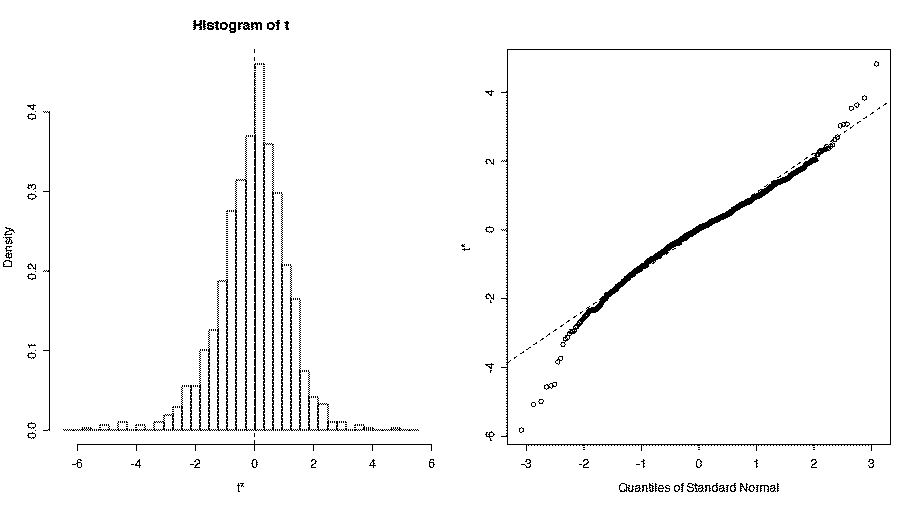
Remarque. On utilise ici une possibilité offerte par la fonction boot(), qui permet d'introduire des échantillons stratifiés.

5.3 Test l'identité de deux distributions

Etant donné deux échantillons indépendants, de tailles respectives m et n, est-il légitime de supposer que la variable suit la même loi dans les deux populations d'où sont issus les échantillons? La statistique utilisée est la même que dans le cas précédent. En revanche, le ré-échantillonnage est réalisé de la manière suivante:

- On calcule la statistique s à partir des échantillons de départ

- On tire B échantillons bootstrap dans la réunion des deux échantillons de départ.

- A partir chaque échantillon bootstrap de taille m+n, on forme un échantillon de taille m en considérant les m premières valeurs, et un échantillon de taille n en considérant les n dernières. On calcule la statistique s_b* à partir de ces deux échantillons.

- Comme précédemment, on calcule la p-value bootstrap par :

p* = 1/B (Nombre de s_b* > s)

et on rejette H0 si p* < a/2 ou p* > 1 - a/2.

Exemple des souris :

traite <- c(94, 197, 16, 38, 99, 141, 23)
controle <- c(52, 104, 146, 10, 51, 30, 40, 27, 46)

# Test classique :
print("Test de Kolmogorov et Smirnov")
[1] "Test de Kolmogorov et Smirnov"
print(ks.test(traite, controle))

Two-sample Kolmogorov-Smirnov test

data: traite and controle
D = 0.3492, p-value = 0.6119
alternative hypothesis: two-sided

# Test bootstrap de comparaison des distributions

s <- (mean(traite)-mean(controle))/sqrt(var(traite)/length(traite)+var(controle)/length(controle))
print("Valeur de s :")
[1] "Valeur de s :"
print(s)
[1] 1.058711

moyennes <- function(d,w, n1, n2) {
m <- n1 + 1
n <- n1 + n2
ech1 <- c(d[w[1:n1]])
ech2 <- c(d[w[m:n]])
return((mean(ech1)-mean(ech2))/sqrt(var(ech1)/n1+var(ech2)/n2))
}

B <- 1000
comp.dist.boot <-boot(c(traite,controle), statistic=moyennes,R=B, n1=length(traite), n2=length(controle) )
plot(comp.dist.boot)
# Evaluation de p_star
p_star <- 1/B * sum((comp.dist.boot$t > s))
print("Valeur de p_star")
[1] "Valeur de p_star"
print(p_star)
[1] 0.154

5.4 Autre exemple

In a study of correlates of authoritarian personality structure, one hypothesis was that people high in authoritarianism would show a greater tendency to possess stereotypes about members of various national and ethnic groups than would those low in authoritarianism. This hypothesis was tested with a group of 98 randomly selected college women. Each subject was given 20 photographs and asked to "identify" (by matching) as many or as few photographs as they wished. Since, unknown to the subjects, all photographs were of Mexican nationals { either candidates for the Mexican legislature or winners in a Mexican beauty contest and since the matching list of 20 different national and ethnic groups did not include "Mexican", the number of photographs which any subject identified constitutes an index of that subject's tendency to stereotype. Authoritarianism was measured by the F scale of authoritarianism, and the subjects were
grouped as "high" and "low" scorers. High scorers were those who scored at or above the median on the F scale ; low scorers were those who scored below the median. The prediction was that these two groups would differ in the number of photographs they identified.

N.B. Situation proposée par Siegel et Castellan. Valeurs légèrement modifiées.

Low <- c(rep(1,11), rep(4, 7), rep(7,8), rep(10,3), rep(13,5), rep(16,5), rep(19,5))
High <- c(rep(1,3), rep(4, 3), rep(7,8), rep(10,12), rep(13,12), rep(16,12), rep(19,4))

> Low
[1] 1 1 1 1 1 1 1 1 1 1 1 4 4 4 4 4 4 4 7 7 7 7 7 7 7 7 10 10 10 13 13 13 13 13 16
[36] 16 16 16 16 19 19 19 19 19
> High
[1] 1 1 1 4 4 4 7 7 7 7 7 7 7 7 10 10 10 10 10 10 10 10 10 10 10 10 13 13 13 13 13 13 13 13 13
[36] 13 13 13 16 16 16 16 16 16 16 16 16 16 16 16 19 19 19 19

Comparaison de moyennes

[1] "Test de Student"

Welch Two Sample t-test

data: Low and High
t = -2.6916, df = 77.962, p-value = 0.008699
alternative hypothesis: true difference in means is not equal to 0
95 percent confidence interval:
-5.3815219 -0.8053468
sample estimates:
mean of x mean of y
8.295455 11.388889

[1] "Test de Wilcoxon Mann Whitney"

Wilcoxon rank sum test with continuity correction

data: Low and High
W = 828, p-value = 0.009382
alternative hypothesis: true location shift is not equal to 0

Test bootstrap - première méthode

[1] "Effet"
[1] -2.620323

D'où un effet significatif

Test bootstrap de comparaison de moyennes - deuxième méthode

[1] "Valeur de s :"
[1] -2.691594
[1] "Valeur de p_star"
[1] 0.992
Warning message:

Test bootstrap de comparaison des distributions

# Test classiques :
print("Test de Kolmogorov et Smirnov")
print(ks.test(Low, High))

# Test bootstrap de comparaison des distributions

s <- (mean(Low)-mean(High))/sqrt(var(Low)/length(Low)+var(High)/length(High))
print("Valeur de s :")
print(s)

[1] "Valeur de s :"
[1] -2.691594

moyennes <- function(d,w, n1, n2) {
m <- n1 + 1
n <- n1 + n2
ech1 <- c(d[w[1:n1]])
ech2 <- c(d[w[m:n]])
return((mean(ech1)-mean(ech2))/sqrt(var(ech1)/n1+var(ech2)/n2))
}

B <- 1000

comp.dist.boot <-boot(c(Low,High), statistic=moyennes,R=B, n1=length(Low), n2=length(High) )

plot(comp.dist.boot)

# Evaluation de p_star

p_star <- 1/B * sum((comp.dist.boot$t > s))
print("Valeur de p_star")
print(p_star)

[1] "Valeur de p_star"
[1] 0.997