Analyse factorielle des correspondances avec R

Plusieurs packages fournissent des outils permettant de réaliser une analyse factorielle des correspondances. On peut citer :

- dans le package MASS : mva

- dans le package ade4 : dudi.acm

- dans le package FactoMineR (cf. http://factominer.free.fr) : MCA

Les résultats les plus complets semblent être ceux fournis par la procédure MCA.

Exemple :

Reprenons l'exemple "Les étudiants et la ville" déjà décrit dans les exemples traités sous Statistica.

Présentation des données :

Réf.  Il s'agit d'une partie des données issues de l'enquête "Les étudiants et la ville" effectuée en 2001 par des étudiants de sociologie sous la direction de S. Denèfle à l'Université de Tours. Cet exemple est décrit dans : Crucianu M., Asselin de Beauville J-P., Boné R., Méthodes factorielles pour l'analyse des données, Hermès-Lavoisier 2004.

L'analyse porte sur cinq questions en rapport avec le logement étudiant. L'ensemble des  individus statistiques est ici un échantillon de 383 étudiants. Les questions sont les suivantes : 

Pour l'ACM, il est quasiment indispensable de regrouper les modalités dont la fréquence est trop faible (inférieure à 5% par exemple) avec d'autres modalités. Aussi, dans les données qui suivent, les modalités "Parents" et "NR1" ont été regroupées pour la variable "mode", de même que "NA" et "NR3" pour la variable "ancienneté" et ">5km" et "NR4" pour la variable "éloignement". Il reste donc 22 modalités distinctes.

 Les données recueillies peuvent être représentées, de façon classique, à l'aide d'un tableau protocole ou d'un tableau d'effectifs. Cependant, deux autres représentations sont également utilisées : le tableau disjonctif complet (TDC) et le tableau de Burt (TdB). Ici, les données sur lesquelles nous allons travailler est un tableau protocole fictif, généré artificiellement à partir du tableau de Burt indiqué par l'auteur.

Ce tableau peut être téléchargé au format .csv ou au format .Rdata.

Chargement des données :

A partir du fichier enregistré au format .csv

etudiants.proto <- read.csv2(file.choose()) # Choisir le fichier Etudiants-ville-protocole.csv

A partir du fichier enregistré au format .Rdata

load(file.choose()) # Choisir le fichier Etudiants-Ville-protocole.RData

Visualiser les données :

> etudiants.proto
Mode Type Ancien Eloign Superf
1 Par_NR Autre NA_NR plus_5km_NR plus_30m
2 Par_NR Autre NA_NR de_1_5km NR5
3 Par_NR Autre NA_NR plus_5km_NR NR5
4 Par_NR Autre NA_NR plus_5km_NR NR5
5 Par_NR Autre NA_NR plus_5km_NR NR5
...
378 Par_NR NR2 NA_NR de_1_5km NR5
379 Seul Appart NA_NR plus_5km_NR de_10_20m
380 Couple Autre de_1_3ans de_1_5km plus_30m
381 Seul NR2 plus_3ans plus_5km_NR moins_10m
382 Coloc NR2 moins_1an de_1_5km plus_30m
383 Par_NR Autre de_1_3ans plus_5km_NR NR5

Produire les principaux résultats de l'AFC :

La commande étudiée ici (MCA du package FactoMiner) s'applique au tableau protocole. On peut noter que cette commande permet aussi de spécifier des individus et des variables supplémentaires. Pour réaliser une ACM à partir du tableau disjonctif complet ou du tableau de Burt, il faut utiliser les commandes relatives à l'analyse factorielle des correspondances.

Réaliser l'AFC en extrayant 3 facteurs :

library(FactoMineR)
etudiants.MCA <- MCA(etudiants.proto, ncp=3)
options(digits=3)
summary(etudiants.MCA)
Length Class Mode
eig 3 data.frame list
call 5 -none- list
ind 3 -none- list
var 4 -none- list
svd 3 -none- list

Les valeurs propres et l'inertie de chaque axe

etudiants.MCA$eig
eigenvalue inertia cumulative inertia
dim 1 7.22e-01 2.12e+01 21.2
dim 2 4.03e-01 1.19e+01 33.1
dim 3 3.29e-01 9.67e+00 42.8
dim 4 2.52e-01 7.41e+00 50.2
dim 5 2.36e-01 6.94e+00 57.1
dim 6 2.10e-01 6.19e+00 63.3
dim 7 1.98e-01 5.84e+00 69.1
dim 8 1.86e-01 5.48e+00 74.6
dim 9 1.71e-01 5.02e+00 79.6
dim 10 1.67e-01 4.90e+00 84.6
dim 11 1.24e-01 3.65e+00 88.2
dim 12 1.10e-01 3.25e+00 91.4
dim 13 1.04e-01 3.07e+00 94.5
dim 14 7.47e-02 2.20e+00 96.7
dim 15 5.53e-02 1.63e+00 98.3
dim 16 3.85e-02 1.13e+00 99.5
dim 17 1.82e-02 5.35e-01 100.0
dim 18 3.92e-30 1.15e-28 100.0
dim 19 1.20e-30 3.52e-29 100.0
dim 20 1.30e-31 3.83e-30 100.0
dim 21 3.10e-32 9.13e-31 100.0
dim 22 5.65e-33 1.66e-31 100.0

Les paramètres d'appel : tableau protocole, marges ligne et colonne, nombre de facteurs

etudiants.MCA$call
$X
Mode Type Ancien Eloign Superf
1 Par_NR Autre NA_NR plus_5km_NR plus_30m
2 Par_NR Autre NA_NR de_1_5km NR5

$marge.col
Coloc Couple Par_NR Seul Appart ...
0.0277 0.0261 0.0496 0.0966 0.0606 0.0397 ...

$marge.row
1 2 3 4 5 6 7 8 9...
0.00261 0.00261 0.00261 0.00261 0.00261 0.00261 0.00261 0.00261 0.00261 ...

$ncp
[1] 3

$quali
[1] 1 2 3 4 5

Résultats relatifs aux individus : coordonnées, contributions, qualités de représentation

etudiants.MCA$ind
$coord
Dim 1 Dim 2 Dim 3
1 1.493799 -0.007911 0.04935
2 1.529649 0.425435 -0.17849

$contrib
Dim 1 Dim 2 Dim 3
1 8.07e-01 4.05e-05 1.93e-03
2 8.47e-01 1.17e-01 2.53e-02

$cos2
Dim 1 Dim 2 Dim 3
1 7.52e-01 2.11e-05 8.21e-04
2 5.59e-01 4.32e-02 7.61e-03

Résultats relatifs aux variables : coordonnées, contributions, qualités de représentation, valeurs test

etudiants.MCA$var
$coord
Dim 1 Dim 2 Dim 3
Coloc -0.228 -1.0201 0.7869
Couple -0.222 -1.3155 0.2448
Par_NR 1.591 0.2388 -0.0995
Seul -0.692 0.5251 -0.2405
Appart -0.239 -1.0433 0.3581
Autre 1.585 0.1322 -0.0137
Chamb -0.236 0.7976 0.0280
Cite -0.750 1.4395 1.9098
NR2 0.921 0.8725 -0.3942
Studio -0.718 0.1556 -1.0249
NA_NR 1.539 0.2579 -0.0823
de_1_3ans -0.474 -0.0604 0.1251
moins_1an -0.657 0.5958 0.1375
plus_3ans -0.484 -0.6110 -0.1348
de_1_5km -0.213 -0.0935 0.1793
moins_1km -0.652 0.0477 -0.2336
plus_5km_NR 1.212 0.1454 -0.1143
NR5 1.994 0.8154 -0.4956
de_10_20m -0.612 0.7532 -0.5435
de_20_30m -0.669 -0.1651 -0.8958
moins_10m -0.776 1.5959 2.0488
plus_30m 0.417 -0.7995 0.4513

$contrib
Dim 1 Dim 2 Dim 3
Coloc 0.1986 7.1407 5.21192
Couple 0.1781 11.2031 0.47600
Par_NR 17.4121 0.7017 0.14945
Seul 6.4126 6.6053 1.69934
Appart 0.4797 16.3490 2.36223
Autre 13.8180 0.1720 0.00226
Chamb 0.0805 1.6476 0.00248
Cite 1.6712 11.0007 23.74705
NR2 1.3498 2.1684 0.54289
Studio 4.0251 0.3388 18.01504
NA_NR 16.8063 0.8442 0.10533
de_1_3ans 1.5470 0.0448 0.23626
moins_1an 2.4994 3.6775 0.24035
plus_3ans 1.8642 5.3172 0.31750
de_1_5km 0.6266 0.2161 0.97474
moins_1km 3.1714 0.0304 0.89285
plus_5km_NR 9.4582 0.2436 0.18474
NR5 10.0698 3.0130 1.36494
de_10_20m 1.8422 4.9947 3.18980
de_20_30m 3.0763 0.3355 12.10479
moins_10m 1.5262 11.5419 23.32867
plus_30m 1.8867 12.4140 4.85137

$cos2
Dim 1 Dim 2 Dim 3
Coloc 0.00831 0.167113 9.95e-02
Couple 0.00739 0.259823 9.00e-03
Par_NR 0.83538 0.018816 3.27e-03
Seul 0.44749 0.257640 5.40e-02
Appart 0.02482 0.472894 5.57e-02
Autre 0.62191 0.004326 4.63e-05
Chamb 0.00306 0.035054 4.31e-05
Cite 0.06752 0.248415 4.37e-01
NR2 0.05166 0.046389 9.47e-03
Studio 0.20224 0.009514 4.13e-01
NA_NR 0.81480 0.022877 2.33e-03
de_1_3ans 0.07422 0.001202 5.17e-03
moins_1an 0.11398 0.093733 5.00e-03
plus_3ans 0.09435 0.150419 7.32e-03
de_1_5km 0.04509 0.008693 3.20e-02
moins_1km 0.15650 0.000838 2.01e-02
plus_5km_NR 0.44451 0.006399 3.96e-03
NR5 0.39982 0.066866 2.47e-02
de_10_20m 0.08081 0.122457 6.38e-02
de_20_30m 0.14759 0.008996 2.65e-01
moins_10m 0.06060 0.256143 4.22e-01
plus_30m 0.11189 0.411471 1.31e-01

$vtest
Dim.1 Dim.2 Dim.3
Coloc -1.78 -7.990 6.164
Couple -1.68 -9.963 1.854
Par_NR 17.86 2.681 -1.117
Seul -13.07 9.921 -4.544
Appart -3.08 -13.440 4.613
Autre 15.41 1.285 -0.133
Chamb -1.08 3.659 0.128
Cite -5.08 9.741 12.924
NR2 4.44 4.210 -1.902
Studio -8.79 1.906 -12.553
NA_NR 17.64 2.956 -0.943
de_1_3ans -5.32 -0.678 1.405
moins_1an -6.60 5.984 1.381
plus_3ans -6.00 -7.580 -1.673
de_1_5km -4.15 -1.822 3.495
moins_1km -7.73 0.566 -2.770
plus_5km_NR 13.03 1.563 -1.229
NR5 12.36 5.054 -3.072
de_10_20m -5.56 6.839 -4.936
de_20_30m -7.51 -1.854 -10.055
moins_10m -4.81 9.892 12.699
plus_30m 6.54 -12.537 7.077

Valeurs singulières, vecteurs propres, etc

etudiants.MCA$svd
$vs
[1] 8.49e-01 6.35e-01 5.73e-01 5.02e-01 4.86e-01 4.59e-01 ...
$U
[,1] [,2] [,3] [,4] [,5] [,6]
[1,] 1.758594 -0.012458 0.08605 -0.3257 -0.8417 0.5053 ...
[2,] 1.800799 0.669924 -0.31126 -0.1818 -0.6220 -0.5983 ...
$V
[,1] [,2] [,3] [,4] [,5] [,6] [,7]
[1,] -0.268 -1.6063 1.3723 2.3295 1.0330 0.4042 -1.85550 ....
[2,] -0.261 -2.0714 0.4270 -1.8769 1.0655 -0.4382 1.98831 ....

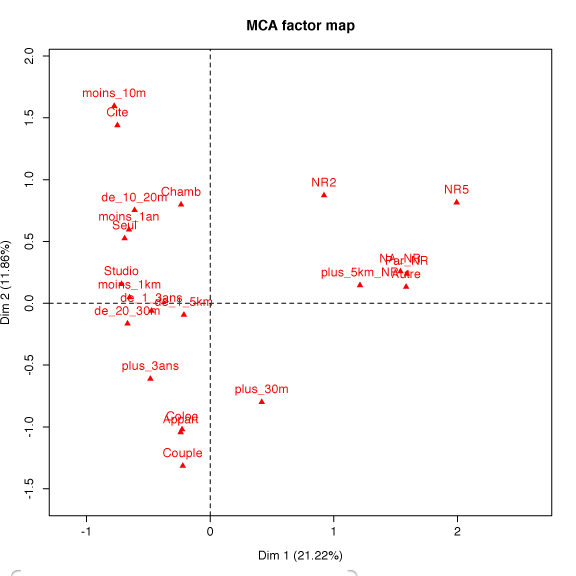
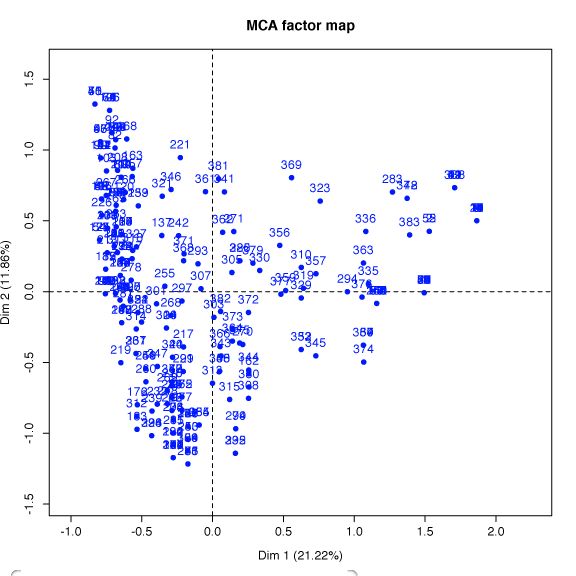
Par défaut, la procédure fournit également les représentations graphiques des individus, des variables et la représentation conjointe dans le plan (CP1, CP2). On peut également produire ces graphiques à l'aide de la commande plot.MCA. Le paramètre axes = c(x,y) permet alors d'obtenir les représentations selon d'autres axes principaux.

Quelques compléments disponibles dans le package ade4.

Le package ade4 fournit une commande permettant de générer le tableau disjonctif complet à partir du tableau protocole, et on peut assez facilement obtenir ainsi le tableau de Burt comme produit de matrices : t(X).X, où X est la matrice du tableau disjonctif complet et t() désigne la transposition des matrices.

library(ade4)
etudiants.disj <- acm.disjonctif(etudiants.proto)

etudiants.disj
Mode.Coloc Mode.Couple Mode.Par_NR Mode.Seul Type.Appart Type.Autre Type.Cham
1            0           0           1         0           0          1          0
2            0           0           1         0           0          1          0

etudiants.burt <- t(etudiants.disj) %*% as.matrix(etudiants.disj)
etudiants.burt
                   Mode.Coloc Mode.Couple Mode.Par_NR Mode.Seul Type.Appart
Mode.Coloc                 53           0           0         0          32  
Mode.Couple                 0          50           0         0          34  

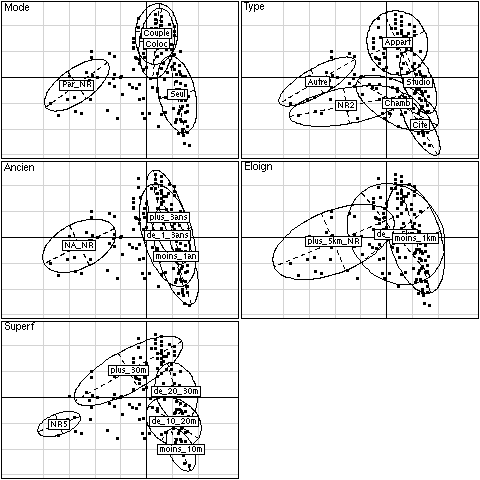
Le package ade4 fournit pour l'ACM la représentation graphique originale suivante :

library(ade4)
etudiants.acm <- dudi.acm(etudiants.proto)
Select the number of axes:
3
png("/Users/carpenti/Desktop/ACM-avec-R-Gra4.png")
scatter(etudiants.acm)
dev.off()

Page rédigée le 27 mai 2007