I study spatio-temporal stochastic processes arising in population genetics, evolutionary ecology.
I try to describe the limiting behaviour and the asymptotic fluctuations of these spatio-temporal processes in different regimes.
At the moment, my research focuses on three main aspects.
Spatial models in population genetics
During my PhD, I started to work on the spatial Lambda-Fleming-Viot process, developed by N. Barton, A. Etheridge and A. Véber.
This model describes the evolution of the genetic composition of a spatially structured population, taking into account dispersal, mutations, natural selection and the randomness of reproduction events (called genetic drift), for a population evolving in any spatial dimension.
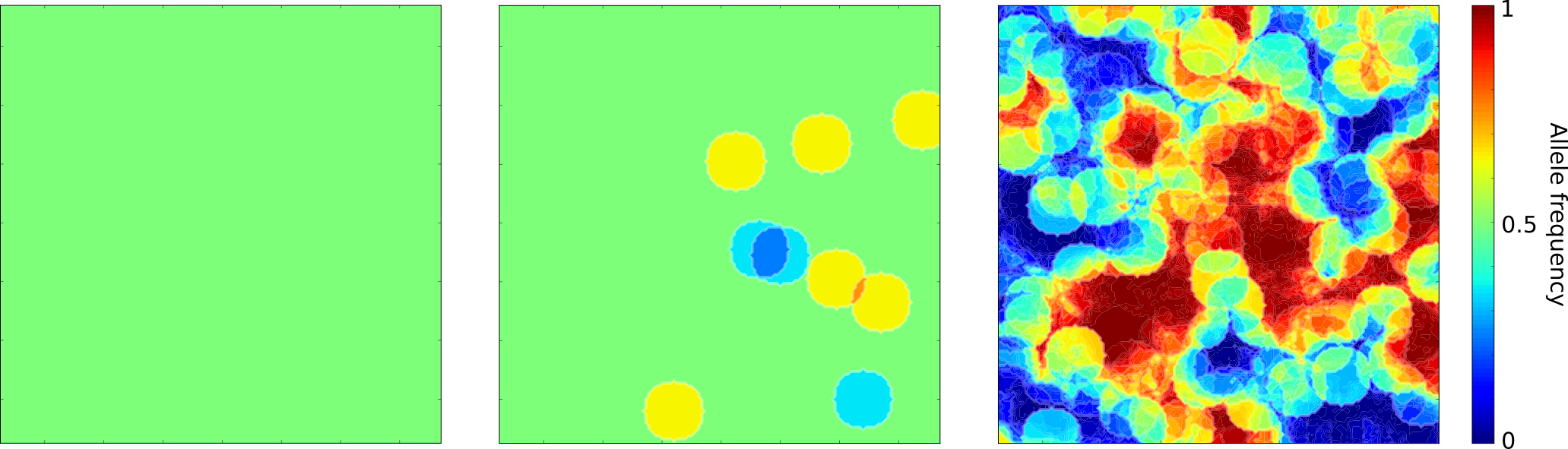
For example, the figure above shows the evolution of a single (neutral) allele frequency in a two-dimensional space, starting from a uniform 1/2 frequency.
After a few reproduction events, the frequency has increased in some regions, and decreased in others, and after many reproduction events, we see some regions where the frequency is close to 1 and other regions where it is close to 0, separated by very wiggly interfaces where the frequency is between 0 and 1.
My work focuses on finding scaling limits of this process (and of the related stepping-stone model in discrete space) in various settings: natural selection, heterogeneous dispersal, with obstacles, etc.
More recently, with Alison Etheridge and Sarah Penington, I have started to study the expansion of an allele under bistable frequency-dependent selection.
Related publications
- 'Central limit theorems describing isolation by distance under varying population size', R. F., Bastian Wiederhold, ALEA, Lat. Am. J. Probab. Math. Stat. 22:283-330, 2025 [pdf].
- 'Stochastic partial differential equations describing isolation by distance under various forms of power-law dispersal', R.F., Bastian Wiederhold, ESAIM: Probability and Statistics, 29, p.113-157, 2025 [pdf].
- 'Demographic inference for spatially heterogeneous populations using long shared haplotypes', R. F., Harald Ringbauer, Graham Coop, Theoretical Population Biology, 159, p.108-124, 2024, [pdf]
- 'Stochastic partial differential equations describing neutral genetic diversity under short range and long range dispersal', R. F., Electronic Journal of Probability, 27:1-41 (2022) [pdf].
- 'The stepping stone model in a random environment and the effect of local heterogneities on isolation by distance patterns', R.F., Electronic Journal of Probability, 24(57):1-35, 2019 [pdf]
- 'Gene flow across geographical barriers: scaling limits of random walks with obstacles', R.F., Stochastic Processes and their Applications, 129(10):3748-3773, 2019, [arxiv:1711.02589]
- 'A central limit theorem for the spatial Lambda Fleming-Viot process with selection', R. F. and Sarah Penington, Electronic Journal of Probability, 22(5):1-68 2017. [pdf].
Genealogies arising in interacting population models
An extension of my work on population genetics models is the study of genealogies arising in general population models under various assumptions.
This is especially challenging when the population size randomly fluctuates in time (and space), as already showed by B. Wiederhold's PhD work cited above.
Such models can take the form of branching processes with interactions (in which the rates of branching and dying depend on the state of the whole population), or more general models.
Related publications
- 'Lambda-Fleming-Viot processes arising in logistic Galton-Watson processes with a large carrying capacity', R. F., preprint [arxiv:2501.16837].
- 'Stochastic neutral fractions and the effective population size' R. F., Emmanuel Schertzer, Zsófia Talyigás, Julie Tourniaire, preprint [arXiv:2502.05062].
Adaptation of trait-structured populations under environmental stress
As a part of the ANR project RESISTE, coordinated by Lionel Roques and Guillaume Martin, I study stochastic and deterministic models describing the evolution of the phenotype distribution of adapting populations under environmental stress.
This stress can take the form of a moving environment, where the phenotype conferring the maximal fitness gradually moves away from its current position, or of a brutal change in the fitness landscape.
In the latter case, some populations are unable to adapt to the new environment, and become extinct, while others are able to evolve in order to survive.
This is called evolutionary rescue and is at the centre of the ANR RESISTE project.
Related publications
- 'A measure-valued stochastic model for vector-borne viruses', Mario Ayala, Jerôme Coville, R.F., ALEA, Lat. Am. J. Probab. Math. Stat. 21, 1145–1193 (2024) [pdf].
- 'The emergence of a birth-dependent mutation rate: causes and consequences', Florian Patout, R. F., Matthieu Alfaro, Julien Papaïx and Lionel Roques, preprint [arXiv:2101.01923], peer-reviewed and recommended by Peer Community in Mathematical and Computational Biology.
- 'Ancestral lineages in mutation-selection equilibria with moving optimum', Florian Patout, R. F. and Jimmy Garnier, Bull Math Biol. 84, 93 (2022) [pdf].
General epidemic models
The classical SIR epidemic model describes the evolution of the proportions of susceptible (S), infectious (I) and revmoved (R) individuals in a large population during a major epidemic.
According to this model, the proportions 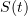 ,
, 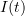 and
and 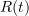 solve the following system of ordinary differential equations:
solve the following system of ordinary differential equations:
These equation describe the large population limit of a stochastic epidemic model under some crucial assumptions: the population is homogeneous, and infectious contacts take place between uniformly sampled pairs of individuals, and infected individuals remain infectious (with constant infectivity 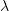 ) during i.i.d. exponentially distributed periods (with parameter
) during i.i.d. exponentially distributed periods (with parameter 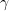 ).
In collaboration with Etienne Pardoux and Guodong Pang, I study generalisations of this model which relax one or several of these assumptions.
).
In collaboration with Etienne Pardoux and Guodong Pang, I study generalisations of this model which relax one or several of these assumptions.
In particular, we are interested in non-Markovian epidemic models, where infected individuals remain infectious during arbitrarily distributed periods, and where their infectivity is given by a random function of time of the form 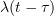 , where
, where  is the time at which the individual is infected.
The large population limit of such a system then takes the form of a system of integral equations, which are non-local in time (also called distributed delay equations).
is the time at which the individual is infected.
The large population limit of such a system then takes the form of a system of integral equations, which are non-local in time (also called distributed delay equations).
Related publications
- 'Stochastic epidemic models with varying infectivity and susceptibility', R.F., Guodong Pang, Étienne Pardoux, Arsene Brice Zotsa-Ngoufack, Annals of Applied Probability, 35(3), 2025 [arXiv:2210.04667].
- 'Multi-patch multi-group epidemic model with varying infectivity', R.F., Guodong Pang, Étienne Pardoux, Probability, Uncertainty and Quantitative Risk, 2022, 7(4): 333-364 [view on journal website].
- 'Recent advances in epidemic modeling: non-Markov stochastic models and their scaling limits', R. F., Guodong Pang, Etienne Pardoux, Graduate J. Math. 7(2), 19-75, 2022 [view on journal website].
- 'Epidemic models with varying infectivity', R. F., Guodong Pang and Etienne Pardoux, SIAM Journal on Applied Mathematics, 81(5):1893-1930, 2021 [pdf].
- 'Estimating the state of the Covid-19 epidemic in France using a model with memory', R. F., Guodong Pang and Etienne Pardoux, 2021, R. Soc. open sci. 8:202327. [https://doi.org/10.1098/rsos.202327].
- 'Household epidemic models and McKean-Vlasov Poisson driven SDEs', R. F. and Étienne Pardoux, Annals of Applied Probability, 32(2):1210-1233 (2022) [arXiv:1907.03001].


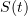 ,
, 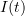 and
and 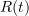 solve the following system of ordinary differential equations:
solve the following system of ordinary differential equations: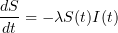
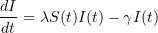
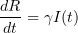
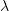 ) during i.i.d. exponentially distributed periods (with parameter
) during i.i.d. exponentially distributed periods (with parameter 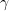 ).
In collaboration with
).
In collaboration with 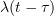 , where
, where  is the time at which the individual is infected.
The large population limit of such a system then takes the form of a system of integral equations, which are non-local in time (also called distributed delay equations).
is the time at which the individual is infected.
The large population limit of such a system then takes the form of a system of integral equations, which are non-local in time (also called distributed delay equations).