Characterization of Generalized Coherent States through Intensity-Field Correlations

Created on January 01, 2026

2026   ·   BbQExpat   NonGaussianStates   Nonclassicality   QuantumOptics

image Related Publication
Ignacio Salinas Valdivieso, Victor Gondret, Gerd Hartmann Salvo, Mariano Uria, Pablo Solano and Carla Hermann-Avigliano, Characterization of Generalized Coherent States through Intensity-Field Correlations, arXiv, 2512.15655.

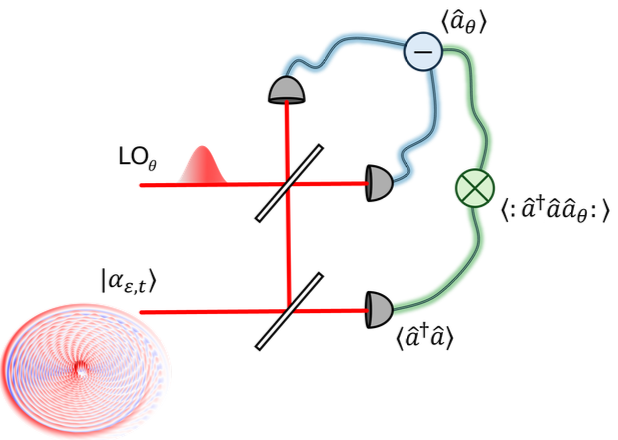
Homodyne Detection scheme
FIG 1: homodyne detection scheme with a phase θ between the state and the local oscillator (LO).

Generalized coherent states (GCSs) [1] is a family of quantum states which remain coherent to any order in the sens of Glauber [2]. This means that their normalized n-body correlation function is equal to 1 for any value of n. However, these states do exhibit interesting quantum features such as negativity and metrological advantages [3]. Because of their coherence nature, their nonclassical properties cannot be revealed through standard intensity-intensity correlation measurements. In this work, we have demonstrated that the intensity-field correlation function [4] alone provides a witness of nonclassicality for GCSs. The main advantage of this witness lies in its experimental simplicity: the state is split in two, one part goes in an intensity detector and the other part is sent to the field detector, which consists in a balanced homodyne detection scheme along a phase θ. We then simply compute the equal time correlation function between the quadrature with phase θ and the intensity measurement. If the normalized correlation function differs from 1, the state is nonclassical in the sense that its Glauber-Sudarshan P-distribution is ill-defined. This simple witness is a consequence of the two-body body coherence of the state [5].

In addition, we derive analytical results for Kerr-generated states and extend the analysis to statistical mixtures of GCSs. The proposed approach enables real-time, low-complexity detection of quantum signatures in non-Gaussian states, offering a practical tool for experiments across a broad range of nonlinear regimes.

Bibliography

[1] D. Stoler, “Generalized Coherent States”, Physical Review D 4,2309–2312 (1971).

[2] R. J. Glauber, “Coherent and Incoherent States of the Radiation Field”, Physical Review 131,2766–2788 (1963).

[3] M. Uria, A. Maldonado-Trapp, C. Hermann-Avigliano, and P. Solano, “Emergence of non-Gaussian coherent states through nonlinear interactions”, Physical Review Research 5, 013165 (2023)

[4] H. J. Carmichael, H. M. Castro-Beltran, G. T. Foster, and L. A. Orozco, “Giant Violations of Classical Inequalities through Conditional Homodyne Detection of the Quadrature Amplitudes of Light”, Physical Review Letters 85, 1855–1858 (2000)

[5] E. V. Shchukin and W.Vogel,“Nonclassical moments and their measurement”, Physical Review A 72, 043808(2005).