MDS classique avec R

En Français : échelles multidimensionnelles, positionnement multidimensionnel

Source : Borg, I., Groenen, P., Modern Multidimensional Scaling : Theory and Applications, Second Edition, Springer, 2005.

Principe de la méthode :

On désigne sous le terme de MDS (multidimensional scaling), un ensemble de techniques permettant de représenter les données d'une matrice de proximités entre objets à l'aide de modèles de distances spatiales. Dans sa version la plus simple, la méthode MDS permet de retrouver une carte bi-dimensionnelle à partir d'un ensemble de distances mutuelles entre lieux.

Le MDS classique est une méthode est fondée sur les travaux de Torgerson (1952, 1958) et Gower. Elle est appelée Classical MDS, AFTD (analyse factorielle sur un tableau de distances), Principal Coordinates Analysis, ou encore Analyse du triple (Benzécri).

Principe mathématique : on calcule les valeurs propres et vecteurs propres d'une matrice calculée à partie de la matrice de proximités, afin de déterminer la "meilleure" projection de l'ensemble d'objets dans un sous-espace de dimension donnée.

Algorithme :

On dispose au départ de la matrice n x n des "distances" mutuelles entre n objets. On souhaite obtenir une représentation de ces n objets dans un espace de dimension m en respectant "au mieux" les distances entre les objets. La dimension m de l'espace n'est pas fixée a priori.

• On part d'une matrice n x n de distances mutuelles entre objets : P
• On calcule P2, matrice n x n des carrés des distances précédentes
• On effectue une opération de double centrage : B = -0.5 * J * P2 *J
  où J = In - 1/n 1n, In est la matrice unité d'ordre n, 1n est la matrice n x n dont tous les coefficients sont égaux à 1.
• On calcule les valeurs propres et vecteurs propres (unitaires) de la matrice B. On conserve les m plus grandes valeurs propres. Soit Lm la matrice diagonale de ces m valeurs propres, et Em la matrice des vecteurs propres unitaires correspondants. Soit Lm^.5 la matrice des racines carrées de ces valeurs propres.
• X = Em * Lm^.5 fournit une solution du problème posé. Les coordonnées des n points dans l'espace de dimension n sont les lignes de la matrice solution X (matrice à n lignes et m colonnes).

Remarque :

Si la matrice P de départ est une matrice de distances euclidiennes, le MDS classique fournit en résultat les coordonnées des n points, à une rotation près, dans un repère dont l'origine est le centre de gravité des points.

Propriété de minimalité de la solution :

On montre que la solution trouvée minimise la fonction de perte (appelée Strain, littéralement Contrainte, par Carrol et Chang) :

où X représente la matrice d'un système de n points (les variables) dans un espace de dimension n et ou la norme utilisée pour la matrice est la norme de Fröbenius, c'est-à-dire la racine carrée de la somme des carrés de tous les coefficients de la matrice. C'est en ce sens que la solution trouvée respecte "au mieux" les proximités entre objets. En particulier, si la matrice de départ est une matrice de distances euclidiennes, on obtient : Strain = 0.

Variante :

On fixe a priori le nombre m de valeurs propres à garder. On conserve alors les m plus grandes valeurs propres où les valeurs propres strictement positives, si ces dernières sont en nombre inférieur à m. Une propriété intéressante du MDS classique est que les dimensions sont emboîtées. Ainsi les deux premières dimensions d'une solution avec m=3 sont les mêmes que celles d'une solution avec m=2. Cette propriété ne se retrouve pas pour le MDS métrique (visant à minimiser le Stress).

La solution trouvée déforme alors "au minimum" les distances entre objets, tout en respectant la contrainte sur la dimension de l'espace des solutions.

Remarque.

Si P est une matrice de distances, le MDS métrique tel qu'il est décrit ici est équivalent à l'ACP avec une métrique M=I, comme on peut s'en rendre compte sur l'exemple "notes d'élèves" (cf exemple 2).

Exemple 1 :

Enoncé :

Source : Handbook of Statistics - Elsevier 2007

On se donne les distances à vol d'oiseau entre 10 villes américaines.
Les données se présentent sous la forme suivante :

Ces données sont enregistrées au format .csv d'Excel dans le fichier : FlyingMileage.csv avec la structure indiquée ci-dessus.

On peut les charger dans R à l'aide de la commande :

> distances <- read.csv2("FlyingMileage.csv")

N.B. read.csv2 permet de lire des données au format "table", avec les spécifications par défaut suivantes : séparateur = ";", séparateur décimal = ",".

Calcul des coordonnées de la représentation

On utilise la commande cmdscale, qui se trouve dans le package MASS.

> library(MASS)

> cmdscale(distances[,2:11])
[,1] [,2]
Atl -718.7594 142.99427
Chi -382.0558 -340.83962
Den 481.6023 -25.28504
Hou -161.4663 572.76991
LA 1203.7380 390.10029
Mia -1133.5271 581.90731
NY -1072.2357 -519.02423
SF 1420.6033 112.58920
Sea 1341.7225 -579.73928
DC -979.6220 -335.47281

Représentation graphique

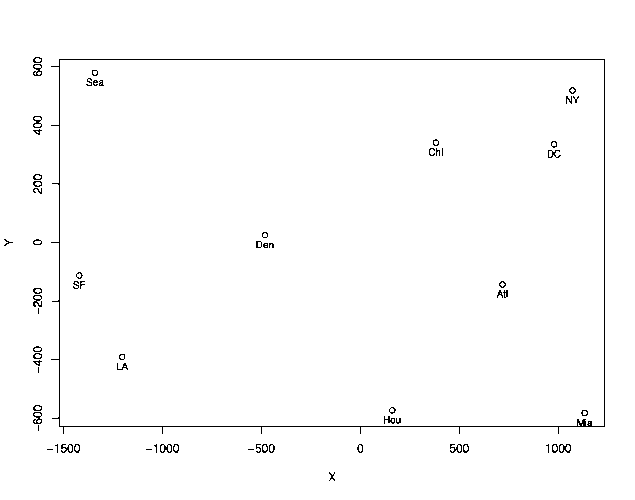
On voit que l'orientation des axes est à l'opposé des conventions utilisées pour les cartes de géographie.

On prend donc les opposés des coordonnées sur les deux axes :

> Y <- - cmdscale(distances[,2:11])[,2]
> X <- - cmdscale(distances[,2:11])[,1]

On trace ensuite le graphique et les étiquettes des points :

> plot(X,Y,type="p")
> text(X,Y,distances[,1],pos=1,cex=0.8)

Résultat obtenu :

Variantes et compléments :

On peut choisir la dimension de l'espace dans lequel le résultat est recherché.

Pour une solution en dimension 3 :

> cmdscale(distances[,2:11],k=3)

Exemple 2 :

On se donne les notes de 9 sujets dans 5 matières. Les données, après centrage et réduction, sont les suivantes (cf fichier Mini-ACP.csv):