Source : Borg, I., Groenen, P., Modern Multidimensional Scaling : Theory and Applications, Second Edition, Springer, 2005.
On désigne sous le terme de MDS (multidimensional scaling), un ensemble de techniques permettant de représenter les données d'une matrice de proximités entre objets à l'aide de modèles de distances spatiales.
Cette méthode est fondée sur les travaux de Shepard et Kruskal.
Les données sont constituées par une matrice de proximités (pij) entre n objets. Ces proximités sont soit des similarités (score élevé entre deux objets très semblables) soit des dissimilarités (score faible sur des objets très semblables). Nous supposerons dans la suite qu'il s'agit ici de dissimilarités.
On cherche une transformation monotone f(pij) sur les proximités et un système X de n points dans un espace de dimension m choisie a priori, de façon à minimiser le stress brut :
Stress =somme((f(pij)-dij)^2)
où les dij représentent les distances euclidiennes entre les points de X et la somme étendue à tous les couples i, j tels que i < j.
N.B. Des pondérations wij, dichotomiques (0 ou 1) sont parfois ajoutées dans cette formule pour tenir compte des valeurs manquantes.
Dans le MDS non métrique, on cherche à préserver l'ordre des proximités et non leurs valeurs absolues ou relatives. Autrement dit, le but est de représenter les distances entre les objets, en respectant l'ordre entre les proximités plutôt que leurs valeurs exactes. A partir des proximités pij, on détermine donc des disparités f(pij), vérifiant une règle de monotonie : si p1 < p2 alors f(p1) <= f(p2).
N.B. Contrairement à ce que les notations pourraient laisser penser, f(pij) n'est pas une fonction de p, mais une fonction de (i, j) : à deux proximités égales, mais provenant d'objets différents, peuvent correspondre des disparités différentes.
On détermine ensuite les coordonnées des points représentatifs dans l'espace image et les distances dij entre ces points, selon une méthode proche de celle utilisée en MDS métrique.
A la suite de cette étape, de nouvelles disparités sont calculées et une nouvelle solution est recherchée dans l'espace image.
On peut donc décrire très brièvement l'algorithme de la manière suivante :
Les disparités peuvent être calculées par régression monotone (Kruskal, 1964) :
Une autre méthode a été proposée par Lingoes et De Leeuw (programme MINISSA) : les rank-images ou images des rangs ou permutaton de l'image du rang (terme utilisé dans l'aide de Statistica). Dans ce cas, à partir d'une solution dij(X), on effectue une permutation entre ces points de manière que les dij(X) et les proximités pij de départ soient classées dans le même ordre.
Mais l'algorithme ainsi obtenu n'est pas nécessairement convergent et d'autres algorithmes, combinant la régression monotone et les rank-images ont été proposés. Guttman, par exemple, distingue les d-hat (obtenus par régression monotone) et les d-star (obtenus par rank-images). C'est un algorithme de ce type qui est implémenté par exemple, dans Statistica. L'aide du logiciel indique : "Les valeurs ajustées sont calculées grâce à la procédure de permutation de l'image du rang (...). Après chaque itération (..) le programme va réaliser jusqu'à cinq intérations utilisant la procédure de transformation monotone de régression."
On peut noter que la contrainte de monotonie n'indique pas de méthode particulière pour gérer les ex aequo. Plusieurs méthodes (primary approach, secondary approach, etc) ont été proposées.
On évalue la qualité de la solution trouvée à l'aide du stress (plus exactement, stress-1, car plusieurs versions de cette fonction existent dans la littérature) :
STRESS = (( somme(f(pij) - dij)^2)/somme(dij^2))^0.5
Selon Kruskal, la qualité de l'ajustement (GOF : goodness of fit) peut être évaluée de la la façon suivante :
Un autre coefficient utile est le coefficient d'aliénation qui, lui, fait intervenir les proximités de départ :
K= Racine(1 - (Somme(dij*pij)^2)/(Somme(pij^2))
Une représentation graphique utile est le diagramme de Shepard, construit en plaçant les proximités pij en abscisses, les disparités d-hat(i, j)=f(pij) et les distances dij en ordonnées et en joignant les points (pij, d-hat(i,j)) par une "ligne de régression".
Enoncé :
Source : WICKELMAIER Florian, An Introduction to MDS, Sound Quality Research Unit, Aalborg University, Denmark
On demande à des sujets d'évaluer la similitude entre 12 sons de l'environnement courant.
Les données se présentent sous la forme suivante :
| Sound |
cs
|
dd
|
fa
|
ho
|
hw
|
sh
|
st
|
sw
|
tw
|
tg
|
wa
|
wf
|
|
| circular-saw |
cs
|
0
|
1
|
4
|
5
|
3
|
4
|
2
|
8
|
8
|
5
|
7
|
1
|
| dentist-s-drill |
dd
|
1
|
0
|
3
|
8
|
2
|
6
|
2
|
7
|
8
|
8
|
7
|
2
|
| fan |
fa
|
4
|
3
|
0
|
7
|
2
|
3
|
3
|
7
|
8
|
6
|
4
|
3
|
| hooves |
ho
|
5
|
8
|
7
|
0
|
8
|
9
|
3
|
8
|
2
|
2
|
9
|
5
|
| howling-wind |
hw
|
3
|
2
|
2
|
8
|
0
|
6
|
4
|
8
|
9
|
6
|
4
|
2
|
| ship-s-horn |
sh
|
4
|
6
|
3
|
9
|
6
|
0
|
1
|
3
|
9
|
8
|
5
|
3
|
| stadium |
st
|
2
|
2
|
3
|
3
|
4
|
1
|
0
|
4
|
3
|
6
|
7
|
1
|
| stone-in-well |
sw
|
8
|
7
|
7
|
8
|
8
|
3
|
4
|
0
|
9
|
6
|
9
|
5
|
| typewriter |
tw
|
8
|
8
|
8
|
2
|
9
|
9
|
3
|
9
|
0
|
4
|
9
|
9
|
| tire-on-gravel |
tg
|
5
|
8
|
6
|
2
|
6
|
8
|
6
|
6
|
4
|
0
|
4
|
3
|
| wasp |
wa
|
7
|
7
|
4
|
9
|
4
|
5
|
7
|
9
|
9
|
4
|
0
|
6
|
| waterfall |
wf
|
1
|
2
|
3
|
5
|
2
|
3
|
1
|
5
|
9
|
3
|
6
|
0
|
Ces données sont enregistrées au format .csv d'Excel dans le fichier Sounds.csv avec la structure indiquée ci-dessus.
On peut les charger dans R à l'aide de la commande :
> proxim <- read.csv2("Sounds.csv")
N.B. read.csv2 permet de lire des données au format "table", avec les spécifications par défaut suivantes : séparateur = ";", séparateur décimal = ",".
On se limite aux données numériques :
> prox <- proxim[,3:14]
On utilise la commande isoMDS, qui se trouve dans le package MASS pour obtenir les coordonnées de la solution et le stress associé :
> library(MASS)
> prox.mds <- isoMDS(prox,cmdscale(prox))
initial value 19.391177
iter 5 value 15.912188
iter 10 value 15.596547
final value 15.560651
converged
N.B. Dans la plupart des cas, isoMDS exige une valeur initale, qui peut être celle fournie par cmdscale (le MDS métrique).
> prox.mds$points
[,1] [,2]
cs 0.20163920 -0.15873153
dd -0.76991164 -0.57955403
fa -3.02696501 -0.21941437
ho 4.51063809 -0.02440789
hw -3.05068357 -2.04720081
sh -3.11119700 2.97728343
st 0.08889741 1.45550769
sw -0.59949642 5.55410022
tw 6.21209030 0.22113765
tg 2.94117084 -2.55909595
wa -1.74966163 -5.10156742
wf -1.64652057 0.48194302
> prox.mds$stress
[1] 15.56065
> X <- prox.mds$points[,1]
> Y <- prox.mds$points[,2]
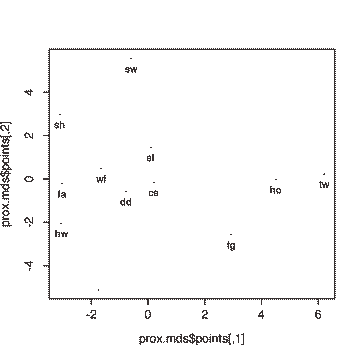
> plot(prox.mds$points, pch=".")
> text(X,Y,proxim[,2],pos=1,cex=0.8)
Résultat obtenu :

La fonction Shepard semble être assez exigeante sur la forme des paramètres qui lui sont indiqués.
On peut, par exemple, placer les données dans un "vrai" data.frame :
> prox.df <- data.frame(proxim[2:14],row.names = 1)
> prox.df
cs dd fa ho hw sh st sw tw tg wa wf
cs 0 1 4 5 3 4 2 8 8 5 7 1
dd 1 0 3 8 2 6 2 7 8 8 7 2
fa 4 3 0 7 2 3 3 7 8 6 4 3
ho 5 8 7 0 8 9 3 8 2 2 9 5
hw 3 2 2 8 0 6 4 8 9 6 4 2
sh 4 6 3 9 6 0 1 3 9 8 5 3
st 2 2 3 3 4 1 0 4 3 6 7 1
sw 8 7 7 8 8 3 4 0 9 6 9 5
tw 8 8 8 2 9 9 3 9 0 4 9 9
tg 5 8 6 2 6 8 6 6 4 0 4 3
wa 7 7 4 9 4 5 7 9 9 4 0 6
wf 1 2 3 5 2 3 1 5 9 3 6 0
On recalcule alors le positionnement multidimensionnel :
> prox.mds <- isoMDS(prox.df,cmdscale(prox.df))
initial value 19.391177
iter 5 value 15.912188
iter 10 value 15.596547
final value 15.560651
converged
Et, le premier paramètre de Shepard() doit être un objet de type dist, et non une simple matrice symétrique :
> Shepard(as.dist(prox.df),prox.mds$points)
$x
[1] 1 1 1 1 2 2 2 2 2 2 2 2 3 3 3 3 3 3 3 3 3 3 4 4 4 4 4 4 4 4 5 5 5 5
5 6 6 6 6 6 6 6 7 7 7 7 7 7 8 8 8 8 8 8 8 8 8 8 9 9 9 9 9 9 9 9
$y
[1] 1.058774 1.956057 3.543502 1.989850 1.618171 2.712178 2.208852 1.376670 1.827940 1.719079 2.981253 2.892791 3.760840
[14] 2.285605 3.197807 3.537508 1.548396 4.662825 3.598420 2.893441 6.246372 5.504074 3.229174 4.561740 5.046476 4.703821
[27] 3.319912 4.156001 4.292856 5.335548 4.311092 3.642360 6.177944 8.192778 5.179096 4.258252 6.410363 5.024849 6.013681
[40] 4.924683 8.852134 5.584463 5.314057 6.136021 4.626934 7.540125 6.263072 6.809958 5.768732 6.022443 5.309651 7.027763
[53] 4.206034 9.249553 7.827214 7.565265 7.986745 8.202600 8.191613 8.060329 9.536474 9.722141 8.650908 10.717562 9.577092
[66] 7.862937
$yf
[1] 1.058774 1.956057 2.124530 2.124530 2.124530 2.124530 2.124530
2.124530 2.124530 2.124530 2.886314 2.886314 2.886314 2.886314 2.886314
[16] 2.886314 2.886314 3.718229 3.718229 3.718229 4.529119 4.529119
4.529119 4.529119 4.529119 4.529119 4.529119 4.529119 4.529119 4.529119
[31] 4.529119 4.529119 5.772706 5.772706 5.772706 5.772706 5.772706
5.772706 5.772706 5.772706 6.102722 6.102722 6.102722 6.102722 6.102722
[46] 6.118472 6.118472 6.118472 6.118472 6.118472 6.118472 6.118472
6.118472 8.154760 8.154760 8.154760 8.154760 8.154760 8.154760 8.154760
[61] 9.303174 9.303174 9.303174 9.385864 9.385864 9.385864
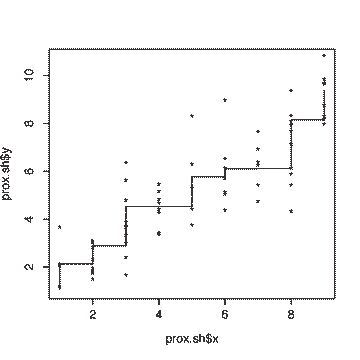
Représentation graphique du diagramme de Shepard :
> prox.sh <- Shepard(as.dist(prox.df),prox.mds$points)
> plot(prox.sh,pch="*")
> lines(prox.sh$x,prox.sh$yf,type="S")
Ce qui donne finalement :
Il s'agit d'une autre méthode de positionnement mutidimensionnel non métrique proposée par Sammon.
> sammon(prox.df)
Initial stress : 0.11654
stress after 10 iters: 0.06097, magic = 0.461
stress after 20 iters: 0.05904, magic = 0.500
stress after 30 iters: 0.05895, magic = 0.500
$points
[,1] [,2]
cs -0.8525798 -0.73382691
dd -2.0209380 -0.60379506
fa -3.5149765 -0.29830898
ho 4.3006891 -0.04742348
hw -2.7829840 -2.10319036
sh -1.5191353 2.53727622
st -0.1648869 1.28457871
sw -0.5124628 5.41515169
tw 5.3700226 1.45084191
tg 3.1379383 -1.87976686
wa -0.8867966 -5.06842641
wf -0.5538901 0.04688954
$stress
[1] 0.05895335
$call
sammon(d = prox.df)
> prox.sam <- sammon(prox.df)
> X <- prox.sam$points[,1]
> Y <- prox.sam$points[,2]
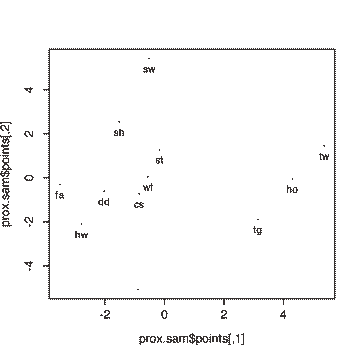
> plot(prox.sam$points,pch=".")
> text(X,Y,proxim[,2],pos=1,cex=0.8)
La représentation graphique est alors la suivante :
On peut, comme précédemment, construire un diagramme de Shepard :
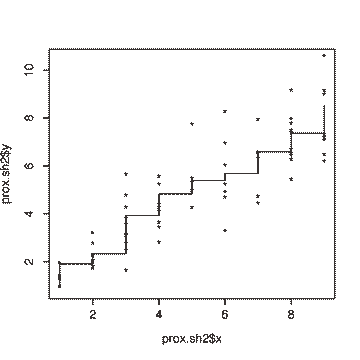
> prox.sh2 <- Shepard(as.dist(prox.df),prox.sam$points)
> plot(prox.sh2,pch="*")
> lines(prox.sh2$x,prox.sh2$yf,type="S")
Ce qui donne :