Source : Borg, I., Groenen, P., Modern Multidimensional Scaling : Theory and Applications, Second Edition, Springer, 2005.
On désigne sous le terme de MDS (multidimensional scaling), un ensemble de techniques permettant de représenter les données d'une matrice de proximités entre objets à l'aide de modèles de distances spatiales.
Parmi les auteurs qui ont travaillé sur le MDS : Shepard, Kruskal, etc.
Principe mathématique :
Les données sont constituées par une matrice de proximités (pij) entre n objets. Ces proximités sont soit des similarités (score élevé entre deux objets très semblables) soit des dissimilarités (score faible sur des objets très semblables). Les distances mesurées dans un espace métrique sont des dissimilarités particulières.
On cherche une transformation monotone f(pij) sur les proximités et un système X de n points dans un espace de dimension m choisie a priori, de façon à minimiser le stress brut :
Stress =somme((f(pij)-dij)^2)
où les dij représentent les distances euclidiennes entre les points de X et la somme étendue à tous les couples i, j tels que i < j.
N.B. Des pondérations wij, dichotomiques (0 ou 1) sont parfois ajoutées dans cette formule pour tenir compte des valeurs manquantes.
Les modèles de MDS métrique diffèrent selon le choix des transformations f admissibles :
Pour l'essentiel, il s'agit donc de trouver le minimum de la fonction Stress, fonction de m*n variables (les coordonnées des n points) à valeurs dans R+. Le calcul d'une solution est généralement fait en utilisant l'algorithme SMACOF (scaling by majorizing a convex function) (De Leeuw, 1977) ou des algorithmes du gradient (steepest descent algorithms) élaborés par Kruskal (1964) et Guttman (1968).
On évalue la qualité de la solution trouvée à l'aide du stress normalisé (plus exactement, stress-1, car plusieurs versions de cette fonction existent dans la littérature) :
STRESS = (( somme(f(p) - d)^2)/somme(d^2))^0.5
Selon Kruskal, la qualité de l'ajustement peut être évaluée de la la façon suivante :
Le diagramme construit en plaçant les proximités pij en abscisses, les disparités f(pij) et les distances dij en ordonnées est connu sous le nom de diagramme de Shepard.
MDS classique et MDS métrique
Le MDS métrique, même dans le cas du modèle Absolute MDS, diffère du MDS classique car la fonction à minimiser (Stress) est différente de celle utilisée par le MDS classique (Strain). Alors que la nature de la fonction Strain permet l'obtention d'une solution par des moyens purement algébriques (diagonalisation de matrice), les solutions du MDS métrique sont obtenues par l'application d'un algorithme itératif.
On reprend l'exemple donné pour le MDS classique : distances entre 10 grandes villes américaines.
Enoncé :
Source : Handbook of Statistics - Elsevier 2007
On se donne les distances à vol d'oiseau entre 10 villes américaines.
Les données se présentent sous la forme suivante :
| Atl | Chi | Den | Hou | LA | Mia | NY | SF | Sea | DC | |
| Atl | 0 | 587 | 1212 | 701 | 1936 | 604 | 748 | 2139 | 2182 | 543 |
| Chi | 587 | 0 | 920 | 940 | 1745 | 1188 | 713 | 1858 | 1737 | 597 |
| Den | 1212 | 920 | 0 | 879 | 831 | 1726 | 1631 | 949 | 1021 | 1494 |
| Hou | 701 | 940 | 879 | 0 | 1374 | 968 | 1420 | 1645 | 1891 | 1220 |
| LA | 1936 | 1745 | 831 | 1374 | 0 | 2339 | 2451 | 347 | 959 | 2300 |
| Mia | 604 | 1188 | 1726 | 968 | 2339 | 0 | 1092 | 2594 | 2734 | 923 |
| NY | 748 | 713 | 1631 | 1420 | 2451 | 1092 | 0 | 2571 | 2408 | 205 |
| SF | 2139 | 1858 | 949 | 1645 | 347 | 2594 | 2571 | 0 | 678 | 2442 |
| Sea | 2182 | 1737 | 1021 | 1891 | 959 | 2734 | 2408 | 678 | 0 | 2329 |
| DC | 543 | 597 | 1494 | 1220 | 2300 | 923 | 205 | 2442 | 2329 | 0 |
Ces données sont enregistrées au format .csv d'Excel dans le fichier : FlyingMileage.csv avec la structure indiquée ci-dessus.
On peut les charger dans R à l'aide de la commande :
distances <- read.csv2(file.choose())
en sélectionnant le fichier FlyingMileage.csv à l'aide de la fenêtre de dialogue qui s'affiche.
On utiise ensuite la commande smacofSym() qui se trouve dans le package smacof :
> library(smacof)
> res <- smacofSym(distances[,2:11])
> res
Call: smacofSym(delta = distances[, 2:11])
Model: Symmetric SMACOF
Number of objects: 10
Metric stress: 2.924599e-06
Number of iterations: 37
> res$conf
D1 D2
1 -0.45111770 0.10475917
2 -0.24870239 -0.20785555
3 0.30413799 -0.02472928
4 -0.09063497 0.36568699
5 0.76928208 0.21714502
6 -0.70471547 0.38884728
7 -0.68899029 -0.30427573
8 0.90028037 0.03897161
9 0.83680779 -0.38773602
10 -0.62634740 -0.19081348
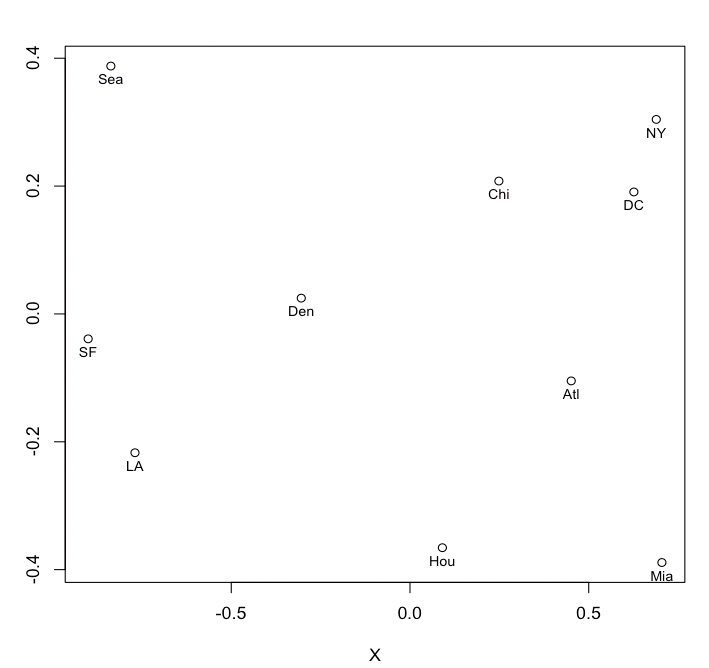
On change de signe les coordonnées sur les deux axes, afin d'avoir la "carte" orientée selon l'habitude
> Y <- -res$conf[,2]
> X <- -res$conf[,1]
> plot(X,Y,type="p")
> text(X,Y,distances[,1],pos=1,cex=0.8)
>
On obtient alors le graphe suivant :

Remarques. Le stress observé est évidemment très faible, puisque les données initiales sont (presque) des distances euclidiennes entre les objets. On remarque cependant que la solution obtenue est très différente de la solution fournie par le MDS classique, c'est-à-dire la procédure R cmdscale(). Les proximités ont subi ici une mise à l'échelle et les coordonnées s'expiment dans des intervalles complètement différents. Enfin, les positions mutuelles des points sont proches de celles fournies par cmdscale(), sans être parfaitement identiques.
Exemple 2
Enoncé :
Source : WICKELMAIER Florian, An Introduction to MDS, Sound Quality Research Unit, Aalborg University, Denmark
On demande à des sujets d'évaluer la similitude entre 12 sons de l'environnement courant.
Les données se présentent sous la forme suivante :
| Sound |
cs
|
dd
|
fa
|
ho
|
hw
|
sh
|
st
|
sw
|
tw
|
tg
|
wa
|
wf
|
|
| circular-saw |
cs
|
0
|
1
|
4
|
5
|
3
|
4
|
2
|
8
|
8
|
5
|
7
|
1
|
| dentist-s-drill |
dd
|
1
|
0
|
3
|
8
|
2
|
6
|
2
|
7
|
8
|
8
|
7
|
2
|
| fan |
fa
|
4
|
3
|
0
|
7
|
2
|
3
|
3
|
7
|
8
|
6
|
4
|
3
|
| hooves |
ho
|
5
|
8
|
7
|
0
|
8
|
9
|
3
|
8
|
2
|
2
|
9
|
5
|
| howling-wind |
hw
|
3
|
2
|
2
|
8
|
0
|
6
|
4
|
8
|
9
|
6
|
4
|
2
|
| ship-s-horn |
sh
|
4
|
6
|
3
|
9
|
6
|
0
|
1
|
3
|
9
|
8
|
5
|
3
|
| stadium |
st
|
2
|
2
|
3
|
3
|
4
|
1
|
0
|
4
|
3
|
6
|
7
|
1
|
| stone-in-well |
sw
|
8
|
7
|
7
|
8
|
8
|
3
|
4
|
0
|
9
|
6
|
9
|
5
|
| typewriter |
tw
|
8
|
8
|
8
|
2
|
9
|
9
|
3
|
9
|
0
|
4
|
9
|
9
|
| tire-on-gravel |
tg
|
5
|
8
|
6
|
2
|
6
|
8
|
6
|
6
|
4
|
0
|
4
|
3
|
| wasp |
wa
|
7
|
7
|
4
|
9
|
4
|
5
|
7
|
9
|
9
|
4
|
0
|
6
|
| waterfall |
wf
|
1
|
2
|
3
|
5
|
2
|
3
|
1
|
5
|
9
|
3
|
6
|
0
|
Ces données sont enregistrées au format .csv d'Excel dans le fichier Sounds.csv avec la structure indiquée ci-dessus.
On peut les charger dans R à l'aide de la commande :
> proxim <- read.csv2("Sounds.csv")
ou
> proxim <- read.csv2(file.choose())
et en sélectionnant le fichier Sounds.csv
N.B. read.csv2 permet de lire des données au format "table", avec les spécifications par défaut suivantes : séparateur = ";", séparateur décimal = ",".
On se limite aux données numériques :
> prox <- proxim[,3:14]
On utilise la commande smacofSym, qui se trouve dans le package smacof pour obtenir les coordonnées de la solution et le stress associé :
> library(smacof)
Le chargement a nécessité le package : polynom
Le chargement a nécessité le package : rgl
Le chargement a nécessité le package : scatterplot3d
> proxim
X Sound.no. cs dd fa ho hw sh st sw tw tg wa wf
1 circular-saw cs 0 1 4 5 3 4 2 8 8 5 7 1
2 dentist-s-drill dd 1 0 3 8 2 6 2 7 8 8 7 2
3 fan fa 4 3 0 7 2 3 3 7 8 6 4 3
4 hooves ho 5 8 7 0 8 9 3 8 2 2 9 5
5 howling-wind hw 3 2 2 8 0 6 4 8 9 6 4 2
6 ship-s-horn sh 4 6 3 9 6 0 1 3 9 8 5 3
7 stadium st 2 2 3 3 4 1 0 4 3 6 7 1
8 stone-in-well sw 8 7 7 8 8 3 4 0 9 6 9 5
9 typewriter tw 8 8 8 2 9 9 3 9 0 4 9 9
10 tire-on-gravel tg 5 8 6 2 6 8 6 6 4 0 4 3
11 wasp wa 7 7 4 9 4 5 7 9 9 4 0 6
12 waterfall wf 1 2 3 5 2 3 1 5 9 3 6 0
> prox <- proxim[,3:14]
> res <- smacofSym(prox)
> res
Call: smacofSym(delta = prox)
Model: Symmetric SMACOF
Number of objects: 12
Metric stress: 0.04252975
Number of iterations: 59
> res$conf
D1 D2
1 -0.316443823 0.043899870
2 -0.580117123 -0.011021816
3 -0.319950969 -0.302683196
4 0.779224961 0.008496235
5 -0.514904183 -0.352832685
6 -0.337999443 0.527879284
7 -0.004559679 0.228059144
8 0.004383611 0.940823320
9 1.032622044 0.064686472
10 0.550002329 -0.316146865
11 -0.111204095 -0.886161788
12 -0.181053630 0.055002026
> X <- res$conf[,1]
> Y <- res$conf[,2]
> plot(X,Y,type="p")
> text(X,Y,distances[,1],pos=1,cex=0.8)
Erreur dans as.graphicsAnnot(labels) : objet 'distances' introuvable
> text(X,Y,proxim[,2],pos=1,cex=0.8)
Résultat obtenu :
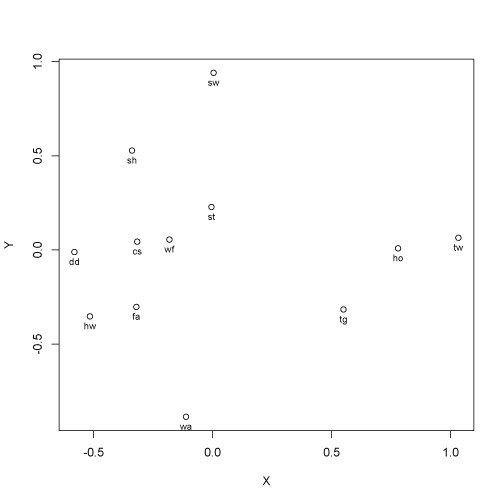
On pourra comparer ce graphique avec celui obtenu par un MDS non métrique (isoMDS() ou sammon()). Le résultat est assez nettement différent.