Sources :
WICKELMAIER Florian, An Introduction to MDS, Sound Quality Research Unit, Aalborg University, Denmark
PALM, R. , LE POSITIONNEMENT MULTIDIMENSIONNEL: PRINCIPES ET APPLICATION
L'algorithme INDSCAL est une extension de l'algorithme du MDS non métrique. Cette méthode, encore appelée Individual Difference Scaling ou weighted MDS (positionnement multidimensionnel pondéré) a été proposée par Carrol et Chang en 1970.
Principe mathématique :
Dans le MDS non métrique, les données sont constituées par une matrice de proximités (pij) entre n objets. Ici, on dispose d'une matrice de proximités par individu statistique (par exemple, par sujet, ou par instant d'observation).
On applique d'abord l'algorithme MDS à la matrice des données moyennes observées sur l'ensemble des individus. On obtient ainsi la représentation du MDS agrégé des différentes observations. On peut utiliser le MDS métrique ou non métrique.
On fait l'hypothèse que les individus statistiques utilisent tous les mêmes dimensions lorsqu'ils évaluent les objets, mais qu'ils peuvent appliquer des poids variables à ces dimensions. En estimant ces poids individuels et en les représentant graphiquement, on peut détecter différents groupes de sujets.
Ainsi, désignons par :
x_ik. la coordonnée de l'objet i sur l'axe k pour le MDS agrégé
x_ikl la coordonnée de l'objet i sur l'axe k pour le MDS du sujet l.
On a alors, pour le sujet l :
x_ikl = sqrt(w_kl) x_ik.
(d_ijl)^2 = somme(w_kl (x_ik. - x_jk.)^2)
Chaque individu est représenté dans l'espace des sujets, ou espace des poids, par ses poids sur chacune des dimensions.
Le package smacof comprend la procédure smacofIndDiff() qui fournit des méthodes voisines de celle de l'algorithme INDSCAL. Cette procédure prend en entrée une liste de matrices de dissimilarités et implémente différentes méthodes : null, identity, diagonal, idioscal.
Donnons un aperçu de cette méthode sur le mini-exemple fourni dans Doise, W et al., Représentations sociales et analyses de données, PUG, Grenoble, 1992 :
Six sujets doivent indiquer (par 1 ou 0) les similitudes entre 6 activités cognitives : Penser, S'informer, Décider, Organiser, Rêver, Imaginer (P, S, D, O, R, I). Les observations (matrices de co-occurrences) sont les suivantes :
Sujet 1
| P | S | D | O | R | I |
| 1 | 1 | 0 | 0 | 0 | 0 |
| 1 | 1 | 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 1 | 0 | 0 |
| 0 | 0 | 1 | 1 | 0 | 0 |
| 0 | 0 | 0 | 0 | 1 | 1 |
| 0 | 0 | 0 | 0 | 1 | 1 |
Sujet 2
| P | S | D | O | R | I |
| 1 | 1 | 1 | 0 | 0 | 0 |
| 1 | 1 | 1 | 0 | 0 | 0 |
| 1 | 1 | 1 | 0 | 0 | 0 |
| 0 | 0 | 0 | 1 | 1 | 1 |
| 0 | 0 | 0 | 1 | 1 | 1 |
| 0 | 0 | 0 | 1 | 1 | 1 |
Sujet 3
| P | S | D | O | R | I |
| 1 | 0 | 0 | 1 | 0 | 0 |
| 0 | 1 | 0 | 0 | 1 | 0 |
| 0 | 0 | 1 | 0 | 0 | 1 |
| 1 | 0 | 0 | 1 | 0 | 0 |
| 0 | 1 | 0 | 0 | 1 | 0 |
| 0 | 0 | 1 | 0 | 0 | 1 |
Sujet 4
| P | S | D | O | R | I |
| 1 | 1 | 1 | 0 | 0 | 0 |
| 1 | 1 | 1 | 0 | 0 | 0 |
| 1 | 1 | 1 | 0 | 0 | 0 |
| 0 | 0 | 0 | 1 | 0 | 1 |
| 0 | 0 | 0 | 0 | 1 | 0 |
| 0 | 0 | 0 | 1 | 0 | 1 |
Sujet 5
| P | S | D | O | R | I |
| 1 | 0 | 0 | 1 | 0 | 0 |
| 0 | 1 | 1 | 0 | 0 | 0 |
| 0 | 1 | 1 | 0 | 0 | 0 |
| 1 | 0 | 0 | 1 | 0 | 0 |
| 0 | 0 | 0 | 0 | 1 | 1 |
| 0 | 0 | 0 | 0 | 1 | 1 |
Sujet 6
| P | S | D | O | R | I |
| 1 | 1 | 1 | 1 | 0 | 0 |
| 1 | 1 | 1 | 1 | 0 | 0 |
| 1 | 1 | 1 | 1 | 0 | 0 |
| 0 | 0 | 0 | 1 | 0 | 0 |
| 0 | 0 | 0 | 0 | 1 | 1 |
| 0 | 0 | 0 | 0 | 1 | 1 |
N.B. Les noms des lignes (P, S, D, O, R, I) n'ont pas été indiqués.
Ces données sont disponibles dans le classeur Excel Indscal-Doise.xls , ou dans les 6 fichiers i1.csv, i2.csv, i3.csv, i4.csv, i5.csv, i6.csv.
On peut les importer dans R par :
> i1 <- read.csv2(file.choose()) # choisir i1.csv
> i2 <- read.csv2(file.choose()) # choisir i2.csv
> i3 <- read.csv2(file.choose()) # choisir i3.csv
> i4 <- read.csv2(file.choose()) # choisir i4.csv
> i5 <- read.csv2(file.choose()) # choisir i5.csv
> i6 <- read.csv2(file.choose()) # choisir i6.csv
On transforme ensuite ces matrices de similarités en dissimilarités par :
> j1 <- 1 - i1
> j2 <- 1 - i2
> j3 <- 1 - i3
> j4 <- 1 - i4
> j5 <- 1 - i5
> j6 <- 1 - i6
Enfin, on forme une liste de matrices :
> j <- list(j1,j2,j3,j4,j5,j6)
On appelle la méthode "diagonal" dans la procédure smacofIndDiff() du package smacof (par défaut, la solution sera obtenue en dimension 2) :
library(smacof)
result.diag <- smacofIndDiff(j, constraint="diagonal")
On peut ainsi obtenir :
- les matrices des dissimilarités observées , normalisées :
> result.diag$obsdiss
[[1]]
1 2 3 4 5
2 0.000000
3 1.118034 1.118034
4 1.118034 1.118034 0.000000
5 1.118034 1.118034 1.118034 1.118034
6 1.118034 1.118034 1.118034 1.118034 0.000000
[[2]]
1 2 3 4 5
2 0.000000
3 0.000000 0.000000
4 1.290994 1.290994 1.290994
5 1.290994 1.290994 1.290994 0.000000
6 1.290994 1.290994 1.290994 0.000000 0.000000
[[3]]
1 2 3 4 5
2 1.118034
3 1.118034 1.118034
4 0.000000 1.118034 1.118034
5 1.118034 0.000000 1.118034 1.118034
6 1.118034 1.118034 0.000000 1.118034 1.118034
[[4]]
1 2 3 4 5
2 0.000000
3 0.000000 0.000000
4 1.167748 1.167748 1.167748
5 1.167748 1.167748 1.167748 1.167748
6 1.167748 1.167748 1.167748 0.000000 1.167748
[[5]]
1 2 3 4 5
2 1.118034
3 1.118034 0.000000
4 0.000000 1.118034 1.118034
5 1.118034 1.118034 1.118034 1.118034
6 1.118034 1.118034 1.118034 1.118034 0.000000
[[6]]
1 2 3 4 5
2 0.000000
3 0.000000 0.000000
4 1.167748 1.167748 1.167748
5 1.167748 1.167748 1.167748 1.167748
6 1.167748 1.167748 1.167748 1.167748 0.000000
- la liste des dissimilarités, pour la configuration obtenue :
> result.diag$confdiss
[[1]]
1 2 3 4 5
2 0.8375350
3 0.4819336 0.3556170
4 0.9069197 1.3315281 1.0924866
5 1.3957490 1.0770208 1.1479602 1.0536146
6 1.2106049 1.1509109 1.0988739 0.6835261 0.3871911
[[2]]
1 2 3 4 5
2 0.04767051
3 0.02426873 0.02340178
4 1.12987058 1.17754109 1.15413931
5 1.29782330 1.34549381 1.32209203 0.16795272
6 1.35167465 1.39934516 1.37594338 0.22180407 0.05385135
[[3]]
1 2 3 4 5
2 1.3851753
3 0.7972347 0.5879405
4 0.1787154 1.5638414 0.9759046
5 1.5515543 0.1664561 0.7543292 1.7302050
6 0.9144874 0.4707363 0.1173640 1.0931312 0.6370740
[[4]]
1 2 3 4 5
2 0.5245606
3 0.3016771 0.2229169
4 1.0485098 1.2399189 1.1304767
5 1.3368970 1.2476031 1.2570026 0.6711682
6 1.2984407 1.3080089 1.2749887 0.4608087 0.2455198
[[5]]
1 2 3 4 5
2 1.0140950
3 0.5835951 0.4305093
4 0.7811377 1.3977197 1.0624327
5 1.4392523 0.9251343 1.0567414 1.2712079
6 1.1386637 1.0140783 0.9417593 0.8140385 0.4676090
[[6]]
1 2 3 4 5
2 0.5898576
3 0.3392935 0.2505925
4 1.0257252 1.2560293 1.1240828
5 1.3471248 1.2201744 1.2390689 0.7503762
6 1.2838728 1.2825555 1.2466887 0.5058151 0.2749194
- la liste des coordonnées des points de la configuration finale, pour les 6 sujets :
> result.diag$conf
[[1]]
D1 D2
1 -0.4365826 -0.39892006
2 -0.4702644 0.34282872
3 -0.4537298 0.02799191
4 0.3617310 -0.49459040
5 0.4803985 0.43191859
6 0.5184473 0.09077125
[[2]]
D1 D2
1 -0.6144467 -3.840544e-25
2 -0.6618504 3.300533e-25
3 -0.6385796 2.694879e-26
4 0.5091004 -4.761596e-25
5 0.6761132 4.158232e-25
6 0.7296632 8.738867e-26
[[3]]
D1 D2
1 -0.002277144 -0.69194523
2 -0.002452823 0.59465222
3 -0.002366581 0.04855325
4 0.001886730 -0.85788984
5 0.002505681 0.74918269
6 0.002704137 0.15744691
[[4]]
D1 D2
1 -0.5371782 -0.26389663
2 -0.5786207 0.22679066
3 -0.5582763 0.01851742
4 0.4450795 -0.32718519
5 0.5910899 0.28572606
6 0.6379058 0.06004768
[[5]]
D1 D2
1 -0.3973793 -0.51432563
2 -0.4280365 0.44200735
3 -0.4129867 0.03608982
4 0.3292490 -0.63767292
5 0.4372606 0.55687047
6 0.4718928 0.11703091
[[6]]
D1 D2
1 -0.5348628 -0.30249666
2 -0.5761268 0.25996322
3 -0.5558700 0.02122595
4 0.4431611 -0.37504242
5 0.5885422 0.32751908
6 0.6351563 0.06883083
- la matrice des coordonnées des points représentant les 6 objets, dans l'espace global :
> result.diag$gspace
D1 D2
1 -0.4642525 -0.38121748
2 -0.5000689 0.32761526
3 -0.4824864 0.02674973
4 0.3846568 -0.47264232
5 0.5108453 0.41275165
6 0.5513056 0.08674316
- Les matrices représentant les poids des individus : si on note Xi la matrice des coordonnées des points dans l'espace de l'individu i, X celle des coordonnées des points dans l'espace commun et Wi la matrice des poids correspondant à l'individu i, on a : Xi = X * Wi. La méthode "diagonal" produit des matrices diagonales pour les poids. La méthode "idioscal" produit des matrices quelconques.
> result.diag$cweights
[[1]]
D1 D2
D1 0.9403991 0.000000
D2 0.0000000 1.046437
[[2]]
D1 D2
D1 1.323518 0.000000e+00
D2 0.000000 1.007442e-24
[[3]]
D1 D2
D1 0.00490497 0.000000
D2 0.00000000 1.815093
[[4]]
D1 D2
D1 1.157082 0.0000000
D2 0.000000 0.6922469
[[5]]
D1 D2
D1 0.855955 0.000000
D2 0.000000 1.349166
[[6]]
D1 D2
D1 1.152095 0.0000000
D2 0.000000 0.7935016
- Le stress global (ici, assez mauvais) :
> result.diag$stress.m
[1] 0.6768095
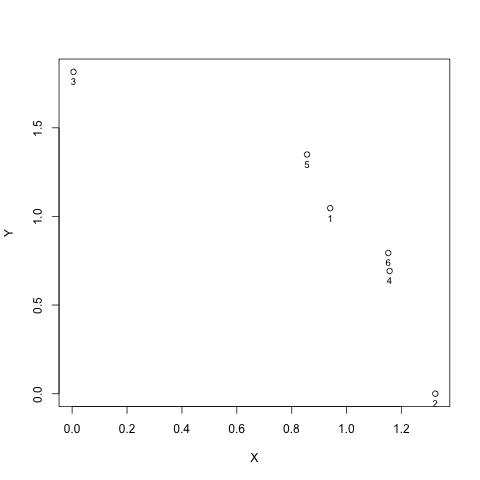
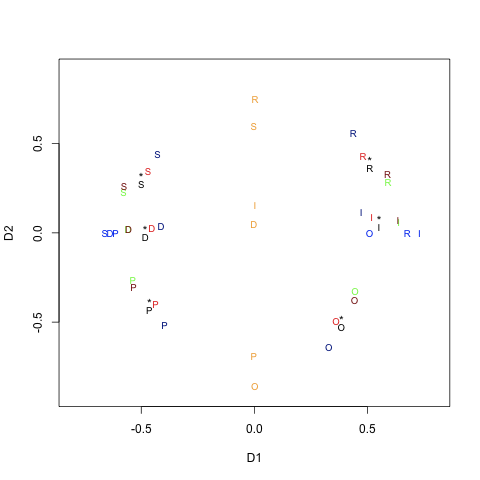
On voit ici, par exemple, que la première dimension oppose P, S, D à O, R, I. L'individu 2 a un poids fort sur cette dimension et un poids pratiquement nul sur la seconde. Il a justement choisi les regroupements [PSD] et [ORI]. Les sujets 4 et 6 ont également des poids forts sur cette dimension : ils ont regroupé [PSD] mais diffèrent (et diffèrent du sujet 2) sur les regroupements de O, R et I.
La configuration finale peut être représentée sur le graphique suivant, dans lequel les espaces des différents sujets ont été distingués par un jeu de couleurs et la position des objets dans l'espace commun est reportée par des "*", avec des légendes en noir.
plot(result.diag$gspace,xlim=c(-.8,.8),ylim=c(-.9,.9),pch="*")
text(result.diag$gspace,c("P","S","D","O","R","I"),pos=1,cex=.8, col="black")
text(result.diag$conf[[1]],c("P","S","D","O","R","I"),cex=.8, col="red")
text(result.diag$conf[[2]],c("P","S","D","O","R","I"),cex=.8, col="blue")
text(result.diag$conf[[3]],c("P","S","D","O","R","I"),cex=.8, col="orange")
text(result.diag$conf[[4]],c("P","S","D","O","R","I"),cex=.8, col="green")
text(result.diag$conf[[5]],c("P","S","D","O","R","I"),cex=.8, col="dark blue")
text(result.diag$conf[[6]],c("P","S","D","O","R","I"),cex=.8, col="dark red")

Les poids des individus peuvent être représentés par :
X <- c(result.diag$cweights[[1]][1,1],result.diag$cweights[[2]][1,1],result.diag$cweights[[3]][1,1],result.diag$cweights[[4]][1,1],result.diag$cweights[[5]][1,1],result.diag$cweights[[6]][1,1])
Y <- c(result.diag$cweights[[1]][2,2],result.diag$cweights[[2]][2,2],result.diag$cweights[[3]][2,2],result.diag$cweights[[4]][2,2],result.diag$cweights[[5]][2,2],result.diag$cweights[[6]][2,2])
plot(X,Y)
text(X,Y,c("1","2","3","4","5","6"),pos=1, cex=.8)