SMS Spring Meeting 2024

Participants

---

• Olivier Benoist (Paris)
• Thomas Blomme (Neuchâtel)
• Francesca Carocci (Geneva)
• Alois Demory (Paris)
• Ilia Itenberg (Paris)
• Andres Jaramillo Puentes (Essen)
• Hannah Markwig (Tübingen)
• Gurvan Mével (Nantes)
• Grigory Mikhalkin (Geneva)
• Victoria Schleis (Tübingen)
• Antoine Toussaint (Geneva)

Schedule

---

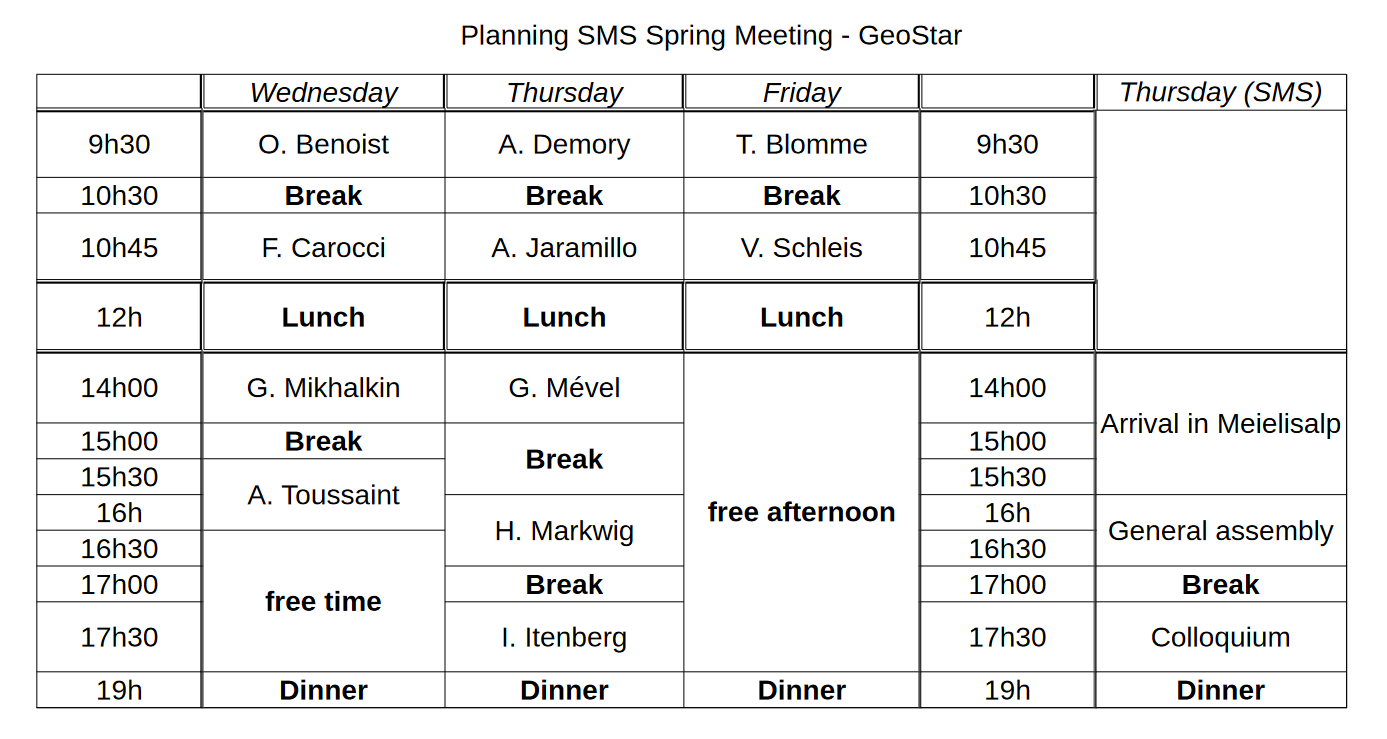
Abstracts

---

O. Benoist - The Wu relations in real algebraic geometry.

---

I will describe and study relations between Chern classes and Galois cohomology classes in the Gal(C/R)-equivariant cohomology of real algebraic varieties with no real points. These relations have applications to sums of squares problems, in the spirit of Hilbert's 17th problem. For instance, one can use them to show that a nonnegative real polynomial in R[X_1,...,X_n] of degree at most n-1 is a sum of 2^{n-1} squares in the field R(X_1,...,X_n) of rational functions. This is joint work with Olivier Wittenberg.

T. Blomme - A signed count to bitangents to a real plane curve.

---

In 1834, Plücker computed the number of flexes and bitangents to a plane complex curve of degree d, which do not depend on the choice of the curve povided it is generic. The situation in the real case, first studied by Zeuthen in the case of quartic curves, is more delicate. In this talk, we will prove the existence of a signed count of the real bitangents to a plane curve of even degree that only depend on the topology of the pair (RC,RP²). This is a joint work with E. Brugallé and Cristhian Garay.

F. Carocci - A logarithmic approach to linear series.

---

Maps to projective space are given by basepoint-free linear series, thus these are key to understanding the extrinsic geometry of algebraic curves. How does a linear series degenerate when the underlying curve degenerates and becomes nodal ? Eisenbud and Harris gave a satisfactory answer to this question when the nodal curve is of compact type. I will report on a joint work in progress with Luca Battistella and Jonathan Wise, in which we review this question from a moduli-theoretic and logarithmic perspective. The logarithmic prospective helps understanding the rich polyhedral and combinatorial structures underlying degenerations of linear series; these are linked with the theory of matroids and Bruhat–Tits buildings.

A. Demory - Topology of three- and four-dimensional maximal real structures on double coverings ramified along maximal real algebraic hypersurfaces.

---

The study of the topological properties of real algebraic varieties, i.e. complex algebraic varieties endowed with an antiholomorphic involution, is a problem that can be traced back to the work of A. Harnack and D. Hilbert on real algebraic plane curves at the end of the 19th century. Nowadays, we are particularly interested in the topology of maximal real algebraic varieties, for which the homology of the fixed points set of the involution is as rich as possible. However, there are very few known examples of maximal real algebraic varieties of dimension 3 and higher. In this talk, we contribute to filling this gap by studying three- and four-dimensional maximal real algebraic varieties obtained by considering double coverings of projective spaces and quadric hypersurfaces ramified along maximal real algebraic hypersurfaces, and endowed with involutions obtained by lifting the involution of the basis.

I. Itenberg - Refined invariants for real curves.

---

The talk is devoted to several real and tropical enumerative problems. We suggest new invariants of the projective plane (and, more generally, of certain toric surfaces) that arise from appropriate enumeration of real algebraic curves of genus 1 and 2. These invariants admit a refinement (according to the quantum index) similar to the one introduced by Grigory Mikhalkin in the genus zero case. We also discuss the tropical counterparts of the invariants under consideration and establish a tropical algorithm allowing one to compute them. This is a joint work with Eugenii Shustin.

A. Jaramillo - Motivic Gromov-Witten invariants.

---

Over the complex numbers the solutions to enumerative problems are invariant: the number of solutions of a polynomial equation or polynomial system, the number of lines or curves in a surface, etc. Over the real numbers such invariance fails. However, the signed count of solutions may lead to numerical invariants: Descartes' rule of signs, Poincaré-Hopf theorem, real curve-counting invariants.
Since many of this problems have a geometric nature, one may ask the same problems for arbitrary fields. Motivic homotopy theory allows to do enumerative geometry over an arbitrary base, leading to additional arithmetic and geometric information.
The goal of this talk is to illustrate a generalized notion of sign that allows us to state a movitic version of the Gromov-Witten invariants, a correspondence theorem and a wall-crossing formula for quadratic field extensions.

H. Markwig - The moduli space of twisted canonical divisors and tropical leaky covers.

---

(Joint work with Renzo Cavalieri, Dhruv Ranganathan, Johannes Schmitt) The moduli space of twisted canonical divisors can be viewed as a variant of the Hurwitz space parametrizing genus g degree d covers of a line with two special ramification profiles fixed for 0 and infinity.
The Hurwitz space can be used to define the classical (double) Hurwitz numbers which count covers of Riemann surfaces satisfying fixed ramification data. There is a correspondence theorem showing that Hurwitz numbers can be determined by counting the analogous tropical covers. One can similarly define an intersection product on the moduli space of twisted canonical divisors, for which we prove that it equals a count of tropical covers which do not satisfy the balancing condition but leak at every vertex. We call these leaky tropical covers.
Properties of these leaky tropical covers can be studied with tropical methods.

G. Mével - Asymptotic computations of tropical refined invariants.

---

Tropical refined invariants are polynomial that interpolate between real and complex enumerations of curves on toric surfaces. Brugallé and Jaramillo-Puentes showed that, when the genus is fixed, their coefficients are asymptotically polynomial. This brings back Göttsche's conjecture in a dual (because the genus is fixed instead of the number of nodes) and refined (that's in the name :) ) setting. In this talk we investigate the generating series of these asymptotic polynomials in genus 1. We will not go into detailled computations, but we will explain the idea to pass from genus 0 to genus 1. This is joint work with Thomas Blomme.

G. Mikhalkin - Ellipsoid superpotentials: obstructing symplecting embeddings by singular algebraic curves.

---

How singular can be a local branch of a plane algebraic curve of a given degree d? A remarkable series of real algebraic curves was constructed by Stepan Orevkov. It is based on even-indexed numbers in the Fibonacci series: a degree 5 curve with a 13/2 cusp, a degree 13 curve with a 34/5-cusp, and so on. We discuss this and other series of algebraic curves in the context of the problem of symplectic packing of an ellipsoid into a ball, with the answer given by the spectacular "Fibonacci staircase" of McDuff and Schlenk. The aspect ratio a>1 of the ellipsoid can be viewed as a real parameter for a certain enumerative superpotential function, which is mostly locally constant, but jumps at certain specific rational values (responsible for the aspects of cusp singularities). Based on joint work with Kyler Siegel.

A. Toussaint - Real Structures of phase tropical hypersurfaces.

---

In this talk, phase tropical hypersurfaces are manifolds equivariantly homeomorphic to the complex part of a T-hypersurface obtained by primitive patchworking, which admits a stratified fibration onto the tropical hypersurface dual to the triangulation of the patchworking. By studying the real structures of these phase tropical hypersurfaces, we explain how to generalize the notion of twisted edges (which is well known in the case of curves since the work of B. Haas) to a T-hypersurface in any dimension and use it to lift the tropical homology to the homology of the phase tropical hypersurface. We will explain the connection with the first page of the Renaudineau-Shaw spectral sequence and some possible applications.

V. Schleis - Tropical curve counting on ruled surfaces.

---

We study the problem of counting curves on ruledsurfaces. To this end, we develop tools that allow us to count curves on non-orientable surfaces. For two of these surfaces, we establish a tropical curve countand prove its correspondence to the algebraic-geometric Gromov-Witten invariant. Further, we prove regularity results on the generating series of the Gromov-Witten invariants — weshow that they are quasi-polynomial and quasi-modular. This is joint work with Thomas Blomme.

How to Go to Meielisalp ?

---

The CFF/SBB app is your best friend ! Basically, you need to go to Spiez In Spiez, get out of the train station and take the bus B60 to Leissingen, where the hotel shuttle should wait for you. The bold ones may go by foot, which is approximately 25min walk.

If you are coming from Zürich, you have direct trains leaving at **h02 to Spiez but you may have to change in Bern.

If you are coming from Basel, take train at **h28 or **h56 going to Brig or Interlaken, and get out in Spiez.

If you are coming from Bern, take train at **h04 or **h34 going to Brig or Interlaken, and get out in Spiez.

If you are coming from Lausanne, you need to go to Bern first and change in Bern and follow the corresponding instructions.

Thomas Blomme (organizer)

---