Modélisation d'une interaction proie-prédateur

La dynamique des populations est une discipline qui suscite particulièrement la modélisation. Les données de terrain présentent parfois un aspect oscillatoire qui a été expliqué par une interaction entre proies et prédateurs. C'est le cas des fluctuations du nombre de lynx et de lièvres (estimé à partir du nombre de peaux de ces animaux rapportées par les trappeurs de la baie d'Hudson) et enregistrées par la compagnie de la baie d'Hudson pendant une centaine d'années.

Un article paru dans Nature (vol 405, p 562-565 (Juin 2000)) suggère, en se basant sur l'analyse statistique des effectifs de populations de rongeurs (lemmings et campagnols), que la forme des pics est liée au type de contrôle de la population. Les lemmings ont des pics "pointus", car leur effectif est contrôlé par la végétation qui leur sert de nourriture (type "prédateur"), alors que les campagnols ont des pics plus "plats", car leur effectif passe par une phase de saturation avant d'être diminué rapidement par la prédation, dont l'influence ne se fait sentir que tardivement (l'effectif des prédateurs ne croit sensiblement que si les proies sont assez nombreuses).
Je vais essayer de trouver une façon de modéliser l'interaction proie-prédateur qui puisse rendre compte de telles caractéristiques.

Mon modèle est en temps discret, ce qui pourrait correspondre à une réévaluation des effectifs tous les ans, et qui par ailleurs est facile à gérer avec le programme ULM (Unified Life Models).
Il comporte deux classes : les proies (d'effectif n), et les prédateurs (d'effectif p).

J'ai représenté la probabilité, pour une proie, de se faire manger par la fonction :
(2/pi)*atan(k*p*pi/(2*n))
où k est le nombre de proies qu'un prédateur mange quand il en trouve en abondance, c'est-à-dire quand p/n tend vers 0 ; en effet, au voisinage de 0, la fonction est équivalente à kp/n ; (nombre de proies mangées)/(nombre de proies).
Quand p/n tend vers l'infini, la fonction tend vers 1 : une proie a toutes les chances de se faire manger quand les prédateurs abondent.

J'ai représenté la mortalité des proies hors prédation par la fonction :
1-(1-mo)*exp(-vs*n)
où mo est la mortalité quand la densité des proies a une influence négligeable sur la survie. En effet, quand n tend vers 0, cette fonction tend vers mo (mortalité "naturelle"). (Ce n'est peut-être pas une fonction très appropriée ; il faudrait une fonction à pente nulle au voisinage de 0 ; sigmoïde).
vs représente une "vitesse" de saturation de la population de proies.
Quand la densité de proies est trop élevée, les conditions sont invivables : la limite quand n tend vers l'infini de cette mortalité est 1. Plus vs est élevée, plus rapidement on se rapproche de 1.

r représente la croissance de la population de proies (avant décompte des morts) : chaque année, chaque proie donne naissance à r-1 nouvelles proies en moyenne.

Il y a donc au début de chaque année, r*n proies, qui doivent survivre à la prédation (probabilité 1-(2/pi)*atan(k*p*pi/(2*n))) et aux autres causes de mortalité (probablité (1-mo)*exp(-vs*n)), il reste donc r*n*(1-(2/pi)*atan(k*p*pi/(2*n)))*(1-mo)*exp(-vs*n) proies à la fin de l'année.

La reproduction nette (naissances et survie) des prédateurs dépend des ressources disponibles, c'est-à-dire du nombre de proies mangées. Chaque prédateur dispose en moyenne de n*(2/pi)*atan(k*p*pi/(2*n))/p proies à manger chaque année, ce qui, après multiplication par un coefficient alpha de conversion des proies mangées en taux de reproduction nette, donne alpha*n*(2/pi)*atan(k*p*pi/(2*n))/p prédateurs à la fin de l'année pour un prédateur présent au début, soit en tout n*alpha*(2/pi)*atan(k*p*pi/(2*n)) prédateurs.

Par modifications successives des paramètres j'ai réussi à obtenir des oscillations, mais ces oscillations ne présentent pas la forme espérée : les proies ont des pics "pointus".

J'ai pensé qu'en séparant les prédateurs en deux classes, dont une seule serait capable de chasser et de se reproduire, les proies auraient le temps d'atteindre la saturation.
Il y a donc en tout trois classes : les proies (d'effectif n), les prédateurs juvéniles (p1), et les prédateurs adultes (p2).

Le principe est le même que dans le premier modèle, avec p2 jouant le rôle de p. J'ai cependant décomposé les calculs dans le programme, avec une fonction mange(n,p2) determinant la proportion de proies tuées, pour rendre le programme plus lisible et plus facilement modifiable. On a donc :
mange(n,p2)=(2/pi)*atan(k*p2*pi/(2*n))
où k est le nombre de proies qu'un prédateur adulte tue si les proies sont très abondantes.
Le nombre de proies mangées est nm = n*mange(n,p2).

J'ai décomposé le coefficient de conversion des proies mangées en trois parties.
Une fonction n2(n,p2)=if(p2<1,1,if(nm<(k2*p2),nm/(k2*p2),1)) représente le taux de satisfaction des besoins alimentaires des adultes, où k2 est le nombre de proies qu'un adulte doit manger pour être bien nourri. La satisfaction des besoins alimentaires des adultes est prioritaire sur celle des petits, représentée par la fonction n1(n,p1,p2)=if(p1<1,1,if(nm<(k2*p2),0,if(nm<(k2*p2+k1*p1),(nm-k2*p2)/(k1*p1),1)) où k1 est le nombre de proies qu'un juvénile doit manger pour être bien nourri.
Enfin, s'il reste des proies, les adultes peuvent les "convertir" en petits suivant la fonction de fécondité f(n,p1,p2)=if(p2<1,0,if(nm<(k2*p2+k1*p1),0,(nm-((k1*p1)+(k2*p2)))/(alpha*p2)))
où alpha est le nombre de proies qu'un adulte doit manger pour pouvoir donner naissance à un petit.
Les proies tuées sont donc "converties", par ordre de priorité :
- en nourriture pour les besoins alimentaires de base des adultes,
- en nourriture pour les juvéniles,
- et en nouveaux-nés, via une augmentation des ressources des adultes.
Pour éviter des problèmes de divisions par zéro, j'ai dû attribuer des survies et fécondités dans les cas où il n'y a pas de prédateurs.

Il y a par ailleurs une mortalité autre que celle dûe à la malnutrition (dite "dûe aux accidents") : m1 pour les juvéniles et m2 pour les adultes.

Les juvéniles de l'année en cours sont issus de la reproduction des adultes de l'année précédente, il y en a donc p2*f(n,p1,p2).

Les adultes de l'année en cours sont ceux de l'année précédente qui ont suvécu aux "accidents" et qui ont été bien nourris ainsi que les juvéniles qui ont survécu et grandi.
Il y a donc en tout p1*(1-m1)*n1(n,p1,p2) + p2*(1-m2)*n2(n,p2) adultes.

Après modifications successives des paramètres, j'ai obtenu des oscillations. Il pourrait sembler que la courbe des proies présente un début d'applatissement avant de chuter. Cette impression est peut-être liée à la rapidité d'évolution des effectifs (il n'y a pas de points intermédiaires). De plus, il est clair que la prédation n'est pas du tout négligeable lors de cette éventuelle pseudo-saturation (comparer la hauteur des  pics pendant les oscillations avec l'effectif atteint avant que les prédateurs n'aient eu le temps de se multiplier sensiblement).

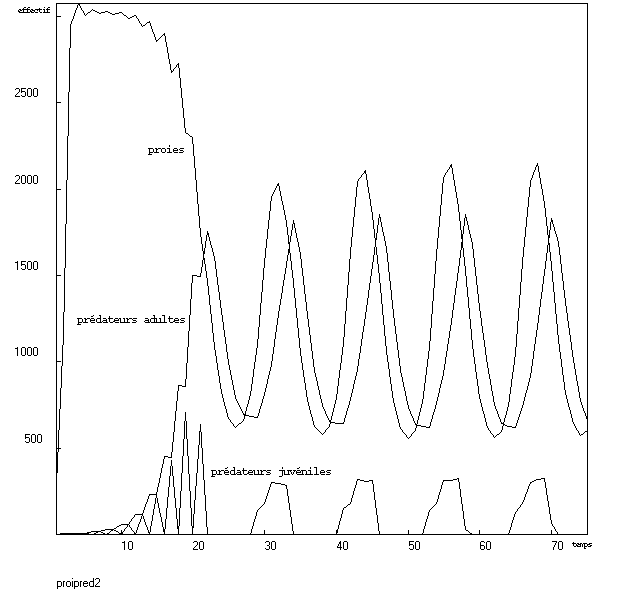
Dans l'article de Nature, il y avait une représentation avec échelle logarithmique qui faisait ressortir l'applatissement de la courbe des proies. Si l'on compare les deux résultats de la modélisation selon ce mode de représentation, la saturation chez les proies est encore moins visible. Essayons donc avec une autre fonction de densité-dépendance (fonction responsable de la saturation de l'effectif des proies).

Le modèle est le même que précédemment, sauf pour la survie des proies.
La probabilité de survie des proies aux événements autres que la prédation est maintenant de : (1-mo)*exp(-vs*n*n).

Après ajustement des paramètres, on obtient la courbe suivante :

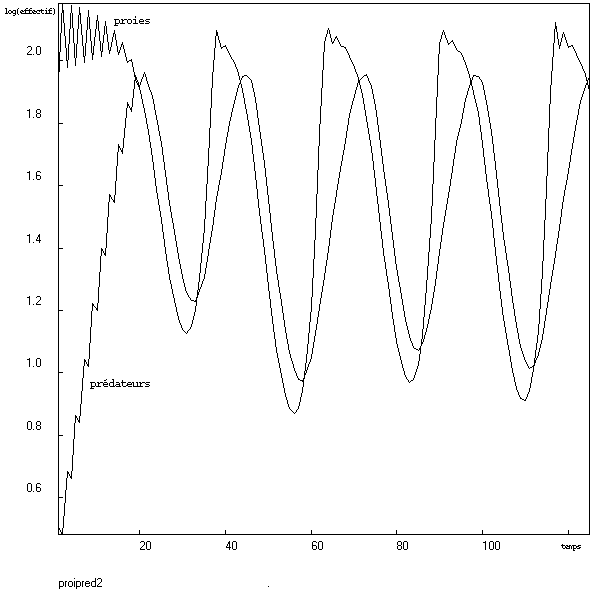
Il semble bien que l'effectif des proies atteigne la saturation avant de diminuer sous l'effet de la prédation.
La "réussite" de ce modèle tient elle dans la nouvelle fonction de densité-dépendance, où dans un meilleur ajustement des paramètres ? Il est possible que la fonction de densité-dépendance de ce modèle facilite l'ajustement des paramètres. Quoi qu'il en soit, l'article de Nature présente une courbe où la saturation est atteinte progressivement, ce qui n'est pas le cas ici, de plus l'effectif des proies oscille assez fortement à saturation. Ceci est peut-être dû au fait que mon modèle est en temps discret.

J'ai obtenu un modèle de dynamique proies-prédateurs qui oscille régulièrement, avec saturation des proies lors du pic de celles-ci. J'ai obtenu ces résultats par modifications successives du modèle. Il serait bon de prévoir à l'avance par le calcul certaines propriétés des courbes obtenues pour un modèle donné, comme les conditions d'existence d'oscillations et d'une phase de saturation pour les proies. L'ajustement des paramètres est en effet une phase du travail qui demande du temps (surtout au début, quand on n'a pas encore bien pris conscience des influences des différents paramètres).
On aurait pu aussi essayer de trouver un modèle en temps continu.